来自 _Scientific American_ 的螺栓谜题

And now it’s all this
I just said what I said and it was wrong Or was taken wrong
A SciAm bolt puzzle
2025年3月3日上午6:26,Dr. Drang 发布
大约一周前,Scientific American 重新发布了 Martin Gardner 在 1958 年提出的这个谜题:
将两个相同的螺栓放在一起,使它们的螺旋槽相互啮合(见图)。 如果你像拨弄拇指一样移动这些螺栓,用手牢牢地握住每个螺栓的头部,使其不旋转,那么螺栓头会向内移动,向外移动,还是与彼此保持相同的距离? 当然,这个问题应该在不借助实际测试的情况下解决。
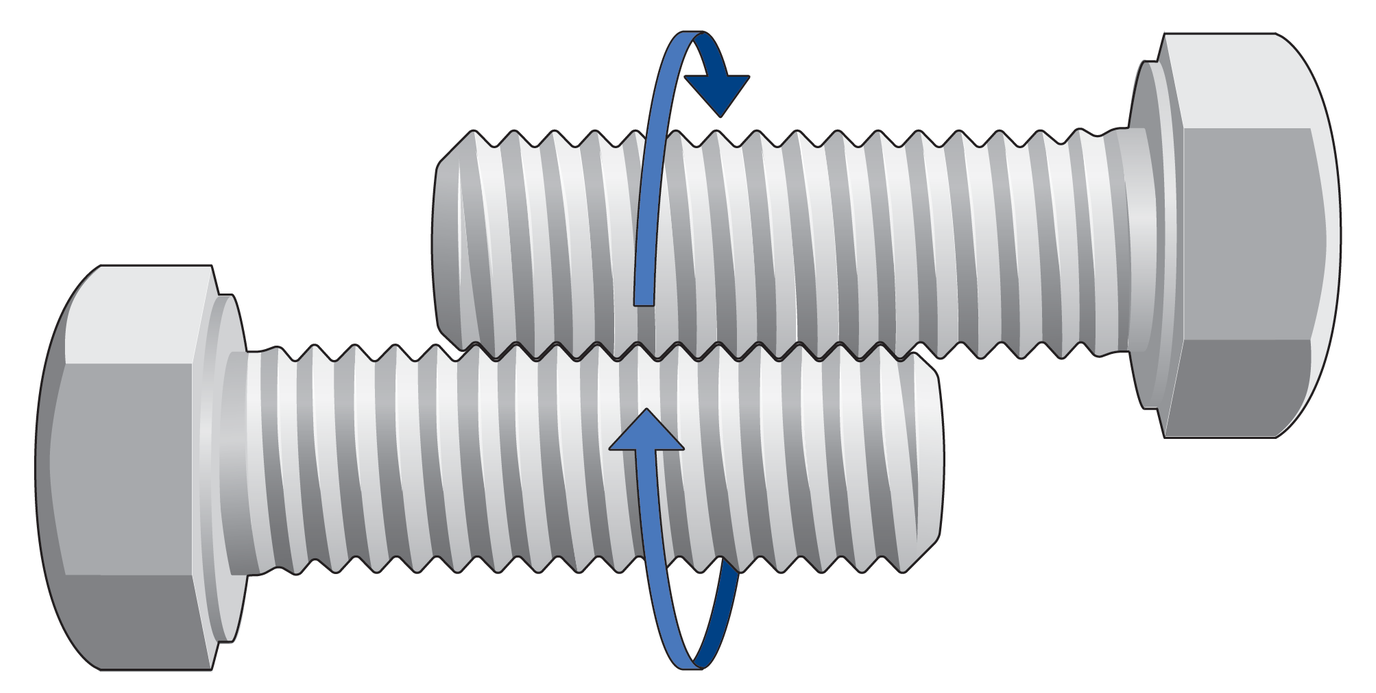
Scientific American 的 Amanda Montañez 绘制的插图。
“拨弄拇指”的描述非常好。因为螺栓运动的一个关键特征是,即使它们相互环绕,它们也 不 旋转。 例如,它们头部上的垂直面在整个运动过程中始终保持垂直。
同样重要的是,螺栓是相同的,否则它们的螺纹不会啮合。 这是来自 ANSI Standard ASME B1.1,《Unified Inch Screw Threads》(统一英寸螺纹)的标准螺纹轮廓图:
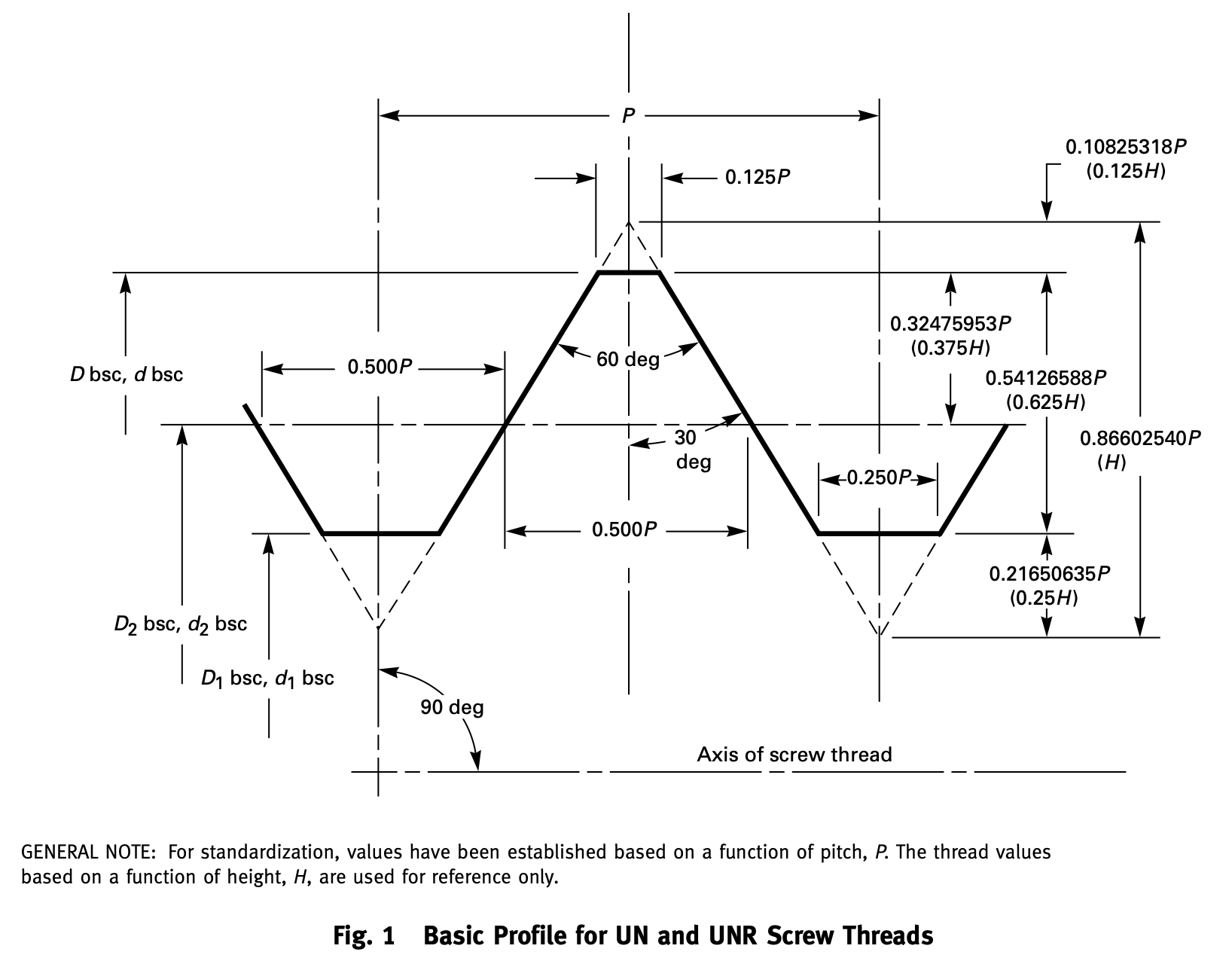
如果两个螺栓的螺距 P、大径 D 和小径 D1 相匹配(只有当螺栓相同时才会匹配),则螺栓将紧密配合,并且可以相互滑动而不会卡住。 如果尺寸不匹配,则螺栓将无法配合在一起。
(顺便说一句,虽然 B1.1 标准适用于以英寸为单位测量的螺纹,但此螺纹轮廓也适用于公制螺纹。 区别在于公制螺纹的螺距和直径将以毫米为单位给出。)
Gardner 的答案是:
拨弄的螺栓的头部既不向内也不向外移动。 这种情况类似于一个人以与自动扶梯向下移动的速度相同的速度向上行走。
这当然是真的,但我发现这个类比没有特别的帮助。 为什么拨弄螺栓就像一个人走上自动扶梯? 人和自动扶梯是两个非常不同的事物,但两个螺栓是相同的。
让我们仔细看看几何形状。 这是两个螺栓的程式化图。 螺纹峰的中心绘制为黑色螺旋线; 螺纹谷的中心绘制为蓝色螺旋线; 螺杆绘制为半透明圆柱体,因此您可以看到螺栓相对侧的螺纹。 我省略了螺栓头,因为它们在啮合中没有任何作用。
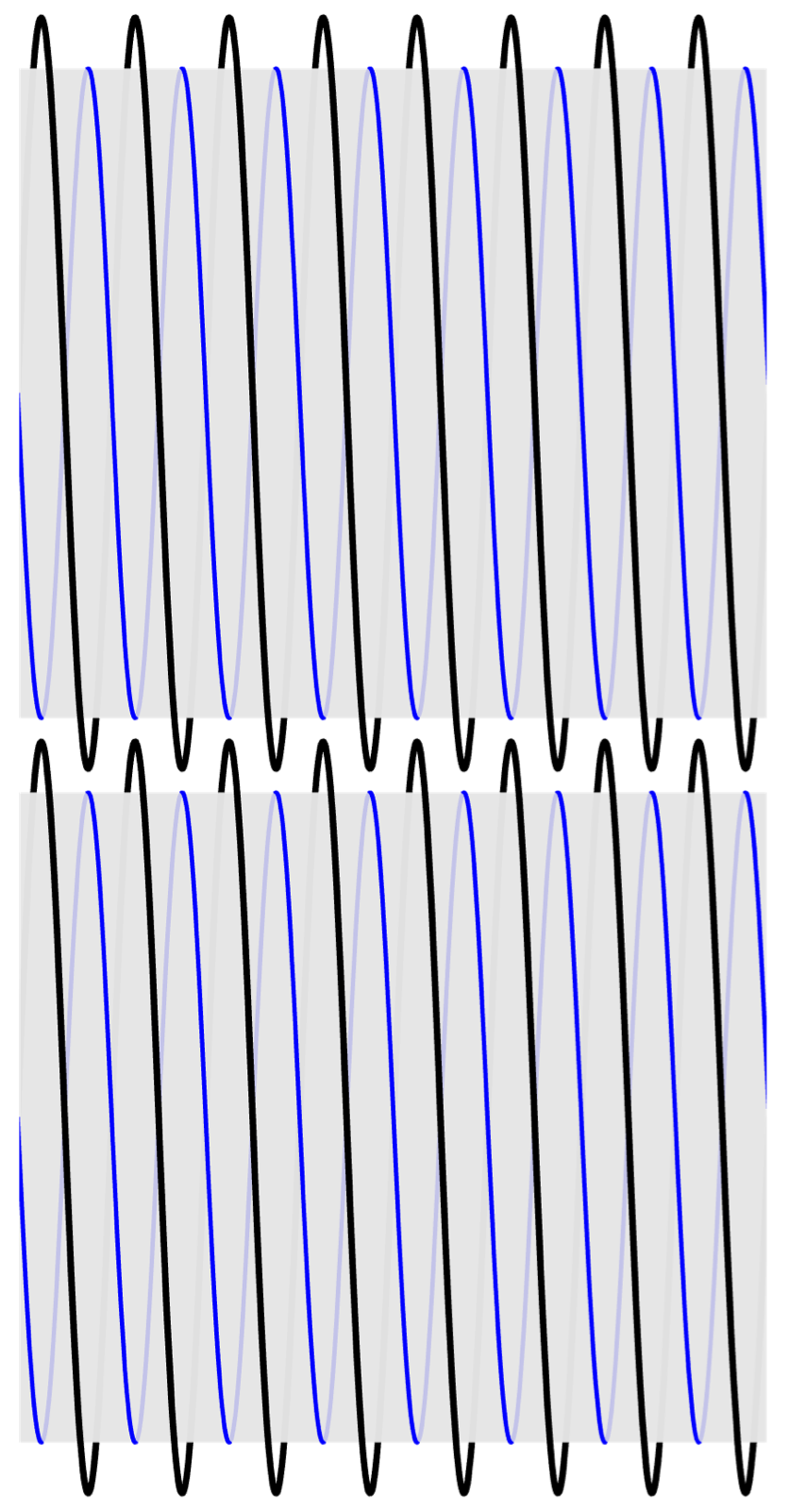
顺便说一句,我使用了特定螺栓的尺寸来制作图纸:1 英寸粗螺纹 (UNC) 螺栓。 大径为 1 英寸,小径为 0.8647 英寸,螺距为 0.125 英寸。 任何螺栓都可以,但我想要使用真正的螺栓。 我将在以后的文章中解释我是如何制作这些图纸的。
我们正在从侧面直接观察螺栓,采用的是正交投影,因此没有透视效果。 这将帮助我们了解螺栓在相互环绕时如何在轴向方向上移动(或不移动)。 这种视图清楚地表明,峰和谷彼此相对; 每个峰的对面都是一个谷。
在当前位置,顶部螺栓的底部与底部螺栓的顶部啮合。 峰嵌入谷中。 我们将标记顶部螺栓的一个峰和它嵌入的底部螺栓的谷。
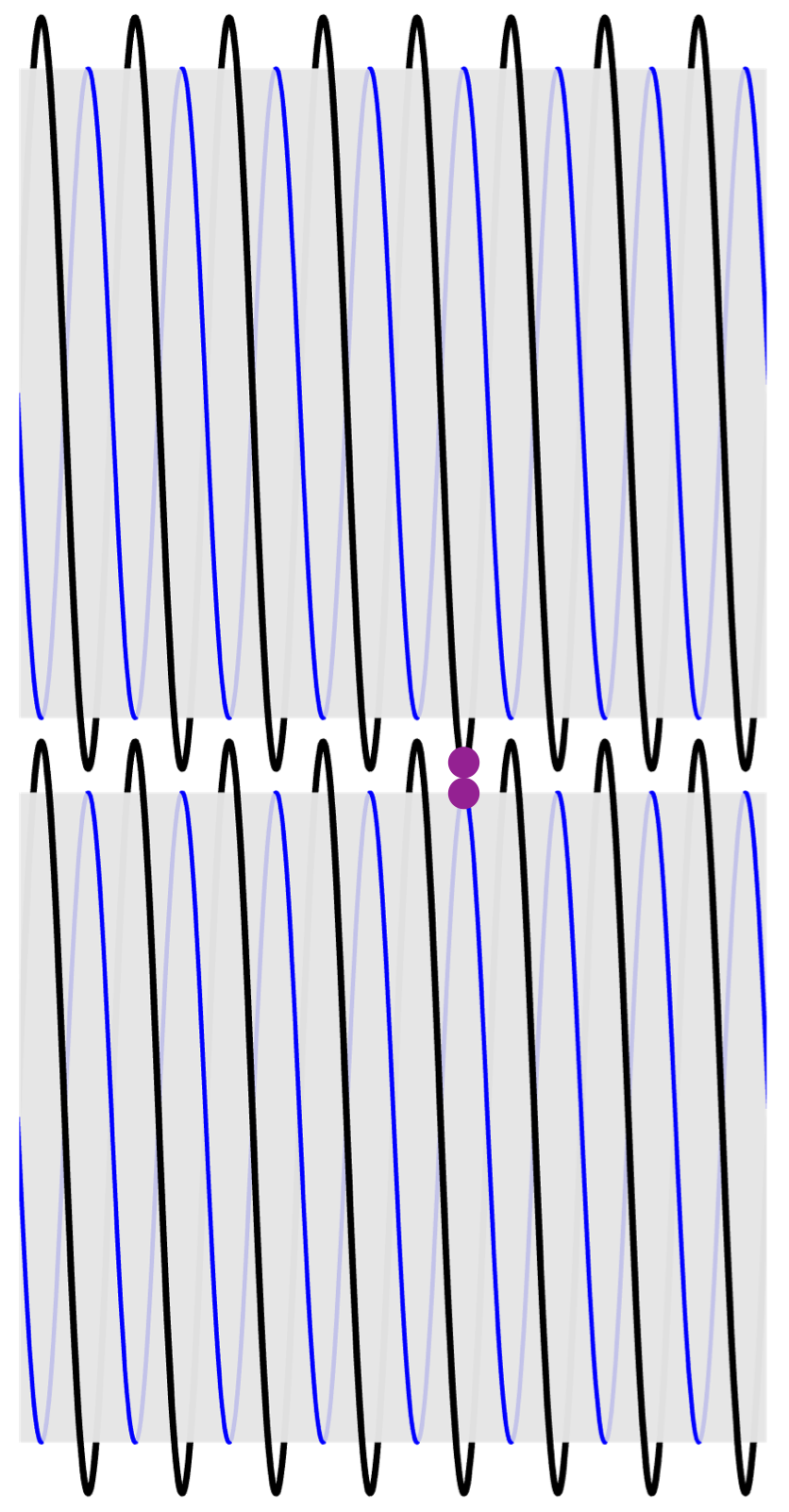
现在想象一下每个螺栓完成半个轨道运动,顶部螺栓摆动到后面,底部螺栓从前面上来。 因为螺栓都不会旋转,所以现在顶部螺栓的顶部最终将与现在底部螺栓的底部接触。 如果你沿着顶部螺栓的黑色(峰)线从紫色圆点沿着近侧向上到顶部,那就是在半个轨道运动期间将保持接触的部分。 同样,如果你沿着底部螺栓的蓝色(谷)线从紫色圆点沿着远侧(通过查看半透明的螺杆)向下到底部,那就是在半个轨道运动期间将保持接触的部分。
换句话说,下图中标出的两个点(仍然以原始配置绘制)是在半个轨道运动后将接触的点。
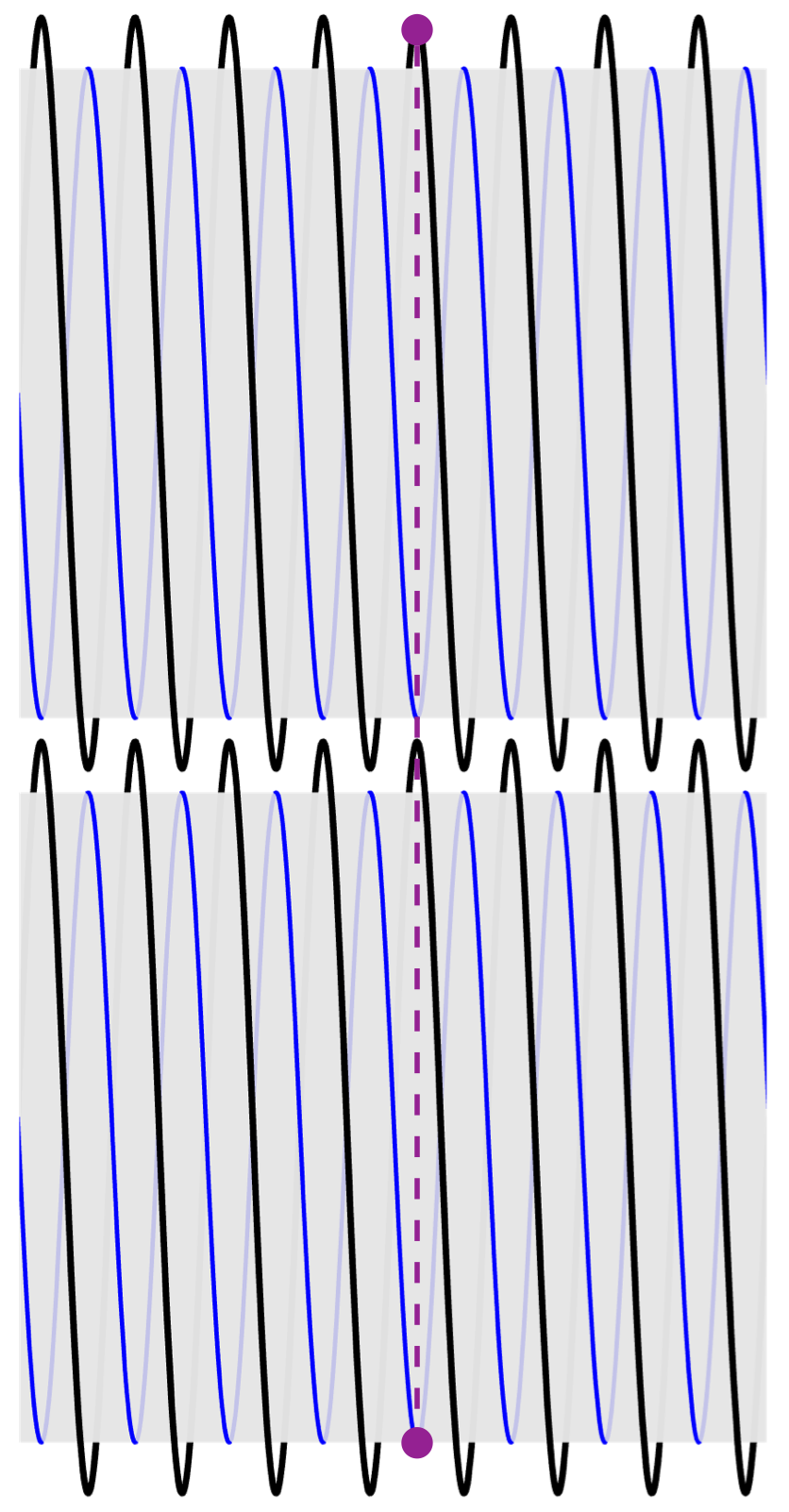
虚线垂直线显示这两个点在半个轨道运动之前是对齐的。 并且它们必须在半个轨道运动后对齐,因为它们处于接触状态。 由于它们在运动的开始和结束时都对齐,因此螺栓不会前进或后退 - 它们保持在相同的左右位置。 您可以使用四分之一轨道、完整轨道或轨道的任何倍数进行相同的论证。 由于两个螺栓上的螺纹几何形状相同,并且峰和谷彼此相对,因此螺栓在拨弄运动期间不会向左或向右移动。
Gardner 希望你解决这个问题,而无需抓住一对螺栓并尝试一下。 那样就算作弊了。 但是在解决难题之后,很高兴看到它在真正的螺栓上起作用。
Site search
Meta
- drdrang at leancrew
- Blog archive
- RSS feed
- JSON feed
- Mastodon
- GitHub repositories
Recent posts
- Bolts in Mathematica
- A SciAm bolt puzzle
- A Talk Show pair
- Apple’s weather direction
- Siri and license plates
- Chit chat about charts
- GIFs, transparency, and PIL
- Apple Ignorance
- A small note-taking change
- Rewriting a coin flipping script
- Loops and arrays
- Target practice and conditional probability
Credits
This work is licensed under a Creative Commons Attribution-Share Alike 3.0 Unported License. © 2005–2025, Dr. Drang