可微逻辑元胞自动机

从 Game of Life 到通过学习的循环电路进行模式生成

作者： Pietro Miotti Eyvind Niklasson Ettore Randazzo Alexander Mordvintsev

所属机构： Google, Paradigms of Intelligence Team

发布时间： 2025 年 3 月 3 日

想象一下，尝试逆向工程那些从简单规则中涌现出的复杂且常常出乎意料的模式和行为。几十年来，这一挑战一直激励着研究人员和元胞自动机爱好者。在元胞自动机中，我们通常采用自下而上的方法。我们选择局部规则，然后研究由此产生的涌现模式。如果我们能创建一些系统，给定一些复杂的期望模式，能够以完全可微的方式学习生成它的局部规则，同时保留元胞自动机固有的离散性质呢？这就是我们今天将与您一起探索的内容。

学习电路的放大视图 "G" 由学习电路生成

之前的工作探索了使用不可微技术学习转换规则，证明了为特定计算演化局部规则的可行性。同样，也存在先前对使一维元胞自动机可微的探索。我们提出了一种新颖的、完全端到端可微的方法，结合了人工智能领域的两个有趣的概念：Neural Cellular Automata (NCA) 和 Differentiable Logic Gates Networks。NCA 展现了学习任意模式和行为的能力，但它们并非固有地在离散状态空间中运行。这使得可解释性更具挑战性，并使它们陷入这样一种状态：当前硬件必须执行昂贵的矩阵乘法才能逐步更新其连续内部状态。同时，Differentiable Logic Gates Networks 已被用于发现组合逻辑电路，将离散状态与可微训练信号相结合。但它们尚未被证明可以在循环设置中工作。NCA 在空间和时间上都是循环的。听起来很吸引人，对吧？

放大来看，我们相信可微逻辑门和神经元胞自动机的集成是迈向可编程物质——Computronium——的潜在一步，这是一种理论上的物理物质，能够执行任意计算。Toffoli 和 Margolus 通过 CAM-8 开创了这个方向，这是一种基于元胞自动机的计算架构，理论上能够进行大规模的、水平可扩展的计算。然而，他们面临着一个根本性的挑战：实际制作实现所需宏观计算所需的局部规则，Amato 等人指出“其他研究人员 [...] 仍然担心找到与真实自然系统相对应的局部规则的难度”。如果我们能够直接学习这些局部规则，并创建将二进制逻辑、神经网络的灵活性和元胞自动机的局部处理相结合的模型呢？我们相信我们的原型可以让我们一窥计算的未来：可学习、局部和离散。

本文将引导您使用可微逻辑门实现元胞自动机，并在此过程中展示一些关键结果。

我们面临着两个根本问题。 ❓ Differentiable Logic CA 真的能学习吗？

为了回答这个问题，我们将首先攻击 Conway's Game of Life——也许是最具标志性的元胞自动机，几十年来一直吸引着研究人员。虽然第一个实验可能看起来过于简单（功能上等同于学习真值表），但它将证明我们设置的基本学习能力。更深刻的问题是： ❓ 空间和时间上的循环电路能否学习类似于传统 NCA 生成的复杂模式？

虽然 Differentiable Logic Gate Networks 和 Neural Cellular Automata (NCA) 都已证明具有可训练性，但在可微逻辑框架内，有效地训练表现出 NCA 的时间和空间循环的电路仍有待探索。

第二个实验将证明该模型学习循环电路的能力，这些电路生成类似于传统 NCA 生成的复杂模式。

回顾 - Neural Cellular Automata

该项目的核心是 Neural Cellular Automata (NCA)，它是经典元胞自动机与现代深度学习技术的结合。这种强大的范式，由 Mordvintsev 等人 开创，代表了我们思考可以生长、适应和自组织的计算系统方式的根本转变。

长期以来，传统元胞自动机以其通过简单局部规则生成复杂行为的能力吸引着研究人员。Neural Cellular Automata 通过使这些规则可以通过梯度下降学习，进一步扩展了这一概念。系统不是手工设计更新规则，而是自动发现它们，从而为自组织计算系统开辟了全新的可能性。

这种方法特别优雅的地方在于它保留了元胞自动机的核心原则——局部性、并行性和基于状态的计算——同时引入了神经网络的适应性。

在以下各节中，我们将总结“Growing Neural Cellular Automata”工作 的主要概念，该工作提出了一种为形态发生而开发的 Neural Cellular Automata。如果您已经熟悉它，请随时跳过它。

结构：智能单元的 2D 网格

系统的核心是一个 2D 网格，很像经典的元胞自动机。每个单元包含一个 n 维向量 的信息，该信息称为单元的 状态（或通道），对于 Growing-NCA 的特定情况，它由以下元素组成：

但神奇之处还不止于此。真正使该系统与众不同的是单元格如何通过两阶段过程进行交互和演变。

两阶段更新机制：感知和更新

  1. 感知阶段

在第一阶段，每个单元感知其环境。把它想象成一个单元格感知它周围的世界。为此，它使用 Sobel 滤波器，这是一种旨在以数值方式近似空间梯度（“其周围的变化”）的数学工具。滤波器按通道应用，结果称为 感知向量，它将单元格的当前状态与其收集的关于其环境的信息相结合。有点像生物细胞如何利用化学梯度来感知和响应其周围的环境。

  1. 更新阶段

接下来，神经网络介入。每个单元使用其感知向量作为神经网络的输入，神经网络对网格中的每个单元执行相同的操作。神经网络使用大约 8,000 个参数，根据它收集的信息确定每个单元应该如何变化。系统正是在这里演化的，单元格适应并响应环境变化。

Growing NCA 的学习过程，图片来自 Mordvintsev 等人。

可微性的力量

真正使该系统强大的是它的 可微性。从感知环境到更新其状态，每个操作都是完全可微的。这意味着我们可以通过 梯度下降 优化整个系统，就像神经网络从数据中学习一样。因此，系统并非静态地预定义了一些任意规则——它实际上可以 学习 生长特定的模式或行为，使其成为建模复杂系统的强大工具。

NCA Growing 过程，感谢

虽然系统的各个组件（如 Sobel 滤波器和神经网络）相对简单，但它们的组合创造了更复杂的东西。这是简单性和复杂性之间的平衡，就像自然界中的生物系统一样，局部相互作用导致了令人惊讶的、错综复杂的行为的出现。

这种方法不仅突破了元胞自动机可以做什么的界限，而且开辟了一个通过局部相互作用进行学习、生长和模式形成的世界。无论您是研究人员、开发人员，还是仅仅是对人工智能和复杂性交叉点感兴趣的人，这里都有很多值得探索的地方。

Neural Cellular Automata 的其他应用包括图像分割、图像分类等等。

回顾 - Differentiable Logic Gate Networks

如果我们能够采用计算的基本构建块（如 AND、OR 和 XOR 等逻辑门），并以学习的方式将它们组合起来，以解决某些任务呢？这正是 Deep Differentiable Logic Gate Networks (DLGNs) 所实现的，它将数字电路的效率与机器学习的力量相结合。这种由 Petersen 等人 开发的方法开辟了令人兴奋的可能性，尤其是在资源受限的环境中，如边缘计算和嵌入式系统。

卷积可微逻辑门网络，图片来自 Petersen 等人。

Deep Differentiable Logic Gate Networks 如何工作？

逻辑门作为神经元

DLGN 的核心是使用 逻辑门 作为其构建块，而不是神经网络中传统的神经元。在这种情况下，每个节点都是一个逻辑门，并且每个门执行简单的操作，例如 AND、OR、XOR 等，而不是执行加权和和矩阵乘法。

架构：

DLGN 的架构非常简单：

学习过程：使离散运算可微

该网络不学习权重，而是像传统的神经网络那样 学习每个门应执行哪个逻辑运算。在训练期间，每个节点都会解决一个分类任务，以识别要使用的正确逻辑门，从而最小化目标函数。

挑战在于逻辑门本质上是 离散 的且 不可微 的，这使得它们不适合基于梯度的学习。那么我们如何使它们学习呢？通过两个关键技巧：

  1. 连续逻辑运算

在训练期间，每个逻辑运算都由一个连续松弛代替，这是一个 可微版本，它对 0 和 1 之间的连续值进行运算。例如，我们不使用仅接受 0 或 1 的 硬 AND 门，而是使用 软 AND 门，它可以处理 0 和 1 之间的值作为输入，并传递两个输入的连续混合作为其输出。这些连续松弛（如下所示）允许我们使用 梯度下降 训练网络。

  1. 概率逻辑门选择

每个逻辑门维护一个关于两个输入的 16 种可能二进制运算的 概率分布。该分布由一个 16 维参数向量表示，然后使用 softmax 将其转换为概率分布。16 维向量的值在训练过程中被修改：随着时间的推移，逻辑门 学习 更喜欢一种运算而不是其他运算。

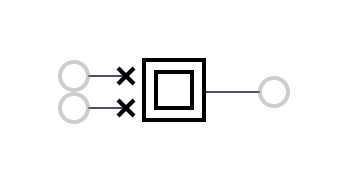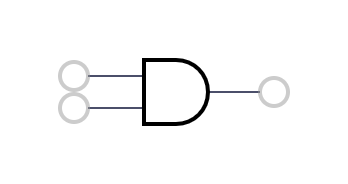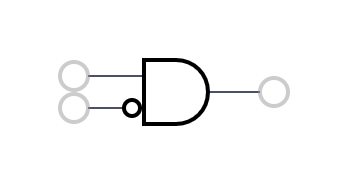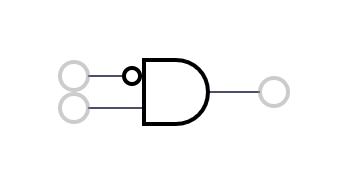Index | Operation | Continuous Relaxation | Symbol ---|---|---|--- 0 | FALSE | 0 | 1 | AND | a * b | 2 | A AND (NOT B) | a - a*b | 3 | A | a | 4 | (NOT A) AND B | b - a*b | 5 | B | b | 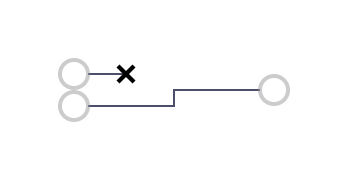6 | XOR | a + b - 2a ** b | 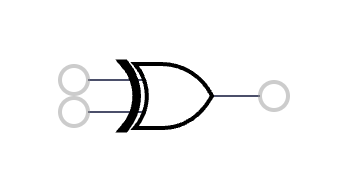7 | OR | a + b - a*b | 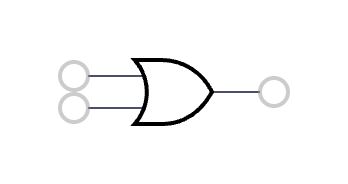8 | NOR | 1 - (a + b - a*b) | 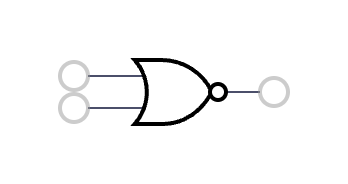9 | XNOR | 1 - (a + b - 2a*b) | 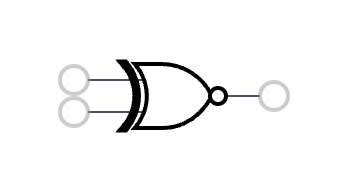10 | NOT B | 1 - b | 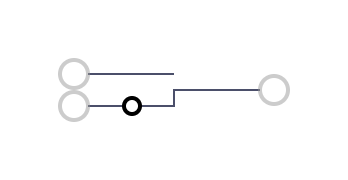11 | A OR (NOT B) | 1 - b + a*b | 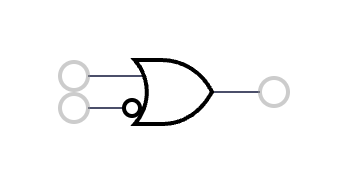12 | NOT A | 1 - a | 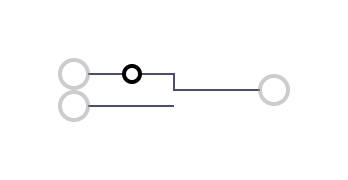13 | (NOT A) OR B | 1 - a + a*b | 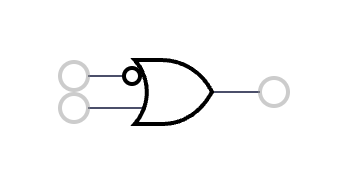14 | NAND | 1 - a*b | 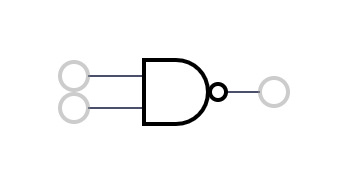15 | TRUE | 1 |

在 训练 期间，网络使用逻辑运算的连续松弛，但一旦网络被训练，我们就切换到 纯二进制运算 以实现闪电般的快速推理。

说明单个逻辑门训练的草图

为了方便训练的稳定性，逻辑门的初始分布偏向于 直通 门。

训练：学习逻辑门

训练过程遵循标准的正向-反向传递：

  1. 正向传递

    • 输入值通过网络传播。
    • 每个逻辑门在给定两个输入的情况下，使用其连续松弛计算所有 16 种可能的逻辑运算的结果。
    • 根据逻辑门的概率分布对这些结果进行加权，加权和 成为逻辑门的输出。

  2. 反向传递

    • 网络计算关于概率分布的 梯度，然后使用 梯度下降 更新这些分布。
    • 随着时间的推移，每个逻辑门的分布变得更加集中，并自发地收敛于一个运算，无论是 AND、OR、XOR 还是其他运算。

推理：二进制运算的魔力

训练完成后，我们可以冻结网络。这意味着每个逻辑门 都固定在其最可能的运算上，并且丢弃逻辑运算的连续版本。剩下的是一个 纯逻辑电路，它对二进制值（0 或 1）进行运算。

这种最终形式非常高效。当需要部署时，网络仅使用 二进制运算 运行，从而使其在任何硬件上都非常快。

Differentiable Logic Cellular Automata

将可微逻辑门网络与神经元胞自动机集成在一起，提供了一种处理离散状态同时保持可微性的解决方案。

让我们深入探索这个系统，检查它与传统 Neural Cellular Automata 的不同之处，同时突出它们的共同原则并理解可微逻辑门的基本作用。我们将借用 NCA 阶段的术语，突出显示我们的模型与传统 NCA 的不同之处。

结构：二进制智能单元的 2D 网格

与 NCA 一样，该系统构建在一个单元的 2D 网格上，其中每个单元的状态由 n 维二进制向量 表示。此二进制状态向量充当单元的工作内存，存储来自先前迭代的信息。在本文中，单元状态 和 通道 将互换使用。

两阶段更新机制：感知和更新

  1. 感知阶段

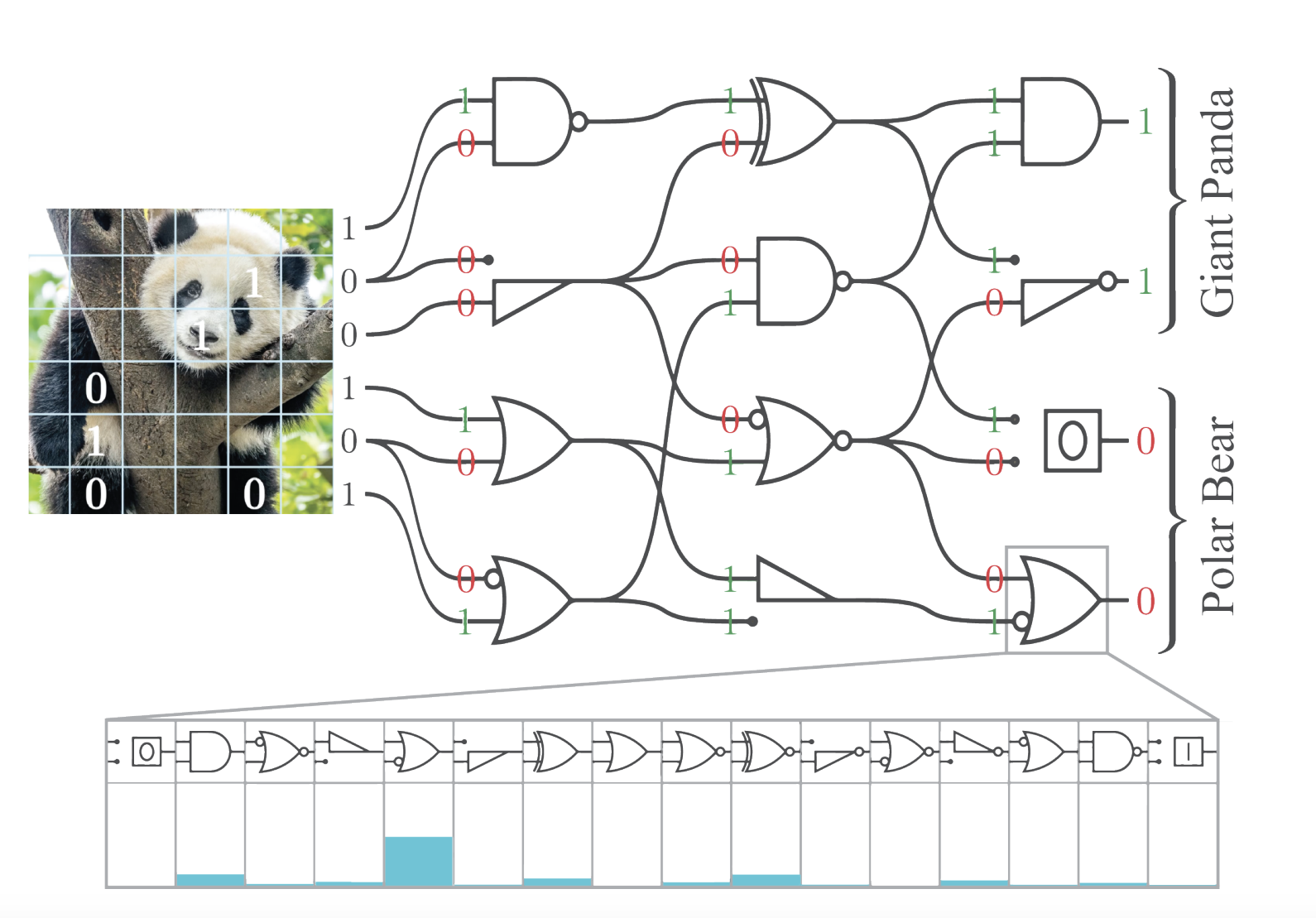
在元胞自动机系统中，每个单元必须了解其环境。虽然传统的 NCA 使用 Sobel 滤波器来模拟这种感知，但 DiffLogic CA 采用了一种不同的方法，遵循 。每个内核都是一个不同的电路，其中的连接是固定的并具有特定的结构，但是逻辑门是学习的。内核按通道计算。每个电路都采用四层，这些层的连接被设计为计算中心单元与其相邻单元之间的 交互，如图右所示。输出维度是内核数量乘以通道数量。其他方法包括每个通道具有多个输出位的内核，而不仅仅是一个位，这在某些情况下可以提高收敛速度。

每个内核按通道运行并计算中心单元与其相邻单元之间的交互，从而模拟 CA 在 Moore 邻域内的交互。此 3x3 块显示了 3 的状态维度。该电路连接到处理中心单元及其周围单元之间的交互。第一层有 8 个逻辑门，每个逻辑门都将中心单元作为其第一个输入，并将相邻单元作为其第二个输入。

  1. 更新阶段

更新机制遵循 NCA 范式，但采用 Differentiable Logic Network 来计算每个单元的新状态。网络的连接可以随机初始化，也可以专门构建以确保所有输入都包含在计算中。更新后的状态是通过将 Differentiable Logic Gate Network 应用于单元格先前内存（以灰色表示）的串联以及从其邻居接收到的信息（以橙色表示）来确定的。在标准的 NCA 中，此时，人们会逐步更新状态，将整个系统视为一个 ODE。对于 DiffLogic CA，我们直接输出新状态。

在给定维度为 4 和 2 个内核的单元状态的情况下，更新步骤的表示。

总之：感知阶段使用逻辑门网络来处理二进制邻域状态，取代了传统的基于卷积滤波器的操作，并且更新规则被实现为另一个逻辑门网络，该网络将感知输出和当前状态作为输入，并输出单元的下一个二进制状态。

4x4 DiffLogic CA 网格的示意图。在每个时间步，每个单元读取并处理存储在其相邻单元的状态中的信息，然后更新自己的状态

上图示意性地表示了一个 4x4 DiffLogic CA 网格，每个小方格都是一台具有双内存系统的微型计算机。我们将这两个寄存器分别可视化为灰色和橙色。我们网格中的每个单元都执行一个两步过程，我们稍后会看到该过程可以同步执行，或者在某些情况下异步执行：

  1. 第 1 步：感知阶段。首先，我们网格中的每个单元都成为数据收集器。他们检查邻居的灰色寄存器，处理他们观察到的内容，并将结果存储在他们的橙色寄存器中。

  2. 第 2 步：更新阶段。紧随其后，每个单元都成为决策者。该单元使用存储在其两个寄存器（原始灰色寄存器和新填充的橙色寄存器）中的信息，计算其新状态。这个新状态被写入灰色寄存器，而橙色寄存器被清除，为下一轮感知做好准备。

该系统的行为就像一个微型、独立的计算机网络，这些计算机与其邻居进行通信并根据他们的观察做出决策。每个单元都是一个巨大的、互连的网格中的微型处理器，通过这些简单的局部交互协同工作以执行复杂的计算。通过将局部连接与分布式处理相结合，我们构建了一些可以处理利用集体行为出现的任务的东西。

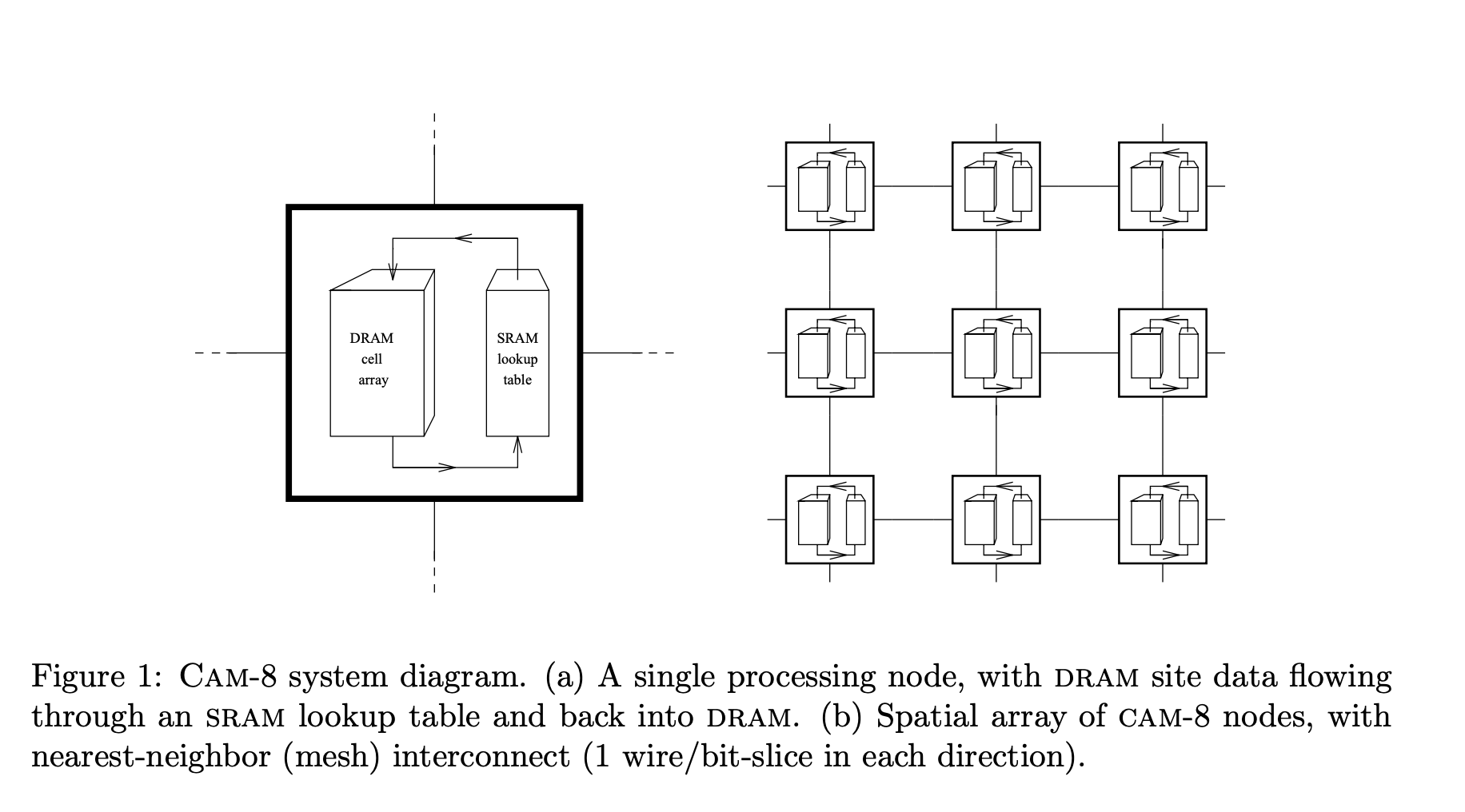
我们再次发现与 Toffoli 和 Margolus 的 Programmable Matter 和 Computronium 工作有着很强的亲缘关系，他们提出了 CAM-8，这是一种基于元胞自动机的计算机体系结构，与上述系统类似，其中每个单元使用 DRAM 芯片作为状态变量，并使用 SRAM 进行处理。

Cam-8 架构和图片来自 Margolus 等人。

实验 1：学习 Game of Life

Conway's Game of Life 是一个迷人的数学模拟，它展示了如何从简单的规则中涌现出复杂的模式。这个 游戏 由数学家 John Conway 于 1970 年创建，不是以传统意义上的方式进行的——它是一个元胞自动机，其中网格上的单元根据四个基本规则生存或死亡。尽管 Game of Life 非常简单，但它可以产生惊人的行为，从稳定的结构到似乎具有自己生命的动态模式。

Conway's Game of Life 模拟

游戏的规则非常简单，侧重于每个单元如何与其八个相邻单元交互：

  1. 出生：一个具有三个活着的邻居的死亡单元（当前值为 0）在下一代中焕发生机，就像通过繁殖一样。

  2. 生存：一个具有两个或三个活着的邻居的活着单元（当前值为 1）在下一代中存活下来，代表着一个平衡的环境。

  3. 人口不足：一个具有少于两个活着的邻居的活着单元在下一代中因孤立而死亡。

  4. 人口过剩：一个具有多于三个活着的邻居的活着单元在下一代中因拥挤而死亡。

这些规则同时应用于网格中的每个单元，从而创建了一种模式的舞蹈。从这些基本的相互作用中出现了复杂的行为：永不改变的 稳定结构、以有规律的模式脉动的 振荡器，甚至是在网格上移动的 滑翔机。正是这种从简单性中涌现出来的复杂性，使得 Game of Life 成为自然系统中自组织的有力隐喻，从生物进化到星系的形成。

鉴于其二进制和动态特性，Game of Life 是对 DiffLogic CA 进行健全性检查的好方法。

状态和参数

鉴于我们知道规则与之前的状态迭代无关，我们考虑一个由 1 位组成的单元状态，这意味着系统本质上是无记忆的。该模型架构包括 16 个感知电路内核，每个内核都具有相同的节点结构 [8, 4, 2, 1]。相反，更新网络有 23 层：前 16 层各有 128 个节点，随后的层分别有 [64, 32, 16, 8, 4, 2, 1] 个节点。

损失函数

损失函数通过对预测网格和真实网格之间的平方差求和来计算。 ∑i,jN(yi,j−y~i,j)2\sum_{i,j}^N(y_{i,j} - \tilde{y}_{i,j})^2 i,j∑N​(yi,j​−y~​i,j​)2

训练数据集

该模型在 3x3 周期性网格上训练一个时间步。鉴于 Game of Life 中的每个单元都与其八个邻居交互，并且其下一个状态由其当前状态及其邻居的状态决定，因此 3x3 网格存在 512 种可能的唯一配置。为了训练模型，我们构建了一个包含所有 512 种可能的网格配置的网格。正确学习网格的下一个状态意味着学习完整的 Game of Life 规则集。训练后的参数随后用于模拟模型在更大网格上的行为。

结果

在左侧，您可以观察到损失图，该图比较了逻辑门的两种表示形式。软 损失 使用它们的连续近似计算逻辑门的输出，如前一节所述，而 硬 损失 仅选择最可能的逻辑门并使用其离散输出。两种损失都完全收敛，表明我们能够生成一个完美模拟 Game of Life 的电路。

使用硬推理（选择最可能的逻辑门），右侧的模拟显示了学习电路在更大网格上的性能。出现的模式捕获了 Conway's Game of Life 中的结构：滑翔机在网格上移动，稳定块保持固定，以及像面包和船一样的经典结构保持其独特的形状。成功复制 Game of Life 的特征模式表明我们的电路已有效地学习了底层的局部规则。

DiffLogic CA 学习 Game of Life 的训练图

由学习电路模拟的 Game of Life

分析生成的电路

虽然电路优化不是本项目的主要重点，但本节提供了对生成电路的简要分析。

使用的 活动 逻辑门（不包括直通逻辑门 A 和 B）的总数为 336。通过检查逻辑门分布，我们观察到两个网络中最常用的逻辑门是 OR 和 AND。

所有感知内核电路中逻辑门计数的分布

更新电路中逻辑门计数的分布。

由于我们的最终电路只是一系列二进制逻辑门，我们可以更深入地了解并可视化所涉及的整个电路逻辑！下面是大多数这些 336 个逻辑门的可视化（当我们确定它们对输出没有贡献时，会修剪掉一些逻辑门）。

实现 Game of Life 的完整学习感知-更新电路（可交互访问）

左侧以三乘三网格排列的方块是输入逻辑门，它们按照从生命游戏中某个位置的单个中心单元的角度查看时的排列方式排列。当导线为高电平 (1) 时，其颜色为绿色，当为低电平 (0) 时，其颜色为红色。最后，每个逻辑门都应该是比较容易理解的，它们是 AND、OR 或 XOR 逻辑门之一，输入或输出上的小圆圈表示这些特定连接上的 NOT。此外，我们将二进制 NotB 和 NotA 逻辑门替换为一元 Not 逻辑门，并修剪掉未使用的输入，以简化可视化。最后，有些逻辑门只是“True”或“False”，并且它们看起来与输入几乎相同，表现为嵌套的方块，要么填充（True），要么为空（False）。

在最右侧，我们看到该电路的单个输出通道——表示 Game of Life 中单元的新状态。在图中的这种特定配置中，我们看到电路正确地计算了规则“任何具有三个活邻居的死亡单元都会变成活单元，就像通过繁殖一样。”

我们鼓励读者直接与电路交互。

实验 2：模式生成

Neural Cellular Automata (NCA) 在模式生成任务 中表现出了卓越的能力 ，这激励我们探索 diffLogic CA 的类似能力。在此任务中，系统从随机初始状态演化为目标图像，允许进行多个计算步骤。通过仅在最终时间步评估损失函数，我们挑战该模型发现离散转换规则，这些规则可以在没有逐步监督的情况下指导系统通过连贯的状态序列。

成功学习重建图像将验证两个关键方面：模型通过学习规则开发有意义的长期动态的能力，以及其有效学习 有状态的、时间循环的、空间循环的 电路的能力。这项研究尤为重要，因为它代表了据我们所知，对可微逻辑门网络在循环环境中进行的首次探索。

状态和参数

我们考虑 8 位的单元状态（通道），并迭代 DiffLogic CA 20 步。该模型架构包括 16 个感知电路内核，每个内核每层分别具有 8、4，然后是 2 个逻辑门。更新网络有 16 层：10 层各有 256 个逻辑门，然后是分别有 [128、64、32、16、8、8] 个逻辑门的层。

损失函数

我们将损失函数定义为在最后一个时间步，预测网格中第一个通道与目标网格之间的平方差之和。 ∑i,jN(yi,j,0−y~i,j,0)2\sum_{i,j}^N(y_{i,j,0} - \tilde{y}_{i,j,0})^2 i,j∑N​(yi,j,0​−y~​i,j,0​)2

训练数据集

该模型经过训练，可以在 20 个时间步内重建一个 16x16 的棋盘格图案。对于每个训练步骤，初始状态都是随机采样的。目标棋盘格图案显示在右侧。

目标图案

结果

DiffLogic CA 完全收敛于目标图案。训练图（左）显示软损失和硬损失函数一致收敛。用于计算损失函数的第一个通道（右）的演变显示了清晰的图案形成。一个有趣的涌现属性是从左下到右上的图案定向传播，尽管该模型没有内置的定向偏差。

DiffLogic CA 的训练图

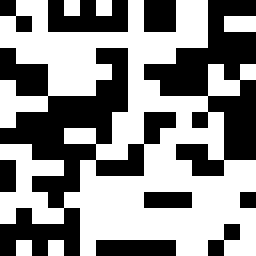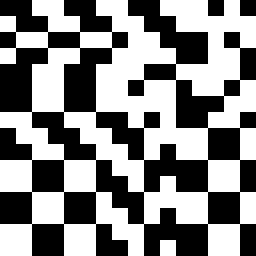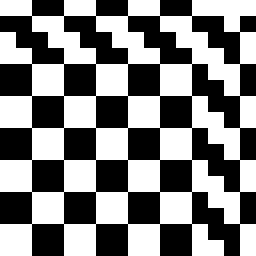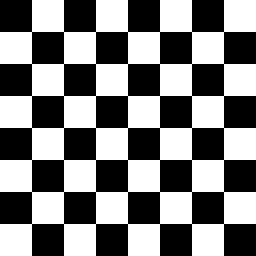diffLogic CA 的演变，仅考虑单元状态中的第一位。

分析生成的电路

使用的活动逻辑门总数（不包括直通逻辑门 A 和 B）为 22。对学习的逻辑门进行分析揭示了感知内核和更新网络之间不同的逻辑门分布。TRUE 逻辑门似乎在感知中起着关键作用，但在更新中没有。

所有感知内核电路中逻辑门计数的分布

更新电路中逻辑门计数的分布。

在下面，我们提供了修剪后的电路的交互式可视化。值得注意的是，我们只剩下六个逻辑门——其中一个是冗余的——相同输入之间的 AND。换句话说，电路学习的整个程序棋盘格生成函数可以使用仅五个逻辑门来实现。同样，大多数输入和输出仍然未使用。更值得注意的是，单元格自己的当前视觉输出甚至没有在更新步骤中被考虑。我们鼓励读者与下面的电路交互，单击并关闭左侧的输入以观察对输出的影响。

o: ch 7-i: ch 7, pos 6-o: ch 6-i: ch 4, pos 6-o: ch 5-i: ch 0, pos 0-o: ch 4-i: ch 6, pos 8-o: ch 3-o: ch 2-----i: ch 0, pos 6-o: ch 1-----i: ch 1, pos 8-i: ch 1, pos 0-o: ch 0--------i: ch 2, pos 6-----i: ch 3, pos 6-----i: ch 2, pos 8-i: ch 2, pos 0- 完整的学习感知-更新电路生成棋盘格，交互式

解决方案有多通用？

在肉眼看来，我们的解决方案似乎是迭代地构建网格——就像用砖头一块一块地砌成一样。但是，在训练期间，我们仅使用了一种固定尺寸的网格。自然地，我们应该研究如果我们更改网格尺寸会发生什么：我们学习的规则是否真的是一个迭代的、程序化的解决方案，或者它是否过度拟合到一种特定的网格尺寸？让我们将空间和