多连块平铺算法详解 (2018)
gfredericks.com | blog | 99 archive
多连块平铺算法详解
2018-08-18
更新:感谢 David MacIver 指出,这里的问题可以归结为 Exact Cover problem,并且 Donald Knuth 在他的 Dancing Links 论文中描述了这种归约方法。
八年多以前,我创建了 Polyomino Tiler (一个尝试用 polyominoes 集合平铺任意网格的浏览器应用程序),但我从未写过关于它所使用的算法。
如果以下内容有任何令人困惑的地方,可以先试用一下 polyomino tiler,以便更好地了解它的工作原理。
这个问题有几个方面结合在一起,使其具有挑战性:
- 可用的 polyomino 集合是完全可定制的,直到 heptominoes;每个 polyomino 可以被限制为特定的翻转/旋转。
- 网格可以是矩形网格的任何子集(或圆柱体/环面)。
因此,该算法需要足够通用,以免陷入由这两个事实导致的所有边界情况中。
该算法的两个关键组成部分是:
- 通过构建一个描述所有可能性的图来抽象几何细节。
- 对该图应用某些启发式方法到通用的回溯搜索算法中。
Placements (放置)
主要的预处理步骤是计算所有可用块的所有可能的放置。 当有数百个块变体可用时,此步骤可能需要很长时间,并且结果可能需要大量内存。 但结果本质上是一个二分图(或者,在数据库术语中,是 placements 和网格点之间的多对多关系)。
例如,给定这个 2x3 网格:
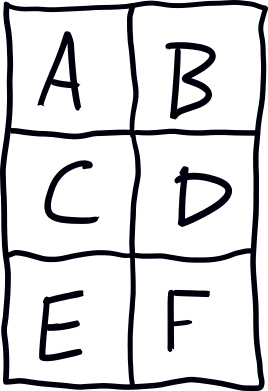
并将我们自己限制为 L 形 trominoes 以保持视觉上的易处理性,则放置图看起来像这样:

请注意,所有的几何细节都已被抽象出来。 这意味着该算法的其余部分也可以同样轻松地应用于三角形、六边形或双曲网格或更高维度的网格。
Search (搜索)
给定二分图,平铺网格的问题可以重新表述为找到 placements 的一个子集,该子集作为一个整体,恰好一次连接到每个网格点的问题。
搜索算法是一个 backtracking algorithm,它在每个步骤中选择一个未平铺的网格点以及与该网格点关联的随机 placement; 它将该 placement 添加到解决方案集中,然后尝试平铺网格的其余部分(注意哪些 placements 由于所选的 placement 而失效)。 如果无法平铺网格的其余部分,则尝试下一个 placement。 如果 placements 用完,则网格一定是不可平铺的。
例如,如果我们决定从网格点 A 开始平铺上面的网格,则搜索树可能看起来像这样:
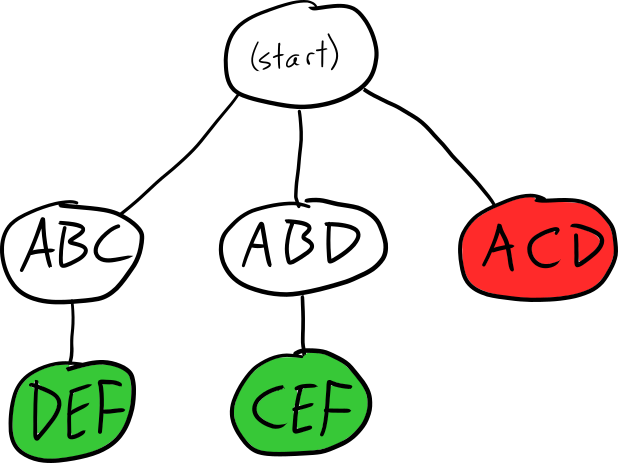
根据我们搜索子节点的顺序,我们最终可能会得到 ABC-DEF 平铺或 ABD-CEF 平铺; 如果我们首先访问 ACD 分支,我们将不得不回溯,因为该方向没有解决方案。
树如此稀疏的原因是,每次我们下降时,我们都会从图中删除与所选 placement 冲突的 placements。 例如,当我们下降到 ABC 时,图将更新为如下所示:
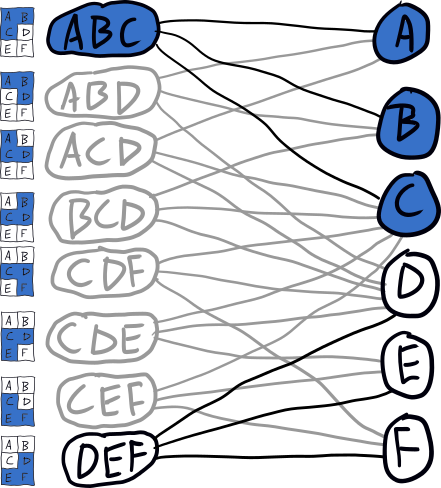
这种基本搜索算法通过几种启发式方法/优化进行了专门化。
Untileability from Zero Placements (零放置导致无法平铺)
由于我们选择的每个 placement 都会使其他几个 placements 变得不可能,因此很容易到达某个网格点不再有任何可能的 placements 的地步。 这是无法平铺的最常见迹象,这意味着我们需要回溯并尝试其他方法。
例如,如果我们沿着搜索树的 ACD 分支下降,该图将如下所示,并且存在没有 placements 的网格点表明没有解决方案。
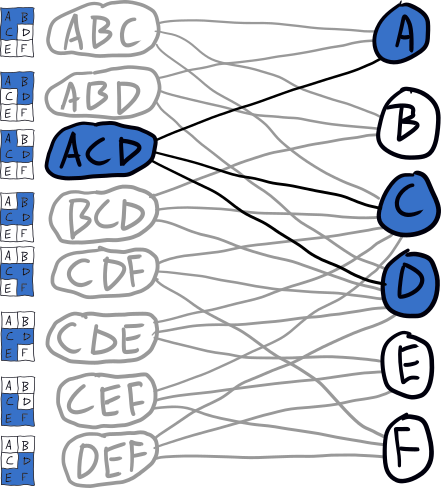
Untileability with Number Theory (数论判定无法平铺)
给定的一组 polyominoes 仅基于它们的大小对可以平铺的网格施加限制。 这完全是 polyominoes 的不同大小集合的函数。
例如,对于 tetrominoes,只能平铺大小是 4 的倍数的网格。 如果 polyominoes 的大小为 4 和 6,则只能平铺大小为大于 2 的偶数的网格。 这种分析与 coin problem 密切相关。
此外,如果一个网格由断开连接的子组件组成,那么我们可以分别分析每个子组件的可平铺性,并且如果任何子组件不可平铺,则可以得出整个网格不可平铺的结论。
例如,这个网格已被断开,即使这两个部分的大小加起来是 3 的倍数,因此理论上可以用 trominoes 平铺,但各个子组件_没有_ 3 的倍数的网格点,因此它们都不可平铺。

Smallest Subcomponents First (优先平铺最小子组件)
如果在任何时候网格变得断开连接,我们都会立即将算法限制为最小的子组件,并尝试在继续下一个子组件之前完全平铺它。 这里的逻辑是,如果整个断开连接的网格无法平铺,那么最小的子组件很可能也无法平铺。 最小的子组件也可能是我们可以最快完成搜索的子组件,因此这有望导致更积极地修剪搜索空间。
例如,此网格具有一个小组件和一个大组件,并且小组件无法用 trominoes 平铺(你能找出原因吗?); 首先平铺较小的子组件意味着我们可以快速发现此问题,而不是等到整个较大的子组件已被平铺。

Tile the most restricted grid points first (优先平铺限制最多的网格点)
在子组件中,我们根据剩余 placements 的数量选择要平铺的下一个网格点。 有时会存在只有一个选项的网格点,在这些情况下,立即放置该块非常重要,因为它可能会通过消除其他 placements(并可能导致更多网格点只有一个选项)来减小搜索空间的大小。
当没有具有单个 placement 的网格点时,我们仍然优先考虑具有最少数量 placements 的网格点,因为这些网格点在直觉上是网格中“最困难”的部分,这使得它们更有可能因其他 placements 而变得不可平铺。
例如,在此网格中,左下角未平铺的网格点只有一个可能的 trominoes placement; 平铺它让我们消除了另外七个与强制 placement 冲突的 placements。

Split the grid whenever possible (尽可能拆分网格)
最后一个启发式方法有点粗糙,但仍然有用。 动机是能够将网格拆分为子组件很有用(因为可以独立分析它们),因此如果我们有机会通过放置一个块来拆分它,我们应该这样做。 因此,精确的规则是,当没有单个 placement 网格点(这是更高优先级)时,并且存在一个网格点可以拆分网格(在图论术语中,一个顶点,其移除会断开该图的连接),那么我们将接下来搜索该网格点的 placements。
例如,有几个网格点可以将此网格的右下部分与其余部分断开连接; 可以选择其中任何一个作为下一个搜索步骤。

这种方法可以推广到某种倾向于选择使网格更容易拆分的网格点,而不仅仅是在一步就能实现此原理的情况下才采取行动。 但是,这可能会与最受限制的网格点的优先级排序有些紧张,因此我不确定它会如何运作。
Getting Stuck (卡住)
由于 polyomino 平铺问题是 NP-complete 的,因此该算法在各种情况下卡住并不奇怪。 其中一些是特定算法的伪影,可以想象对其进行调整以处理这些特殊情况。 但我认为目前的算法在广泛的功效和简单性之间取得了不错的平衡。
算法中的随机性(特定网格点的 placements 的排序,以及在有限的程度上网格点的优先级排序)意味着有时只需重新启动搜索就可以取得更多进展。
Possibilities (可能性)
可以对该算法进行各种调整; 我之前提到过一个关于更积极地拆分网格的想法。
另一个想法是优化尝试特定网格点的 placements 的顺序。 也许 placements 可以根据可用选项的数量来确定优先级。
Summary (总结)
因此,要用任意一组 polyominoes 平铺任意网格,我们:
- 计算所有可能的 placements 以获得网格点和 placements 之间的二分图
- 使用回溯算法搜索 placements 的子集,以精确平铺网格
- 通过使用各种启发式方法来优化算法以优先考虑其选择
事后看来,我认为将转换到图的初始步骤可以重新定向到转换到 SAT 问题的实例,在这种情况下,可以将通用的 SAT 求解器用于算法的其余部分。 了解我的算法中的哪些启发式方法在通用的 SAT 求解器中具有类似物,以及哪些是平铺问题特有的,将是一件有趣的事情。