日落几何学:用 Geometric Algebra 解决 (2016)
Shape Operator
作者: Jason Merrill jason@shapeoperator.com @shapeoperator
Sunset Geometry
2016年12月12日
Robert Vanderbei 撰写了一系列精彩的文章和报告,以及演讲,介绍了一种基于在平静的大湖上拍摄的日落照片来计算地球半径的方法。
Vanderbei 的分析是经典三角学中一个优雅而微妙的练习。 在这篇文章中,我想用不同的语言来展示另一种分析:Geometric Algebra。 我认为 Geometric Algebra 是一个比传统的“长度和角度”方法更强大的系统,它用于制定和解决三角学问题,并且应该被更多人了解。 Vanderbei 的日落问题简单易懂,但解决起来具有挑战性,因此它是一个不错的基准。
以下是 Vanderbei 的日落问题。 如果地球是平的,那么在水面上拍摄的日落照片看起来会像这样:
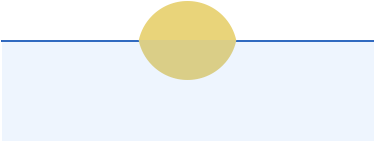
请注意,反射沉入地平线以下的部分与太阳在地平线上方突出的部分一样远。
在平静的水面上拍摄的实际日落照片(例如 Vanderbei 的照片⊕更新:我应该更加注意,大多数在水面上拍摄的日落照片实际上看起来不像 Vanderbei 的照片(或我的图表),因为波浪和大气效应,以及传感器饱和伪像使此类图像难以解释。 重现 Vanderbei 的图像可能介于困难和不可能之间。 更多信息请参见下文。)看起来更像这样:
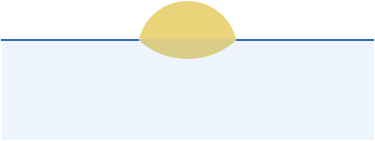
请注意缩短的反射。 发生这种情况是由于地球的曲率,通过测量这种效应的大小,可以推断出地球半径与相机在水面上方的高度之比⊕Vanderbei 方法的主要优点是证据是如此直接的视觉化(并且你可以在度假时用智能手机收集它)。 如果你想用类似的方法进行更简单、更好的测量,爬上山并使用星盘; 数学更简单,测量会更准确。。
Vanderbei 将太阳在地平线上方的角度称为 α\alphaα,并将太阳反射在地平线以下的角度称为 β\betaβ。 有了 Geometric Algebra,使用单位方向通常在代数上比角度更简单,因此我还会标记从相机到太阳顶部的单位方向 sss,到地平线的单位方向 ttt,以及水面上太阳反射底部的单位方向 www。
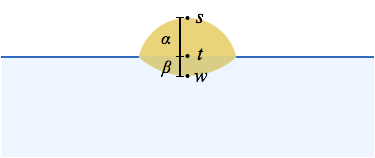
为了分析这个问题,考虑侧视图会很有帮助:
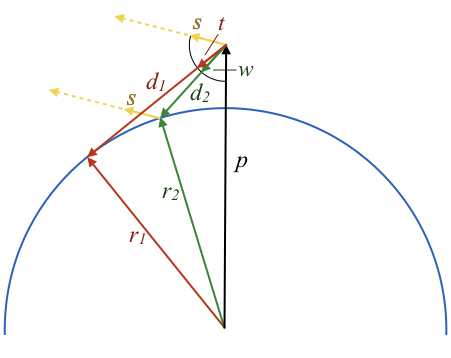
该图中有两个重要的三角形:由地球中心、相机和地平线形成的三角形(以红色绘制),以及由地球中心、相机和太阳从水面反射的反射点形成的三角形(以绿色绘制)。
三角形方程
三角形可以用向量表示,其代数表示非常简单⊕在这篇文章中,我遵循常见的 Geometric Algebra 惯例,将向量写成普通的、小写的字母,并使用希腊字母表示标量。 如果你习惯用粗体或 over-arrows 表示向量,这需要一些时间来适应,但跳过所有装饰可以更简单地处理大量向量。: r1−d1=pr2−d2=p \begin{aligned} r_1 - d_1 = p \\ r_2 - d_2 = p \end{aligned} r1−d1=pr2−d2=p
这些简单的向量和包含了所有关于长度和角度关系的信息,这些信息在经典三角学中通过“soh-cah-toa”、三角形假设(内角和为 180 度)、勾股定理以及余弦和正弦定律来表达。 这是一个很大的改进。
为了将其他向量与已知方向相关联,用先前定义的单位方向重新表达 d1d_1d1 和 d2d_2d2 会很有用: (1a) r1−∣d1∣t=pr_1 - |d_1|t = pr1−∣d1∣t=p (1b) r2−∣d2∣w=pr_2 - |d_2|w = pr2−∣d2∣w=p 换句话说,d1d_1d1 指向地平线,d2d_2d2 指向水面反射的底部。
除了这些三角形,还有一些显着的几何事实:
地平线条件
到地平线的视线与地平线处的地球相切,因此与通过地平线的地球半径垂直。 (2) r1⋅d1=r1⋅t=0r_1 \cdot d_1 = r_1 \cdot t = 0r1⋅d1=r1⋅t=0
反射条件
用角度表示,这表示为“入射角等于反射角”。 用向量表示,可以重述为 r2⋅s=−r2⋅wr_2 \cdot s = - r_2 \cdot wr2⋅s=−r2⋅w 或者 (3) r2⋅(s+w)=0r_2 \cdot (s + w) = 0r2⋅(s+w)=0
已知长度
我们知道其中一些向量的长度,以地球半径 ρ\rhoρ 和相机在海岸线上方的高度 δ\deltaδ 表示, (4a) r12=r22=ρ2r_1^2 = r_2^2 = \rho^2r12=r22=ρ2 (4b) p2=(ρ+δ)2p^2 = (\rho + \delta)^2p2=(ρ+δ)2 (4c) s2=w2=t2=1s^2 = w^2 = t^2 = 1s2=w2=t2=1 对第一个三角形方程 (1a) 的两边求平方,并使用地平线条件 (2)(或者等效地,使用勾股定理)也可以找到 d1d_1d1 的长度: (4d) d12=p2−r12=(ρ+δ)2−ρ2d_1^2 = p^2 - r_1^2 = (\rho + \delta)^2 - \rho^2d12=p2−r12=(ρ+δ)2−ρ2
方程 (1-4) 包含所有几何信息⊕通过在侧视图图上两次写入“s”,我假设了另一个重要的几何信息。 这对应于太阳与其他长度相比非常遥远(非常棒)的近似值。,需要根据给定的角度/方向(α\alphaα 和 β\betaβ,或 sss、www 和 ttt)和相机在海岸线上方的高度 δ\deltaδ,用代数方法求解地球半径 ρ\rhoρ。
介绍 Geometric Algebra
到目前为止,我已经用向量代数表达了一切,物理或工程专业的学生应该很熟悉(Gibbs 向量代数)。 为了实际求解方程,我将使用 Geometric Algebra 中的一些其他概念。
Geometric Algebra 是对“如果我可以乘以并除以向量会怎样?”这个问题的回答。 它在向量之间引入了一种新的结合律(但非交换律)可逆乘积:几何积。 向量 aaa 和 bbb 之间的几何积简称为 ababab。 向量与其自身的几何积等于标量(向量长度的平方), aa=a2=∣a∣2aa = a^2 = |a|^2aa=a2=∣a∣2 这一事实,再加上结合律和其他熟悉的乘法规则,足以唯一地定义几何积。
几何积的对称和反对称部分具有重要的几何意义,并且传统上被赋予它们自己的特殊符号⊕物理学家可能会感到困惑,他们意识到,基于 Geometric Algebra 的定义,平行向量是可交换的,而垂直向量是_反_交换的。 这还让你想起了什么?: (ab+ba)/2=a⋅b=b⋅a(ab−ba)/2=a∧b=−b∧a \begin{aligned} (ab + ba)/2 & = a \cdot b = b \cdot a \\ (ab - ba)/2 & = a \wedge b = - b \wedge a \end{aligned} (ab+ba)/2(ab−ba)/2=a⋅b=b⋅a=a∧b=−b∧a 我假设点积 a⋅ba \cdot ba⋅b 是熟悉的:它与一个向量在另一个向量上的投影有关,并且与它们之间角度的余弦成正比。
楔积 a∧ba \wedge ba∧b 可能只有在你研究过微分形式(当然还有 Geometric Algebra)时才熟悉,但它与更熟悉的叉积 a×ba \times ba×b 非常相似。 它表示由两个向量跨越的平行四边形的有向面积,并且与它们之间角度的正弦成正比⊕反对称性和双线性正是表示面积所需要的:一个向量与其自身不跨越任何面积(反对称性),并且平行四边形的面积与每个边的长度成线性比例(双线性)。楔积在线性代数中非常有用,因为它以一种可以用代数方式操作的方式表示由任意数量的向量跨越的线性子空间。叉积用垂直于该区域的向量表示有向面积(这种技巧仅在 3 维中有效),而楔积用另一种称为“双向量”的对象表示有向面积。楔积是结合律的(像几何积一样,但与叉积或点积不同),并且两个以上向量的楔积会构建更高“阶数”的对象。 3 个向量之间的楔积是表示有向体积(由它们跨越的平行六面体)的三向量,而 k 个不同向量之间的楔积是表示有向 k 维体积的 k 向量(在维度小于 k 的空间中始终为零)。
我们可以将这些定义颠倒过来,用点积和楔积来写几何积, ab=a⋅b+a∧b=⟨ab⟩0+⟨ab⟩2ab = a \cdot b + a \wedge b = \left\langle a b \right\rangle_0 + \left\langle a b \right\rangle_2ab=a⋅b+a∧b=⟨ab⟩0+⟨ab⟩2 其中 ⟨ab⟩0\left\langle a b \right\rangle_0⟨ab⟩0 和 ⟨ab⟩2\left\langle a b \right\rangle_2⟨ab⟩2 是“标量部分”和“双向量部分”的符号。
关于这个对象有一件奇怪的事情:它表示两种不同“类型的事物”之和,即标量和双向量。 但这不应该比复数表示“实数”和“虚数”之和更令人困扰(事实上,复数和两个向量的几何积之间存在非常密切的关系)。 随着经验的积累,人们会清楚地意识到,标量和双向量的和正是以结合律和可逆的方式表示两个向量的乘积所需要的。
当处理向量方程时,几何积给了我们两个新的超能力:
求解涉及向量积的方程。
给定两个不同向量积的方程 ab=cdab = cdab=cd 如果 bbb 是已知的,我们可以通过右乘 b−1b^{-1}b−1(即除以 bbb)来求解 aaa。 a=cdb−1a = cdb^{-1}a=cdb−1 b−1b^{-1}b−1 是明确定义的,要求 bb−1=1bb^{-1} = 1bb−1=1 左乘 bbb b2b−1=bb^2 b^{-1} = bb2b−1=b 并除以标量 b2b^2b2 b−1=bb2b^{-1} = \frac{b}{b^2}b−1=b2b 将此与点积和叉积/楔积进行对比。 一般来说,即使 bbb 是已知的,也不可能唯一地求解以下任何一个方程以获得 aaa。 a⋅b=c⋅da∧b=c∧da×b=c×d \begin{aligned} a \cdot b & = c \cdot d \\ a \wedge b & = c \wedge d \\ a \times b & = c \times d \end{aligned} a⋅ba∧ba×b=c⋅d=c∧d=c×d 第一个方程仅确定与 bbb 平行的 aaa 的部分,第二个方程仅确定与 bbb 垂直的 aaa 的部分。 你需要这两个才能求解所有 aaa,这就是单个几何积给你的。
向量之间的传递关系
经常发生的情况是,我们知道两个向量 aaa 和 bbb 与第三个向量 ccc 的关系,并且我们想使用此信息来确定 aaa 和 bbb 之间的关系。 在代数上,我们可以取未知的积 ababab 并在因子之间插入恒等式 cc−1=cc∣c∣2=1cc^{-1} = \frac{cc}{|c|^2} = 1cc−1=∣c∣2cc=1 并重新结合 ab=a(cc−1)b=(ac)(c−1b)=1∣c∣2(ac)(cb)ab = a \left(cc^{-1}\right) b = \left(a c\right) \left(c^{-1} b\right) = \frac{1}{|c|^2}(ac)(cb)ab=a(cc−1)b=(ac)(c−1b)=∣c∣21(ac)(cb) 从而用已知的积 acacac 和 cbcbcb 重新表达未知的积 ababab。
因为 cc−1=1cc^{-1} = 1cc−1=1,所以我们可以将它插入到向量的任何乘积中方便的任何位置。 这具有与将向量分解为平行于 c 和垂直于 c 的部分相同的实际效果。 这是在整个数学中以多种形式出现的非常普遍的技术的一个例子:插入一个恒等式以将乘积分解为更简单的片段。
我们将在下面两次使用这个技巧来解决日落问题的一个关键时刻。
重新制定地平线和反射条件
为了有效地利用 Geometric Algebra 的工具,将方程 (2) 和 (3)(地平线和反射条件)用几何积而不是点积来重新制定是有用的。
地平线条件
考虑几何积 r1t=r1⋅t+r1∧t=r1∧tr_1 t = r_1 \cdot t + r_1 \wedge t = r_1 \wedge tr1t=r1⋅t+r1∧t=r1∧t 其中第一个等式是一般向量恒等式 ab=a⋅b+a∧bab = a \cdot b + a \wedge bab=a⋅b+a∧b 的表达式,第二个等式来自 r1⋅t=0r_1 \cdot t = 0r1⋅t=0,我们先前形式的地平线条件 (2)。
在二维中,只有一个单位双向量,称为 III,由任何两个正交单位向量 e1e_1e1 和 e2e_2e2 跨越: e1∧e2=e1e2=Ie_1 \wedge e_2 = e_1 e_2 = Ie1∧e2=e1e2=I 因此 r1∧tr_1 \wedge tr1∧t 与 III 成正比,并且由于 r1r_1r1 和 ttt 是正交的,我们可以写 (2’) r1t=r1∧t=∣r1∣∣t∣I=∣r1∣I=ρIr_1 t = r_1 \wedge t = |r_1||t|I = |r_1|I = \rho Ir1t=r1∧t=∣r1∣∣t∣I=∣r1∣I=ρI
反射条件
我们先前版本的反射条件 (3) 也具有正交条件的形式: r2⋅(s+w)=0r_2 \cdot (s + w) = 0r2⋅(s+w)=0 因此,类似于我们重写地平线条件的方式,我们可以用几何积重写它⊕在 Geometric Algebra 中还有另一种写反射的方式,它更常见:r2s=−wr2r_2 s = - w r_2r2s=−wr2 或 s=−r2−1wr2=−r2wr2−1s = - r_2^{-1} w r_2 = - r_2 w r_2^{-1} s=−r2−1wr2=−r2wr2−1。另一种形式对于将反射_组合_成旋转,或将旋转_分解_成反射非常有用,但是当需要求解 r2r_2r2 时,我们在这里使用的涉及形成正交向量的形式会更方便。 r2(s+w)=∣r2∣∣s+w∣Ir_2 (s + w) = |r_2| |s + w| Ir2(s+w)=∣r2∣∣s+w∣I 稍后简化代数,基于此方程定义一个新的单位向量: g≡s+w∣s+w∣ g \equiv \frac{ s + w }{|s + w|} g≡∣s+w∣s+w g2=1g^2 = 1g2=1 因此,反射条件变为 (3’) r2g=∣r2∣∣g∣I=∣r2∣I=ρIr_2 g = |r_2| |g| I = |r_2| I = \rho Ir2g=∣r2∣∣g∣I=∣r2∣I=ρI
求解地球半径
现在我们已经用几何积而不是点积重写了我们的主要几何条件,我们准备好求解三角形方程了。
首先,消除 ppp 并将 (1a) 和 (1b) 的左侧设置为彼此相等⊕这个涉及四个向量之和的方程是一个“四边形方程”,与我们之前的三角形方程完全相同:它表示我们图中的红色向量和绿色向量形成一个四边形。: r1−∣d1∣t=r2−∣d2∣wr_1 - |d_1| t = r_2 - |d_2| wr1−∣d1∣t=r2−∣d2∣w 大小 ∣d2∣|d_2|∣d2∣ 是未知的,因此我们可以继续求解它,但是更有效的方法是简单地以以下方式消除它。 首先,将方程的两边从右边乘以 www: r1w−∣d1∣tw=r2w−∣d2∣w2r_1 w - |d_1| t w = r_2 w - |d_2| w^2r1w−∣d1∣tw=r2w−∣d2∣w2 现在我们可以使用“等级分离”来分别考虑该方程的标量和双向量部分。 由于 w2w^2w2 是标量,因此 ∣d2∣|d_2|∣d2∣ 依赖性从双向量部分中消失: ⟨r1w−∣d1∣tw⟩2=⟨r2w⟩2\left\langle r_1 w - |d_1| t w \right\rangle_2 = \left\langle r_2 w \right\rangle_2⟨r1w−∣d1∣tw⟩2=⟨r2w⟩2 重新排列以隔离 ∣d1∣|d_1|∣d1∣ 项 ∣d1∣⟨tw⟩2=⟨r1w−r2w⟩2|d_1| \left\langle t w \right\rangle_2 = \left\langle r_1 w - r_2 w \right\rangle_2∣d1∣⟨tw⟩2=⟨r1w−r2w⟩2 我们现在可以利用地平线和反射条件,通过插入因子 tt=1t t = 1tt=1 和 gg=1g g = 1gg=1 并重新结合,用已知乘积来重写未知乘积 r1w r_1 wr1w 和 r2wr_2 wr2w(这是上面介绍的第二个“超能力”): ∣d1∣⟨tw⟩2=⟨r1ttw−r2ggw⟩2|d_1|\left\langle t w \right\rangle_2 = \left\langle r_1 t t w - r_2 g g w \right\rangle_2∣d1∣⟨tw⟩2=⟨r1ttw−r2ggw⟩2 我们可以使用地平线 (2’) 和反射 (3’) 条件将 r1tr_1 tr1t 和 r2gr_2 gr2g 都简化为 ρI\rho IρI: ∣d1∣⟨tw⟩2=ρ⟨Itw−Igw⟩2|d_1| \left\langle t w \right\rangle_2 = \rho \left\langle I t w - I g w \right\rangle_2∣d1∣⟨tw⟩2=ρ⟨Itw−Igw⟩2 现在将向量的几何积扩展为点积和楔积给出 ∣d1∣t∧w=ρI(g⋅w−t⋅w)|d_1| t \wedge w = \rho I (g \cdot w - t \cdot w)∣d1∣t∧w=ρI(g⋅w−t⋅w) 我已经删除了像 ⟨t⋅w⟩2=0\left\langle t \cdot w\right\rangle_2 = 0⟨t⋅w⟩2=0 和 ⟨I(t∧w−g∧w)⟩2=0\left\langle I (t \wedge w - g \wedge w)\right\rangle_2 = 0⟨I(t∧w−g∧w)⟩2=0 这样的项,因为它们不包含等级为 2 的部分。
我们可以通过取两边的平方量级来利用已知的长度 ∣d1∣2|d_1|^2∣d1∣2,该长度导出为 (4d): ∣d1∣2∣t∧w∣2=ρ2(g⋅w−t⋅w)2∣d1∣2=ρ2[(g⋅w−t⋅w)2∣t∧w∣2] \begin{aligned} |d_1|^2 |t \wedge w|^2 & = \rho^2 \left(g \cdot w - t \cdot w\right)^2 \\ |d_1|^2 & = \rho^2 \left[ \frac{\left(g \cdot w - t \cdot w\right)^2}{|t \wedge w|^2}\right] \end{aligned} ∣d1∣2∣t∧w∣2∣d1∣2=ρ2(g⋅w−t⋅w)2=ρ2[∣t∧w∣2(g⋅w−t⋅w)2] 为了进一步简化代数,对于括号中的项,引入 ϵ2≡(g⋅w−t⋅w)2∣t∧w∣2\epsilon^2 \equiv \frac{(g \cdot w - t \cdot w)^2}{|t \wedge w|^2}ϵ2≡∣t∧w∣2(g⋅w−t⋅w)2 它完全用已知方向乘积来编写。 这给出 ∣d1∣2=ρ2ϵ2|d_1|^2 = \rho^2 \epsilon^2∣d1∣2=ρ2ϵ2 现在从 (4d) 代入 ∣d1∣2|d_1|^2∣d1∣2 得到 (ρ+δ)2−ρ2=ρ2ϵ2(\rho + \delta)^2 - \rho^2 = \rho^2 \epsilon^2(ρ+δ)2−ρ2=ρ2ϵ2 两边除以 ρ2\rho^2ρ2 得到 (1+δρ)2−1=ϵ2\left(1 + \frac{\delta}{\rho}\right)^2 - 1 = \epsilon^2(1+ρδ)2−1=ϵ2 最后,我们可以求解 ρ\rhoρ,地球的半径⊕我(和 Vanderbei)在这里选择了正平方根。 如果有的话,负平方根代表什么? (5) ρ=δ1+ϵ2−1\rho = \frac{\delta}{\sqrt{1 + \epsilon^2} - 1}ρ=1+ϵ2−1δ
我们可以使用以下关系通过角度来重写 ϵ2\epsilon^2ϵ2,从而恢复 Vanderbei 的最终答案: t⋅w=cos(β)t∧w=sin(β)Ig⋅w=cos(γ)=cos(α+β2) \begin{aligned} t \cdot w & = \cos(\beta) \\ t \wedge w & = \sin(\beta) I \\ g \cdot w & = \cos(\gamma) = \cos\left(\frac{\alpha + \beta}{2}\right) \end{aligned} t⋅wt∧wg⋅w=cos(β)=sin(β)I=cos(γ)=cos(2α+β) 所以 ϵ2=(cos(γ)−cos(β))2sin(β)2 \epsilon^2 = \frac{\left(\cos(\gamma) - \cos(\beta)\right)^2}{\sin(\beta)^2} ϵ2=sin(β)2(cos(γ)−cos(β))2
从这个和 (5) 中,只需进行一些三角恒等式练习即可恢复 Vanderbei 的演讲 中的幻灯片 28 中给出的形式,但是我会展示两个更好的形式。
首先,是一个小角度形式。
使用一般近似值 1+x2≈1+x2/2forx≪1sinθ≈θforθ≪1cosθ≈1−θ2/2forθ≪1 \begin{aligned} \sqrt{1+x^2} &\approx 1 + x^2/2 &\mathrm{for}\quad x \ll 1 \\ \sin{\theta} &\approx \theta &\mathrm{for}\quad \theta \ll 1 \\ \cos{\theta} &\approx 1 - \theta^2/2 &\mathrm{for}\quad \theta \ll 1 \\ \end{aligned} 1+x2sinθcosθ≈1+x2/2≈θ≈1−θ2/2forx≪1forθ≪1forθ≪1 我们可以将 (5) 简化为 (5’) ρ≈2ϵ2δ≈8β2(β2−γ2)2δ\rho \approx \frac{2}{\epsilon^2}\delta \approx \frac{8\beta^2}{\left(\beta^2 - \gamma^2\right)^2} \deltaρ≈ϵ22δ≈(β2−γ2)28β2δ Vanderbei 照片中的角度非常小,因此此近似值的精度优于百万分之一⊕它也比 Vanderbei 先前给出的其他小角度近似值更简单。。 由于角度和相机高度的不确定性约为 10%,因此此小角度近似值肯定足够了。
事实上,当使用四舍五入(浮点)算法进行计算时,小角度形式 (5’) 实际上比 Vanderbei 给出的精确形式更准确。 出现这种违反直觉的事实是因为精确形式遭受了“灾难性抵消”,这是由于减去以四舍五入误差计算的近似相等的值的结果。
我们可以通过将精确表达式 (5) 的分子和分母乘以 1+1+ϵ21 + \sqrt{1 + \epsilon^2}1+1+ϵ2 来消除一个此类抵消发生的位置,以得到 (5’’) ρ=1+ϵ2+1ϵ2δ\rho = \frac{ \sqrt{ 1 + \epsilon^2 } + 1 }{\epsilon^2}\deltaρ=ϵ21+ϵ2+1δ 我们还可以通过使用一般的三角恒等式将表达式 ϵ2\epsilon^2ϵ2 中余弦的差替换为正弦的差来消除另一个抵消源⊕这个恒等式与球面三角学中的经典 Haversine 公式 有关。 Evelyn Lamb 写了一篇精彩的博客文章,介绍了 被遗忘的三角函数 动物园中的这个和其他生物。 cos(θ)=1−2sin2(θ2)\cos(\theta) = 1-2\sin ^2\left(\frac{\theta}{2}\right)cos(θ)=1−2sin2(2θ) 所以: ϵ2=4(sin2(γ2)−sin2(β2))2sin(β)2\epsilon^2 = 4 \frac{\left(\sin^2\left(\frac{\gamma}{2}\right) - \sin^2\left(\frac{\beta}{2}\right)\right)^2}{\sin(\beta)^2}ϵ2=4sin(β)2(sin2(2γ)−sin2(2β))2 这很有帮助,因为我们现在要减去两个非常接近 0 的数字,而不是非常接近 1 的数字,并且中间四舍五入到固定位数的数字对于接近 0 的数字比对于接近 1 的数字丢弃的信息更少。
将此 ϵ2\epsilon^2ϵ2 表达式插入 ρ\rhoρ 的非抵消形式 (5’’) 现在允许计算 ρ\rhoρ 而不会产生不必要的四舍五入问题。
为了用测量的参数评估 ρ\rhoρ,请将以下值插入到 (5’) 或 (5’’) 中 α=69px⋅0.5∘/317px=0.001899radβ=29px⋅0.5∘/317px=0.0007983radγ=α+β2=0.001349radϵ2=5.482×10−7δ=7ftρ=2.55×107ft=4836mi \begin{aligned} \alpha &= 69\ \mathrm{px} \cdot 0.5^{\circ}/317\ \mathrm{px} &=& 0.001899\ \mathrm{rad}\\ \beta &= 29\ \mathrm{px} \cdot 0.5^{\circ}/317\ \mathrm{px} &=& 0.0007983\ \mathrm{rad}\\ \gamma &= \frac{\alpha + \beta}{2} &=& 0.001349\ \mathrm{rad}\\ \epsilon^2 &= 5.482 \times 10^{-7} \\ \delta &= 7\ \mathrm{ft} \\ \rho &= 2.55 \times 10^{7}\ \mathrm{ft} &=& 4836\ \mathrm{mi} \end{aligned} αβγϵ2δρ=69px⋅0.5∘/317px=29px⋅0.5∘/317px=2α+β=5.482×10−7=7ft=2.55×107ft====0.001899rad0.0007983rad0.001349rad4836mi 这比真值 3960 英里大 20% ⊕它也与 Vanderbei 给出的 答案(幻灯片 28)的第二位不同。 我认为这归因于上面讨论的“灾难性抵消”,再加上低精度计算。。 还不错。
与其他系统的比较
经典三角学
此时,你可能认为我相信上面的分析比进行经典三角学更简单,这太疯狂了。 我们在高中学习了三角学,而且并不难,对吧? 并且 Geometric Algebra 分析涉及一堆不熟悉的符号,跟踪非交换乘法以及“双向量”的新几何概念⊕另一方面,它确实给了你代数超能力。。
但是这个问题对经典三角学的分析是_困难的_。 比你在高中解决的三角学问题更难。 如果你不相信我,在不参考 Vanderbei 分析的情况下尝试解决它。 或者甚至只是跟着 [演讲](https://www.shapeoperator.c