使用 E-Graphs 优化 Python 特性
 About
About UsOur ServicesPortfolioHow We Work
Our TeamIndustriesWork With UsBlog
Contact Us
About
About UsOur ServicesPortfolioHow We Work
Our TeamIndustriesWork With UsBlog
Contact Us

 Stephen Diehl
2025年3月18日
Stephen Diehl
2025年3月18日
使用 E-Graphs 优化 Python 特性
MLIREquality Saturatione-graphs
使用 E-Graphs 和 MLIR 优化 Python 特性.wav
0:00 / 0:00
我们已经探索了逐步更复杂的数值计算优化技术。我们从基本的 MLIR 概念开始,然后是内存管理和线性代数,最后是神经网络实现。每一层都增加了表达和优化计算的新功能。现在我们准备为 Python 表达式构建我们的第一个玩具编译器。
在本节中,我们将探索如何使用 egglog 库对 Python 表达式执行项重写和优化,并将它们编译成 MLIR。
本节的完整源代码可在 GitHub 上找到。
Equality Saturation 和 E-Graphs
在我们深入研究实现之前,让我们回顾一下 equality saturation 和 e-graphs 的关键概念。
例如,如果我们有以下重写规则:
x * 2→x << 1x*y/x→y
如果我们尝试将其应用于表达式 (a * 2)/2,它会变成 (a << 1)/2。但是,我们应该消去分子和分母中的 2,得到 a,从而得到一个更简单的表达式。重写规则的顺序很重要,我们希望找到一种最佳的重写规则顺序,根据成本函数将表达式简化为某种形式。这被称为 阶段排序问题。
egg 库采用一种方法,即穷尽地将所有可能的重写规则应用于表达式,从而通过使用 e-graph 有效地解决阶段排序问题。这种方法允许探索所有可能的重写规则,然后提取表达式的最佳形式。
例如,在线性代数中,使用 NumPy 进行矩阵运算(如转置、乘法)非常昂贵,因为它们涉及访问矩阵的每个元素。但是,存在大量的恒等式可用于减少运算次数。
像 LLVM 这样的编译器,甚至 MLIR 的 linalg 方言,都不知道这些恒等式,因此不一定可以通过应用重写规则来抽象掉昂贵的运算。但是,在高层级(我们的核心语言)中,我们可以使用 e-graph 来生成更有效的张量操作,然后再将其降级到 MLIR。
例如,以下恒等式在线性代数中非常常见:
(AB)T=BTAT(A B)^T = B^T A^T(AB)T=BTAT (AT)T=A(A^T)^T = A(AT)T=A
或者在 Python 中:
np.transpose(A * B) = np.transpose(B) * np.transpose(A)
np.transpose(np.transpose(A)) == A
通过应用这些规则,我们可以在编译时优化 NumPy 表达式,从而显着提高性能。例如,在我们的示例中,我们已成功地将三个循环(包括一次乘法和两次转置)减少到只有两个循环,其中包括一次乘法和一次转置。这种优化不仅简化了计算,而且提高了效率。在 NumPy 的常见用法中,存在许多此类优化的机会,通常被称为唾手可得的果实。可以系统地应用这些优化来减少所需的操作次数,从而简化数值计算的执行。这在 LLVM 的自动向量化生效之前尤其有益,因为它使我们能够充分利用表达式的潜力并获得更快的执行时间。
e-graph(equality graph,等式图)是一种紧凑地表示许多等效表达式的数据结构。e-graph 不是为表达式维护单一的规范形式,而是维护等效表达式的类。这种方法允许更灵活和高效的项重写。
让我们看一个使用 egglog 库进行基本简化的具体示例。首先,我们必须定义我们的表达式模型。
from__future__import annotations
from egglog import*
classNum(Expr):
def__init__(self, value: i64Like) -> None: ...
@classmethod
defvar(cls, name: StringLike) -> Num: ...
def__add__(self, other: Num) -> Num: ...
def__mul__(self, other: Num) -> Num: ...
# Create an e-graph to store our expressions
egraph = EGraph()
# Define our expressions and give them names in the e-graph
expr1 = egraph.let("expr1", Num(2) * (Num.var("x") + Num(3))) # 2 * (x + 3)
expr2 = egraph.let("expr2", Num(6) + Num(2) * Num.var("x")) # 6 + 2x
# Define our rewrite rules using a decorated function
@egraph.register
def_num_rule(a: Num, b: Num, c: Num, i: i64, j: i64):
yield rewrite(a + b).to(b + a) # Commutativity of addition
yield rewrite(a * (b + c)).to((a * b) + (a * c)) # Distributive property
yield rewrite(Num(i) + Num(j)).to(Num(i + j)) # Constant folding for addition
yield rewrite(Num(i) * Num(j)).to(Num(i * j)) # Constant folding for multiplication
# Apply rules until no new equalities are found
egraph.saturate()
# Check if expr1 and expr2 are equivalent
egraph.check(eq(expr1).to(expr2))
# Extract the simplified form of expr1
egraph.extract(expr1)
使用 egraph.display() 函数,我们可以可视化 e-graph。
等式饱和之前的输入表达式:
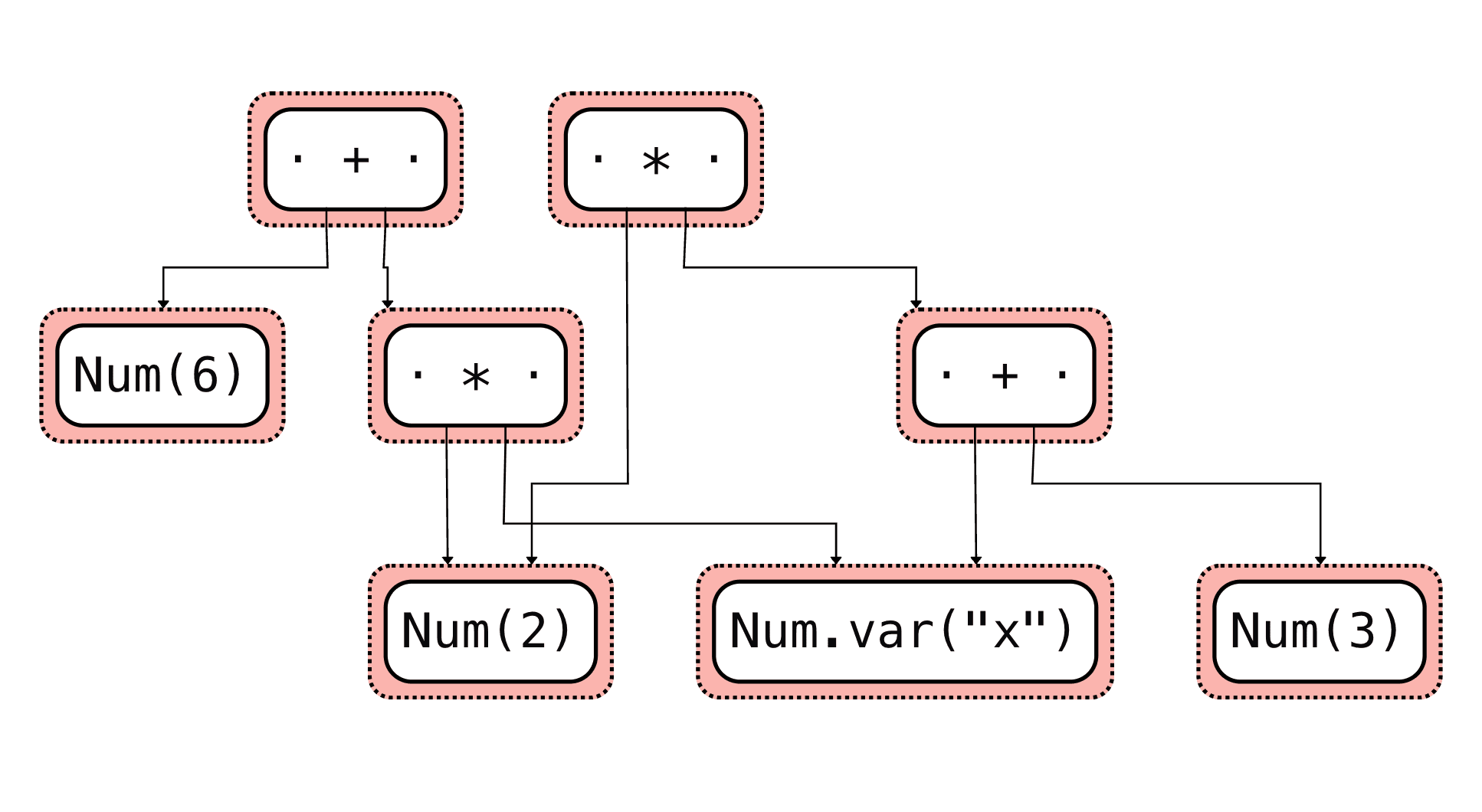
然后,具有所有等价类的输出是一个表达式网络:

从那里,我们可以根据自定义成本函数提取我们想要的表达式。
基础层
好的,现在让我们将其应用于我们的基本表达式编译器。我们的编译器管道有几个关键阶段:
- Python 函数装饰和类型注释
- 表达式树提取
- 使用 e-graphs 进行项重写和优化
- MLIR 代码生成
- LLVM 编译和 JIT 执行
我们编译器的基础层为表示和操作数学表达式提供了核心抽象。这一层至关重要,因为它构成了所有更高级别优化和转换的基础。让我们详细探讨每个组件。
表达式模型 (expr_model.py)
我们编译器的核心是一个表达式模型,它将数学表达式表示为抽象语法树 (AST)。该模型使用 Python 的 dataclasses 实现,以实现清晰高效的表示。
核心表达式类型
所有表达式的基类是 Expr 类,它提供了基本操作:
@dataclass(frozen=True)
classExpr:
def__add__(self, other: Expr) -> Expr:
return Add(self, as_expr(other))
def__mul__(self, other: Expr) -> Expr:
return Mul(self, as_expr(other))
# ... 其他操作
表达式模型由三种基本类型组成:
字面量(Literals):表达式中的常量
@dataclass(frozen=True)
classFloatLiteral(Expr):
fval: float# 浮点常量
@dataclass(frozen=True)
classIntLiteral(Expr):
ival: float# 整数常量
符号(Symbols):变量和函数名
@dataclass(frozen=True)
classSymbol(Expr):
name: str# 变量或函数名
运算(Operations):一元运算和二元运算
@dataclass(frozen=True)
classUnaryOp(Expr):
operand: Expr # 单个操作数
@dataclass(frozen=True)
classBinaryOp(Expr):
lhs: Expr # 左侧
rhs: Expr # 右侧
然后我们可以定义操作的实例。
@dataclass(frozen=True)
classAdd(BinaryOp): pass# 加法
...
@dataclass(frozen=True)
classSin(UnaryOp): pass# 正弦
内置函数 (builtin_functions.py)
内置函数模块为数学运算提供了类似 NumPy 的接口。这使得用户可以更轻松地使用熟悉的语法编写表达式,同时仍然可以利用我们的优化框架。它包括常见的数学常量和辅助函数,用于诸如绝对值之类的运算。
# 一个模拟的 NumPy 命名空间,我们将其转换为我们自己的表达式模型
import math
from mlir_egglog.expr_model import (
sin,
cos,
tan,
asin,
acos,
atan,
tanh,
sinh,
cosh,
sqrt,
exp,
log,
log10,
log2,
float32,
int64,
maximum,
) # noq
# 常量
e = math.e
pi = math.pi
# 定义 abs 函数
defabs(x):
return maximum(x, -x)
defrelu(x):
return maximum(x, 0.0)
defsigmoid(x):
return1.0/ (1.0+ exp(-x))
__all__= [
"sin",
"cos",
"tan",
"asin",
"acos",
"atan",
"tanh",
"sinh",
"cosh",
"sqrt",
"exp",
"log",
"log10",
"log2",
"float32",
"int64",
"e",
"pi",
"maximum",
"abs",
]
项 IR (term_ir.py)
Term IR 层提供了一种中间表示,针对项重写和 equality saturation 进行了优化。Term IR 的一个关键特性是不同操作的成本模型:
COST_BASIC_ARITH=1# 基本算术(单条 CPU 指令)
COST_CAST=2# 类型转换操作
COST_DIV=5# 除法
COST_POW_INTEGER=10# 整数幂
COST_SQRT=20# 平方根
COST_LOG=30# 对数
COST_EXP=40# 指数
COST_POW=50# 一般幂运算
COST_TRIG_BASIC=75# 基本三角函数
COST_HYPERBOLIC=180# 双曲函数
这些成本由 e-graph 优化引擎使用,以决定应用哪些转换。这些成本大致对应于现代硬件上每个操作的计算复杂度。
from__future__import annotations
import egglog
from egglog import StringLike, i64, f64, i64Like, f64Like # noqa: F401
from egglog import RewriteOrRule, rewrite
from typing import Generator
from mlir_egglog.expr_model import Expr, FloatLiteral, Symbol, IntLiteral
from abc import abstractmethod
defas_egraph(expr: Expr) -> Term:
"""
将语法树表达式转换为 egraph 项。
"""
from mlir_egglog import expr_model
match expr:
# 字面量和符号
case FloatLiteral(fval=val):
return Term.lit_f32(val)
case IntLiteral(ival=val):
return Term.lit_i64(int(val))
case Symbol(name=name):
return Term.var(name)
# 二元运算
case expr_model.Add(lhs=lhs, rhs=rhs):
# 其余操作
...
成本模型用于指导 e-graph 优化引擎,以根据我们的成本模型找到最具成本效益的实现。例如:
ex⋅ex⋅ex=e3xe^x \cdot e^x \cdot e^x = e^{3x}ex⋅ex⋅ex=e3x
LHS 有 3 个乘法,RHS 有 1 个乘法。因此应用于提取的成本将选择 RHS。
转换层
我们编译器最强大的功能之一是它能够以符号方式解释 Python 函数。此过程将常规 Python 函数转换为我们的 IR 表示,从而允许我们对生成的表达式树应用优化。
解释过程由 interpret 函数处理:
import types
import inspect
from mlir_egglog import expr_model as ir
definterpret(fn: types.FunctionType, globals: dict[str, object]):
"""
以符号方式解释一个 python 函数。
"""
# 获取函数的签名
sig = inspect.signature(fn)
# 为函数的每个参数创建符号参数
params = [n for n in sig.parameters]
symbolic_params = [ir.Symbol(name=n) for n in params]
# 将符号参数绑定到函数的参数
ba = sig.bind(*symbolic_params)
# 将我们的全局变量(即 np)注入到函数的全局变量中
custom_globals = fn.__globals__.copy()
custom_globals.update(globals)
# 创建一个具有我们自定义全局变量的临时函数
tfn = types.FunctionType(
fn.__code__,
custom_globals,
fn.__name__,
fn.__defaults__,
fn.__closure__,
)
return tfn(*ba.args, **ba.kwargs)
该函数首先进行参数分析,在其中分析输入函数的签名以确定其参数。对于每个参数,它使用我们的 Symbol 类创建一个符号表示。这些符号将用于跟踪表达式树中的变量。
接下来,将符号参数绑定到函数的参数槽,从而创建参数名称与其符号表示之间的映射。然后,该函数将我们的数学运算(如 NumPy 函数)的自定义实现注入到函数的全局命名空间中。这使我们能够拦截对这些函数的调用,并用我们的符号运算替换它们。
创建一个具有修改后的全局变量的临时函数,同时保留与原始函数相同的代码、名称和闭包。最后,使用符号参数执行该函数,从而生成表示计算的表达式树。
例如,给定一个 Python 函数:
deff(x, y):
return np.sin(x) + np.cos(y)
解释过程将:
- 为
x和y创建符号 - 将
np.sin和np.cos替换为我们的符号版本 - 使用符号输入执行函数
- 返回表示
Sin(Symbol("x")) + Cos(Symbol("y"))的表达式树
这种符号解释使我们能够以可以使用我们的 e-graph 机制优化的形式捕获 Python 计算。
IR 转换 (ir_to_mlir.py)
IR 到 MLIR 的转换层是我们高层表达式表示和 MLIR 的较低层方言之间的关键桥梁。此转换过程在 ir_to_mlir.py 中实现,涉及多个步骤,这些步骤利用 Python 的动态执行功能以及 AST 操作。
转换管道从 convert_term_to_expr 函数开始,该函数将 IR 项转换为我们的内部表达式模型。此函数采用 Python 的内置 ast 模块来解析和操作项的抽象语法树。此过程特别有趣,因为它使用 Python 的执行环境作为转换过程的一部分。
当接收到要转换的项时,它首先要经过 AST 解析。该函数从项的字符串表示形式创建一个 Python AST,这使我们可以在执行之前操作代码结构。此过程的关键部分是 mangle_assignment 函数,该函数确保表达式的结果正确地捕获在名为 _out 的变量中。此处理步骤至关重要,因为它提供了一种从执行环境中提取最终结果的方法。
执行环境是使用 function_map 字典精心构建的,该字典将运算名称映射到其相应的实现。此映射包括基本算术运算(Add、Sub、Mul、Div)、数学函数(Sin、Cos、Exp、Log)和类型转换运算(CastF32、CastI64)。这些运算中的每一个都映射到我们的表达式模型中的方法或我们的内置函数模块中的函数。
第二个主要组件是 convert_term_to_mlir 函数,该函数获取转换后的表达式并生成 MLIR 代码。此函数处理到 MLIR 文本格式的最终转换。它通过 argspec 参数处理函数参数,从而创建参数名称与其 MLIR 表示之间的映射(例如,将 x 转换为 %arg_x)。实际的 MLIR 生成委托给 MLIRGen 类,该类遍历表达式树并生成相应的 MLIR 运算。
例如,当转换像 a + b * c 这样的简单算术表达式时,管道将:
- 将表达式解析为 AST
- 使用函数映射将其转换为我们的内部表达式模型
- 生成具有适当内存引用和运算的 MLIR 代码
- 使用适当的类型注释将运算包装在适当的 MLIR 函数结构中
defconvert_term_to_expr(tree: IRTerm) -> ir.Expr:
"""
将项转换为表达式。
"""
# 将项解析为 AST
astree = ast.parse(str(tree))
# 处理赋值
astree.body[-1] = ast.fix_missing_locations(mangle_assignment(astree.body[-1])) # type: ignore
# 执行 AST
globals: dict[str, Any] = {}
exec(compile(astree, "<string>", "exec"), function_map, globals)
# 获取结果
result =globals["_out"]
return result
defconvert_term_to_mlir(tree: IRTerm, argspec: str) -> str:
"""
将项转换为 MLIR。
"""
expr = convert_term_to_expr(tree)
argnames =map(lambda x: x.strip(), argspec.split(","))
argmap = {k: f"%arg_{k}"for k in argnames}
source = MLIRGen(expr, argmap).generate()
return source
优化层
现在我们可以开始编写我们自己的重写规则,以应用于我们的表达式树。
birewrite_subsume 辅助函数是一个生成器,它为 e-graph 生成重写规则。它采用两个项并生成一个重写规则,该规则将第一个项转换为第二个项,从而使第一个项无法匹配或提取。我们使用它来单向地将通用 Terms 转换为专门的二元和一元运算。
defbirewrite_subsume(a: Term, b: Term) -> Generator[RewriteOrRule, None, None]:
yield rewrite(a, subsume=True).to(b)
yield rewrite(b).to(a)
基本简化模块实现了基本的数学重写,这些重写构成了我们的项重写系统的基础。这些规则组织在 basic_math 规则集中,包括以下几个关键类别的转换:
- 项转换规则(Term Translation Rules):这些规则允许在通用 Terms 与其专用形式(Add、Mul、Div、Pow)之间进行转换
- 恒等式规则(Identity Rules):用于处理像 x+0=xx + 0 = xx+0=x 和 x⋅1=xx \cdot 1 = xx⋅1=x 这样的数学恒等式的规则
- 结合律规则(Associativity Rules):处理像 (x+y)+z=x+(y+z)(x + y) + z = x + (y + z)(x+y)+z=x+(y+z) 这样的运算结合律的规则
- 幂规则(Power Rules):针对幂的特殊处理,包括像 x0=1x^0 = 1x0=1 和 x1=xx^1 = xx1=x 这样的情况
- 算术简化(Arithmetic Simplification):简化常见算术模式的规则,如 x+x=2⋅xx + x = 2 \cdot xx+x=2⋅x
每个规则都是使用 egglog 的重写系统实现的。
from mlir_egglog.term_ir import Term, Add, Mul, Div, Pow, PowConst, birewrite_subsume
from egglog import RewriteOrRule, ruleset, rewrite, i64, f64
from typing import Generator
@ruleset
defbasic_math(
x: Term, y: Term, z: Term, i: i64, f: f64
) -> Generator[RewriteOrRule, None, None]:
# 允许我们将 Term 转换为它们的专门化
yield from birewrite_subsume(x + y, Add(x, y))
yield from birewrite_subsume(x * y, Mul(x, y))
yield from birewrite_subsume(x / y, Div(x, y))
yield from birewrite_subsume(x**y, Pow(x, y))
# x + 0 = x (整数情况)
yield rewrite(Add(x, Term.lit_i64(0))).to(x)
# x + 0.0 = x (浮点情况)
yield rewrite(Add(x, Term.lit_f32(0.0))).to(x)
# 0.0 + x = x (浮点情况)
yield rewrite(Add(Term.lit_f32(0.0), x)).to(x)
# x * 1 = x
yield rewrite(Mul(x, Term.lit_i64(1))).to(x)
# x * 0 = 0
yield rewrite(Mul(x, Term.lit_i64(0))).to(Term.lit_i64(0))
# (x + y) + z = x + (y + z)
yield rewrite(Add(x, Add(y, z))).to(Add(Add(x, y), z))
# (x * y) * z = x * (y * z)
yield rewrite(Mul(x, Mul(y, z))).to(Mul(Mul(x, y), z))
# x + x = 2 * x
yield rewrite(Add(x, x)).to(Mul(Term.lit_i64(2), x))
# x * x = x^2
yield rewrite(Mul(x, x)).to(Pow(x, Term.lit_i64(2)))
# (x^y) * (x^z) = x^(y + z)
yield rewrite(Pow(x, y) * Pow(x, z)).to(Pow(x, Add(y, z)))
# x^i = x * x^(i - 1)
yield rewrite(Pow(x, Term.lit_i64(i))).to(PowConst(x, i))
# x^0 = 1
yield rewrite(PowConst(x, 0)).to(Term.lit_f32(1.0))
# x^1 = x
yield rewrite(PowConst(x, 1)).to(x)
# x^i = x * x^(i - 1)
yield rewrite(PowConst(x, i)).to(Mul(x, PowConst(x, i -1)), i >1)
与基本简化模块类似,三角简化模块提供了一套全面的规则,用于简化涉及三角函数和双曲函数的表达式。trig_simplify 规则集实现了几个重要的转换类别:
- 基本恒等式(Fundamental Identities):核心三角恒等式,如 sin2(x)+cos2(x)=1\sin^2(x) + \cos^2(x) = 1sin2(x)+cos2(x)=1
- 倍角公式(Double Angle Formulas):用于简化像 sin(x+y)\sin(x + y)sin(x+y) 和 cos(x+y)\cos(x + y)cos(x+y) 这样的表达式的规则
- 双曲恒等式(Hyperbolic Identities):类似的双曲函数规则,包括 sinh\sinhsinh、cosh\coshcosh 和 tanh\tanhtanh 的恒等式
这些规则对于优化涉及三角函数的数值计算尤为重要,这些函数在科学计算和机器学习应用程序中很常见。该模块仔细权衡了表达式简化和计算效率之间的折衷,使用 Term IR 中定义的成本模型来指导其决策。
from mlir_egglog.term_ir import Sin, Cos, Sinh, Cosh, Tanh, Term, Pow, Add
from egglog import ruleset, i64, f64
from egglog import rewrite
@ruleset
deftrig_simplify(x: Term, y: Term, z: Term, i: i64, fval: f64):
# 基本三角恒等式
# sin²(x) + cos²(x) = 1
two = Term.lit_i64(2)
yield rewrite(Add(Pow(Sin(x), two), Pow(Cos(x), two))).to(Term.lit_f32(1.0))
# 倍角公式
yield rewrite(Sin(x + y)).to(Sin(x) * Cos(y) + Cos(x) * Sin(y))
yield rewrite(Sin(x - y)).to(Sin(x) * Cos(y) - Cos(x) * Sin(y))
yield rewrite(Cos(x + y)).to(Cos(x) * Cos(y) - Sin(x) * Sin(y))
yield rewrite(Cos(x - y)).to(Cos(x) * Cos(y) + Sin(x) * Sin(y))
# 双曲恒等式
yield rewrite(Sinh(x) * Cosh(y) + Cosh(y) * Sinh(x)).to(Sinh(x + y))
yield rewrite(Cosh(x) * Cosh(y) + Sinh(x) * Sinh(y)).to(Cosh(x + y))
yield rewrite((Tanh(x) + Tanh(y)) / (Term.lit_i64(1) + Tanh(x) * Tanh(y))).to(
Tanh(x + y)
)
Egglog 优化器 (egglog_optimizer.py)
优化引擎将所有重写规则联系在一起,并为将优化应用于 Python 函数提供主要接口。它由几个关键组件组成:
- 规则组合(Rule Composition):顺序或并行组合多个规则集的能力
- 表达式提取(Expression Extraction):在 Python AST 和项表示之间进行转换的逻辑
- 优化管道(Optimization Pipeline):一种结构化的方法,用于应用规则直到达到固定点
- MLIR 生成(MLIR Generation):将优化的表达式最终转换为 MLIR 代码
优化器使用 e-graph 数据结构来有效地探索等效表达式,并根据我们的成本模型找到最具成本效益的实现。
import inspect
from types import FunctionType
from egglog import EGraph, RewriteOrRule, Ruleset
from egglog.egraph import UnstableCombinedRuleset
from mlir_egglog.term_ir import Term, as_egraph
from mlir_egglog.python_to_ir import interpret
from mlir_egglog import builtin_functions as ns
from mlir_egglog.expr_model import Expr
from mlir_egglog.ir_to_mlir import convert_term_to_mlir
# 重写规则
from mlir_egglog.basic_simplify import basic_math
from mlir_egglog.trig_simplify import trig_simplify
OPTS: tuple[Ruleset | RewriteOrRule, ...] = (basic_math, trig_simplify)
defextract(ast: Expr, rules: tuple[RewriteOrRule | Ruleset, ...], debug=False) -> Term:
root = as_egraph(ast)
egraph = EGraph()
egraph.let("root", root)
# 用户可以将规则组合为 (rule1 | rule2) 以并行应用它们
# 或 (rule1, rule2) 以顺序应用它们
for opt in rules:
ifisinstance(opt, Ruleset):
egraph.run(opt.saturate())
elifisinstance(opt, UnstableCombinedRuleset):
egraph.run(opt.saturate())
else:
# 对于单个规则,创建一个临时规则集
temp_ruleset = Ruleset("temp")
temp_ruleset.append(opt)
egraph.run(temp_ruleset.saturate())
extracted = egraph.extract(root)
# if debug:
# egraph.display()
return extracted
defcompile(
fn: FunctionType, rewrites: tuple[RewriteOrRule | Ruleset, ...] =OPTS, debug=True
) -> str:
# 根据命名空间映射转换 np 函数
exprtree = interpret(fn, {"np": ns})
extracted = extract(exprtree, rewrites, debug)
# 获取参数规范
argspec = inspect.signature(fn)
params =",".join(map(str, argspec.parameters))
return convert_term_to_mlir(extracted, params)
这些模块协同工作,提供了一个强大的系统来优化数学表达式,尤其是涉及三角函数和超越函数的表达式。该系统是可扩展的,允许轻松添加新规则,并为构建更专业的优化奠定了坚实的基础。
egglog 优化器支持两种组合重写规则的方式:并行组合和顺序组合。当使用 | 运算符组合规则(并行组合)时,它们在 e-graph 饱和过程的同一迭代中同时应用。这允许同时探索多个转换。相反,当使用元组或序列组合规则(顺序组合)时,它们会一个接一个地应用,每个规则集在移动到下一个规则集之前运行到饱和。当某些转换应仅在其他转换完成后尝试时,这种顺序方法可能很有用。
# 示例 1:并行组合
# 两个规则集在每次迭代中同时应用
parallel_rules = simplify_adds | simplify_muls
egraph = EGraph()
egraph.run(parallel_rules.saturate())
# 示例 2:顺序组合
# simplify_adds 在 simplify_muls 开始之前运行完成
sequential_rules = (simplify_adds, simplify_muls)
egraph = EGraph()
for ruleset in sequential_rules:
egraph.run(ruleset.saturate())
MLIR 生成 (mlir_gen.py)
MLIR 代码生成器负责将我们优化的表达式树转换为可执行的 MLIR 代码。生成器遵循一种系统的方法来生成可以有效处理 N 维数组的向量化内核。让我们检查一下关键组件和设计原则:
生成器生成一个遵循此模板的函数:
func.func @kernel_worker(
%arg0: memref<?xf32>,
%arg1: memref<?xf32>
) {
// 内核主体
}
生成的内核接受两个 memref 参数——一个输入缓冲区和一个输出缓冲区——并使用仿射循环逐元素地处理它们。这种设计允许对任何维度的数组进行有效的向量化运算。
func.func @kernel_worker(
%arg0: memref<?xf32>,
%arg1: memref<?xf32>
) attributes {llvm.emit_c_interface} {
%c0 = arith.constant 0 : index
// 获取输入数组的维度
%dim = memref.dim %arg0, %c0 : memref<?xf32>
// 以扁平化的方式处理每个元素
affine.for %idx = %c0 to %dim {
// 内核主体
}
return
}
表达式转换
MLIRGen 类实现了一种多通道转换策略,该策略从子表达式扩展开始,生成器使用 unfold 方法将表达式树展开为一组完整的子表达式。此过程确保识别公共子表达式并且可以重用。接下来,生成器采用拓扑排序,按复杂性对子表达式进行排序,使用字符串长度作为代理,以确保在可能依赖于它们的更复杂的表达式之前评估更简单的表达式。最后,执行代码生成管道,该管道首先从 memref 加载输入变量,为子表达式生成中间计算,并将最终结果存储回输出 memref。
生成器采用智能缓存机制来避免冗余计算:
defwalk(self, expr: ir.Expr):
if expr inself.cache:
return
deflookup(e):
returnself.cache.get(e) or as_source(e, self.vars, lookup)
self.cache[expr] = as_source(expr, self.vars, lookup)
这种缓存策略确保每个子表达式仅计算一次,通过 MLIR 的 SSA(静态单赋值)形式重用公共子表达式,并且生成的代码保持最佳效率。
MLIR 方言用法
然后,我们的生成器遍历表达式树并将我们的高层表达式映射到适当的 MLIR 方言:
- 算术运算使用
arith方言(例如,arith.addf、arith.mulf) - 数学函数使用
math方言(例如,math.sin、math.exp) - 内存运算使用
memref方言进行数组访问 - 循环结构使用
affine方言进行优化迭代
例如,像 sin(x) + cos(y) 这样的 Python 表达式将被转换为:
%a0 = math.sin %arg_x : f32
%a1 = math.cos %arg_y : f32
%a2 = arith.addf %a0, %a1 : f32
生成器自动处理类型转换,将浮点运算标准化为 f32,并根据需要将 i32 或 i64 用于整数运算。如果需要,会