从 Conway's Game of Life 半个世纪的发展历程中学习创新

从 Conway's Game of Life 半个世纪的发展历程中学习工程和创新？

Stephen Wolfram 2025年3月18日

元工程和创新法则

事物被发明，事物被发现。 不知何故，形成了一个进步的弧线。 但是，是否存在某种“创新法则”来管理进步的轨迹呢？

有一些指数和其他法则声称至少可以衡量进步的总体定量方面（芯片上的晶体管数量；一年内发表的论文数量等）。 但是，构成进步弧线的所有不同创新呢？ 我们是否有系统的方法来研究这些？

我们可以查看不同类型的自行车、火箭或微处理器的计划。 多年来，我们将看到连续创新的结果。 但是，大多数时候，这些创新不会停留在某个特定领域（例如自行车车架的形状）内。 相反，他们会不断地从其他领域汲取创新，例如新材料或新制造技术。 但是，如果我们想更接近对纯粹的创新现象的研究，我们需要一种情况，最好是在很长一段时间内，所有发生的事情都可以在一个狭义定义的框架内以统一的方式进行描述。

不久前，我意识到，实际上，是的，存在这样一种情况——而且我甚至亲自关注了大约半个世纪。 这是在 Game of Life cellular automaton 中构建“工程”结构的工作。 它们可以用作时钟、电线、逻辑门或生成 π 位数的东西。 但关键是它们都只是位的模式。 因此，当我们在这种情况下谈论创新时，我们谈论的是位的模式如何被发明或发现的相当纯粹的问题。

作为 cellular automata 科学的长期严肃研究者（以及它们通常所做的事情），我必须说，人们对 Game of Life 所做的事情的特殊性、异想天开和“非科学性”常常让我感到沮丧。 但我现在意识到的是，所有这些细节和所有这些努力现在创造了相当于工程创新的 独特数据集。 我的目标是做所谓的“元工程”——并研究自 Game of Life 发明以来近六十年来的工程过程中发生了什么。

我们将以相当纯粹的形式看到许多现象，这些现象至少在我们的整体进步和创新经验中是众所周知的。 大多数时候，第一步是确定一个目标：你可以描述并想要实现的目的。 （更罕见的情况是，人们观察到发生的事情，然后意识到有一种方法可以有意义地利用它。）但从一个目标开始，要么采取你拥有的组件，并投入人力来安排它们以“发明”可以实现目标的东西，或者实际上（通常至少在某种程度上是系统地和自动地）进行搜索以尝试“发现”实现目标的新方法。

当我们探索 Game of Life 所做的事情时，我们将看到偶尔的突然进步，以及更大的增量进步。 我们将看到正在构建的技术塔，并且我们将看到使用旧的、相当简单的技术来实现新目标。 但最重要的是，我们将看到通过搜索可能性发现的东西与通过明确的人力发明的东西之间的相互作用。

计算等价原理 意味着，从某种意义上说，像 Game of Life 这样的计算系统最终可以做的事情具有无限的丰富性——科学的作用是探索这种丰富性的广度。 但是，当涉及到工程和技术时，关键问题是我们选择让系统做什么——以及我们遵循哪些路径来实现它。 不可避免地，其中一些是由系统的底层计算结构决定的。 但很大程度上反映了我们人类做事的方式，以及我们所做的选择模式。 这就是我们将能够通过查看 Game of Life 上近六十年的工作来研究的东西——规模相当大。

这种“有目的的工程”的结果与生物学中发生的“盲目”适应性进化的结果有多相似？ 我 最近探索了适应性进化（碰巧，使用 cellular automata 作为模型），并看到它可以经常提供看似“新想法序列”的东西。 但是现在，在 Game of Life 的示例中，我们拥有可以明确识别为“新想法序列”的东西。 因此，我们能够将人工努力的结果（在许多情况下，在系统搜索的帮助下）与我们可以通过适应性进化的算法过程“自动”完成的事情进行比较。

最后，我们可以将原则上可以进行工程设计的事物的集合视为以某种“元工程空间”排列，正如我们可以将可以证明的数学定理视为 以元数学空间排列。 在数学案例中（尽管有 我自己的部分工作），历史上绝大多数定理都是纯粹通过人工努力发现的。 但是，正如我们将在下面看到的那样，在 Game of Life 工程中，这是人工努力和对元工程空间的相当自动化的探索的混合。 尽管如此，很像传统数学，我们在某种意义上仍然只追求我们已经概念化的目标。 通过这种方式，我们所做的事情与 我长期以来在研究科学方面所做的事情（或者，正如我现在所说的， ruliology）非常不同，即像 cellular automata（Game of Life 是一个例子）这样的计算系统“在野外”所做的事情，当它们不受我们试图用它们实现的目标的约束时。

Game of Life 的本质

这是一个 运行 Game of Life 的典型示例：

这里发生了很多复杂且难以理解的事情。 但仍然有一些可识别的结构，例如在连续步骤中交替出现的“blinkers" 和稳步穿过屏幕的“gliders”：

看到这些结构可能会让人认为应该能够在 Game of Life 中“进行工程设计”，设置最终可以做各种事情的模式。 事实上，我们这里的主要主题是自 Game of Life 推出以来近六十年来的此类工程的实际发展。

我们将重点关注 Game of Life 的本质“技术”：我们如何获取 Game of Life 提供的“原材料”，并从中制造出“有意义的工程结构”。

但是 Game of Life 的科学呢？ 我们能说什么 Game of Life “自然会做”，独立于我们在其中创建的“有用”结构？ 在过去半个世纪中，投入到 Game of Life 中的绝大多数精力都不是关于此的。 但这种基本问题是现在我 称之为 ruliology 中提出的问题—— 一种科学，我 一直在积极追求 自 20 世纪 80 年代初 以来。

一般来说，ruliology 着眼于系统类别，而不是 Game of Life 中通常探索的那种细节。 在 ruliology 中，Game of Life 在某种意义上没有什么特别之处； 它只是许多 “class 4” 2D cellular automaton 之一（在我的编号方案中，它是具有外部全代码 224 的 2 色 9 邻居 cellular automaton)。

我对 cellular automata 的研究特别关注 1D 而不是 2D 示例。 我认为这对于我所做的许多科学发现至关重要。 因为不知何故，通过能够一目了然地看到系统的历史，而不是仅仅看到视频中的帧掠过，人们会学到更多。 对于像 Game of Life 这样的 class 4 2D 规则，人们可以通过包含先前发生的“轨迹”来开始接近这一点，并且我们经常在下面使用 这种可视化： 我们可以通过查看 整个 (2+1) 维“时空历史” 来更完整地了解历史——尽管那时我们面临着 3D 形式，这些形式通常对于我们人类的视觉系统来说有些难以解析： 但是通过这个 3D 形式切片，我们获得了“轮廓”图片，结果看起来与我从 20 世纪 80 年代初开始跨越许多 1D cellular automata 大量生成的图片非常相似： 这些图片及其复杂的形式突出了即使在 Game of Life 中也很容易获得的 计算不可约性。 事实上，正是这种计算不可约性的存在最终使得可以在 Game of Life 中完成的工程的丰富性成为可能。 但在实际进行该工程中——以及在设置以可理解和“技术上有用”的方式运行的结构和流程中——我们需要保持计算不可约性“瓶颈”。 最后，我们可以将 Game of Life 中工程创新的路径视为一种在计算不可约性海洋中导航的努力，找到实现我们想要的“可约性岛屿”。

Game of Life 中制造了什么？

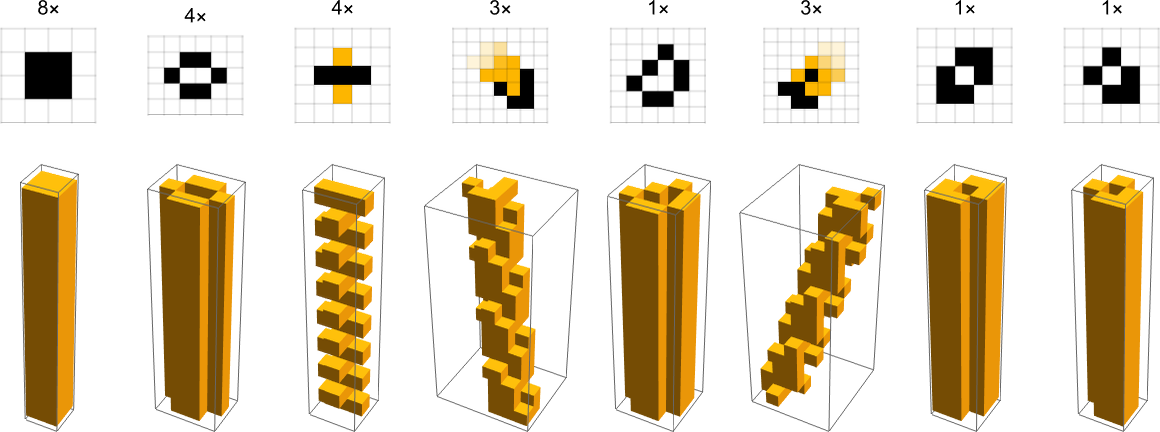
Game of Life 中大多数“具有工程意义”的结构在某种程度上是持久的。 最简单的是保持不变的结构，一些小的例子是： 是的，Game of Life 中的结构已被赋予各种（通常是异想天开的）名称，我将在此处使用它们。 （按照这种思路，Game of Life 中保持不变的结构通常被称为“still lifes”。）

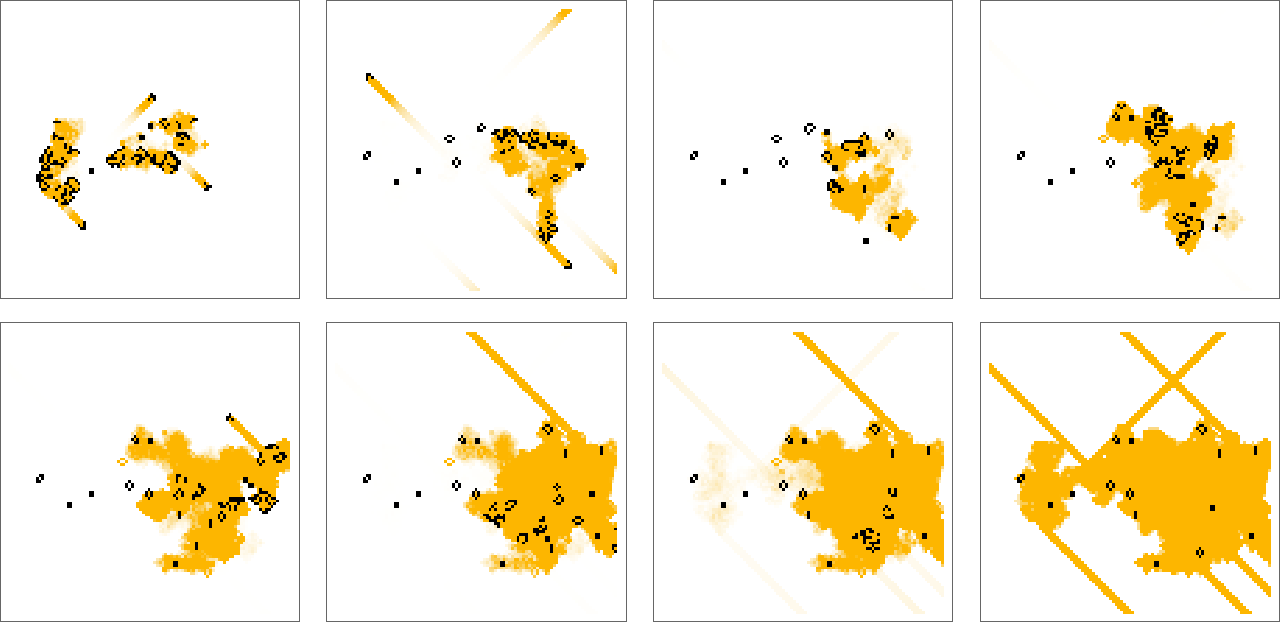
除了保持不变的结构外，还有产生周期性模式的“oscillators”： 我们将在下面更详细地讨论振荡器，但这里有一些示例（现在我们包括一个显示“轨迹”的可视化）： 在我们的结构类别库存中，下一个是“gliders”（或通常是“spaceships”）：每次循环时都会移动的结构。 一个典型的例子是 基本 glider，它每 4 步采用相同的形式——在水平移动 1 个单元格和垂直移动 1 个单元格后： 这里有一些这种“spaceship”风格结构的小例子： Still lifes、oscillators 和 spaceships 是在典型随机初始条件下幸存下来的“ash”中看到的大部分内容。 例如，我们在上一节中看到的演变的最终结果（在 1103 步之后）包括： 到目前为止，我们所看到的结构都是在 Game of Life 发明后不久发现的； 事实上，几乎在计算机上模拟后立即发现。 但它们都具有的一个共同特征是它们不会系统地增长； 它们总是返回到相同数量的黑色单元格。 因此，早期的惊喜之一（在 1970 年）是发现了一种每 30 步永远射出一个 glider 的“glider gun”： 给人一种 Game of Life“技术”进步的感觉的是，发现了一种 “更高效”的 glider gun（周期为 15），但仅在 2024 年，即前一个 glider gun 出现 54 年后： 在 Game of Life 的早期历史中迅速发现的另一种结构是“puffer”——一种“在身后留下碎片”的“spaceship”（在这种情况下，每 128 步）： 但有了这些“组件”，你能构建什么？ 早期构建的东西是“breeder”，它使用 glider 流来创建 glider gun，而 glider gun 本身随后会生成 glider 流： 原始模式覆盖约 25 万个单元格（其中 4060 个是黑色的）。 运行 1000 步后，我们看到它构建了一个包含数量呈二次方增长的 glider 的三角形： 好的，但是知道原则上可以“填充增长的空间区域”，是否有更有效的方法来做到这一点？ 正如 1993 年发现的那样，令人惊讶的简单答案是肯定的： 那么，在 Game of Life 中还能构建哪些其他类型的东西？ 很多，甚至从我们到目前为止所看到的简单结构中也可以构建。 例如，这是一个 构建用于计算质数的模式 仅当 n 是质数时，才在步骤 100 + 120 n 时发出一个“lightweight spaceship”。 当它在“时空中”查看时，它的工作原理就更明显了； 实际上，它 正在运行一个筛子，其中所有数字的所有倍数都被实例化为 glider 流，这些 glider 流会击落非质数位置生成的 spaceship： 如果我们查看这里的原始模式，它只是由相当简单的结构集合组成： 实际上，像这样的结构已被用于构建各种东西，包括例如 Turing machine emulators——以及 Game of Life 本身的 emulator，其中此 499×499 模式对应于单个模拟的 Life 单元： 这两个最后的模式都是在 20 世纪 90 年代构建的——由自 20 世纪 70 年代初以来就已知的组件构建。 正如我们所看到的——它们很大（而且很复杂）。 但它们需要这么大吗？ 计算等价原理的教训之一是，在计算宇宙中，几乎总有一种方法可以“做同样多的事情，但用更少的资源”。 事实上，在 Game of Life 中，过去几十年中已经沿着这些思路进行了许多许多发现。

正如我们将看到的，通常（但并非总是）这些发现建立在中间几年中确定的“新设备”和“新机制”之上。 这样一系列“设备”和“机制”涉及处理与 glider 流相关的“信号”。 例如，“glider pusher”（来自 1993 年）具有稍微微妙（但有用）的效果，即当 glider 经过时将其“推动”一个单元格： 另一个示例（实际上早在 1971 年就已知道，并且基于周期为 15 的“pentadecathlon”振荡器）是 glider 反射器： 但此 glider pusher 和 glider 反射器的一个特点是它们仅在 glider 和静态对象都处于相对于其周期的特定阶段时才有效。 这使得很难用这些构建更大的结构，这些结构可以正确运行（并且在许多情况下，如果不是由于原始 glider gun 的周期 30 和 glider 反射器的周期 15 的可公度性，那将是不可能的）。

glider 推动和 glider 反射能否更稳健地完成？ 答案是肯定的。 尽管直到 2020 年才创建了“bandersnatch”——一种完全静态的结构，可以独立于其阶段“推动” glider： 同时，在 2013 年创建了“snark”，它充当与阶段无关的 glider 反射器： 我们稍后将回到 的一个主题是，在 Game of Life 中首次构建某些功能之后，随之而来的是许多“优化”，从而以更稳健的方式、使用更小的模式等来实现该功能。 一种重要的方法围绕所谓的“hasslers”展开，它实际上允许人们通过提供“利用”来“挖掘”计算不可约性的小块，这些“利用”可以“控制”行为，通常在模式完成人们想要它们做的事情后将它们恢复到原始状态。

因此，例如，这是一个 hassler（碰巧就在 2025 年 2 月 8 日发现！），它将我们上面看到的第一个模式（在 1103 步中没有稳定）“利用”到一个周期为 80 的振荡器中： 并且基于此（事实上，当天晚些时候），使用它构建了 有史以来最紧凑的“spaceship gun”：

进步的弧线

我们讨论了多年来在 Game of Life 中可以构建的一些东西。 现在我想谈谈这是如何发生的，或者换句话说，Game of Life 中的“进步弧线”。 作为第一个迹象，我们可以绘制每年发现的新的 Life 结构的数量（或者，更具体地说，被认为足够重要以命名并在 LifeWiki 数据库 或其前身中记录的结构的數量）： 人们立即感受到几波活动。 我们可以将其分解为围绕各种常见结构类别的活动： 对于振荡器，我们看到五十年来的相当持续的活动，但最近加速增长。 对于“spaceship”和“gun”，我们看到从 20 世纪 70 年代初到 90 年代初的长期干旱期，此后活动相当稳定。 对于 conduits 和 reflectors，在 20 世纪 90 年代中期和 2010 年代中期分别达到突然的活动高峰之前，我们几乎看不到任何内容。

但是，实际上采取了哪些措施来找到所有这些结构？ 基本上有两种方法：构建和搜索。 构建是“显式工程”的故事，也是使用人类思想来构建人们想要的东西的故事。 另一方面，搜索是自动化的故事，也是采用算法生成的（通常是大型的）可能的模式集合，并对其进行测试以找到可以完成人们想要的事情的模式的故事。 尤其是在最近的时期，将这些方法交织在一起也变得很常见，例如使用构建来构建框架，然后使用搜索来查找实现该框架某些功能的特定模式。

当使用构建时，就像“发明”一个结构，而当使用搜索时，就像“发现”它。 那么，实际上正在做多少事情？ 对 最近记录的结构 的文本挖掘描述的结果如下——表明至少在最近，搜索（即“发现”）已成为寻找新结构的主要方法： 在 Game of Life 被发明时，人们很快就在计算机上运行它——并且人们试图对其可以做的事情进行分类。 Still lifes 和简单的振荡器立即出现。 然后——从我们在此处开头使用的 （“[R pentomino](https://writings.stephenwolfram.com/2025/03/what-can-we-learn-about