A (Long) Peek into Reinforcement Learning

日期：2018年2月19日 | 预计阅读时间：31分钟 | 作者：Lilian Weng

目录：

[更新于 2020-09-03：更新了 SARSA 和 Q-learning 的算法，使得差异更加明显。[更新于 2021-09-19：感谢 爱吃猫的鱼, 我们有了这个帖子的中文版.]

近年来，人工智能（AI）领域发生了一些令人兴奋的消息。AlphaGo 在围棋比赛中击败了最优秀的职业人类棋手。很快，扩展算法 [AlphaGo Zero](AlphaGo Zero) 在没有人类知识监督学习的情况下，以 100-0 击败了 AlphaGo。顶级的职业游戏玩家在 OpenAI 开发的 DOTA2 1v1 比赛中输给了机器人。了解这些之后，很难不好奇这些算法背后的魔力——Reinforcement Learning (RL)。我写这篇文章是为了简要地回顾这个领域。我们将首先介绍几个基本概念，然后深入研究解决 RL 问题的经典方法。希望这篇文章可以成为新手的良好起点，为未来的前沿研究搭建桥梁。

什么是 Reinforcement Learning?

假设我们有一个智能体在一个未知的环境中，这个智能体可以通过与环境互动获得一些奖励。智能体应该采取行动，以最大化累积奖励。在现实中，这种情况可能是一个机器人玩游戏以获得高分，或者一个机器人试图用物理物品完成物理任务；而不仅仅局限于这些。

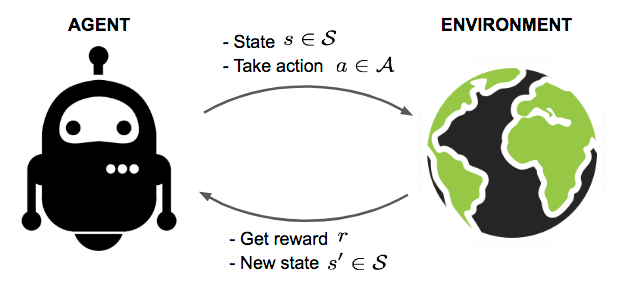图 1. 智能体与环境互动，试图采取明智的行动来最大化累积奖励。

Reinforcement Learning (RL) 的目标是从实验试验和收到的相对简单的反馈中为智能体学习一个好的策略。有了最佳策略，智能体就能够主动适应环境，从而最大化未来的奖励。

关键概念

现在让我们正式定义 RL 中的一组关键概念。

智能体在环境中行动。环境如何对某些行动做出反应由一个模型定义，我们可能知道也可能不知道这个模型。智能体可以停留在环境的许多状态 (s∈S) 之一，并选择采取许多行动 (a∈A) 之一，以从一种状态切换到另一种状态。智能体将到达哪种状态由状态之间的转移概率 (P) 决定。一旦采取行动，环境就会提供一个奖励 (r∈R) 作为反馈。

该模型定义了奖励函数和转移概率。我们可能知道也可能不知道模型是如何工作的，这区分了两种情况：

智能体的策略 π(s) 提供了在特定状态下采取什么最佳行动的指导方针，目标是最大化总奖励。每个状态都与一个价值函数 V(s) 相关联，该函数预测我们通过执行相应策略能够在当前状态获得的预期未来奖励金额。换句话说，价值函数量化了一个状态有多好。策略和价值函数都是我们在 Reinforcement Learning 中试图学习的东西。

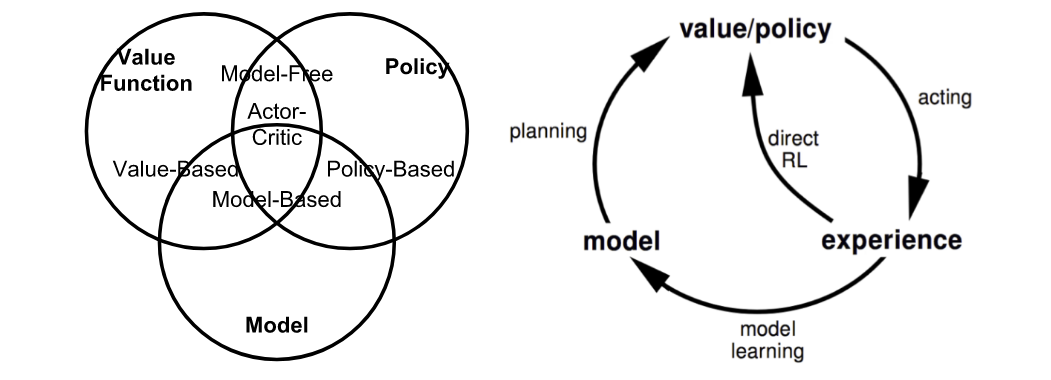图 2. 基于我们是否想要建模价值、策略或环境来总结 RL 中的方法。（图片来源：转载自 David Silver 的 RL 课程 lecture 1。）

智能体和环境之间的交互涉及一系列随时间推移的动作和观察到的奖励，t=1,2,…,T。在此过程中，智能体积累关于环境的知识，学习最佳策略，并决定接下来要采取哪个行动，以便有效地学习最佳策略。让我们将时间步 t 时的状态、行动和奖励分别标记为 St、At 和 Rt。因此，交互序列由一个episode（也称为“trial”或“trajectory”）完全描述，并且该序列在终端状态 ST 结束：

S1,A1,R2,S2,A2,…,ST

在深入研究不同类别的 RL 算法时，您会经常遇到的术语：

模型：转移和奖励

模型是环境的描述符。有了模型，我们可以学习或推断环境将如何与智能体互动并向智能体提供反馈。模型有两个主要部分，转移概率函数 P 和奖励函数 R。

假设当我们在状态 s 时，我们决定采取行动 a 以到达下一个状态 s' 并获得奖励 r。这被称为一个transition步骤，用一个元组 (s, a, s', r) 表示。

转移函数 P 记录了在采取行动 a 时，从状态 s 转移到 s' 并获得奖励 r 的概率。我们使用 P 作为“概率”的符号。

P(s′,r|s,a)=P[St+1=s′,Rt+1=r|St=s,At=a]

因此，状态转移函数可以定义为 P(s', r|s, a) 的函数：

Pss′a=P(s′|s,a)=P[St+1=s′|St=s,At=a]=∑r∈RP(s′,r|s,a)

奖励函数 R 预测由一个行动触发的下一个奖励：

R(s,a)=E[Rt+1|St=s,At=a]=∑r∈Rr∑s′∈SP(s′,r|s,a)

策略 (Policy)

策略，作为智能体的行为函数 π，告诉我们在状态 s 中采取哪个行动。它是从状态 s 到行动 a 的映射，可以是确定性的或随机的：

价值函数 (Value Function)

价值函数通过预测未来奖励来衡量一个状态的好坏，或者一个状态或行动有多大的回报。未来奖励，也称为return，是未来所有折扣奖励的总和。让我们计算从时间 t 开始的 return Gt：

Gt=Rt+1+γRt+2+⋯=∑k=0∞γkRt+k+1

折扣因子 γ∈[0,1] 会惩罚未来的奖励，因为：

状态 s 的状态价值是如果我们在时间 t 处于该状态时的预期 return，St=s：

Vπ(s)=Eπ[Gt|St=s]

类似地，我们将状态-动作对的行动价值（“Q-value”；我认为 Q 作为“质量”？）定义为：

Qπ(s,a)=Eπ[Gt|St=s,At=a]

此外，由于我们遵循目标策略 π，我们可以利用可能行动的概率分布和 Q 值来恢复状态价值：

Vπ(s)=∑a∈AQπ(s,a)π(a|s)

行动价值和状态价值之间的差异是行动优势函数（“A-value”）：

Aπ(s,a)=Qπ(s,a)−Vπ(s)

最优价值和策略

最优价值函数产生最大 return：

V∗(s)=maxπVπ(s),Q∗(s,a)=maxπQπ(s,a)

最佳策略实现最佳价值函数：

π∗=arg⁡maxπVπ(s),π∗=arg⁡maxπQπ(s,a)

当然，我们有 Vπ∗(s)=V∗(s) 和 Qπ∗(s,a)=Q∗(s,a)。

马尔可夫决策过程 (Markov Decision Processes)

更正式地说，几乎所有的 RL 问题都可以被构建为 Markov Decision Processes (MDPs)。MDP 中的所有状态都具有“马尔可夫”属性，指的是未来只依赖于当前状态，而不依赖于历史：

P[St+1|St]=P[St+1|S1,…,St]

或者换句话说，给定现在，未来和过去是条件独立的，因为当前状态封装了我们决定未来所需的所有统计信息。

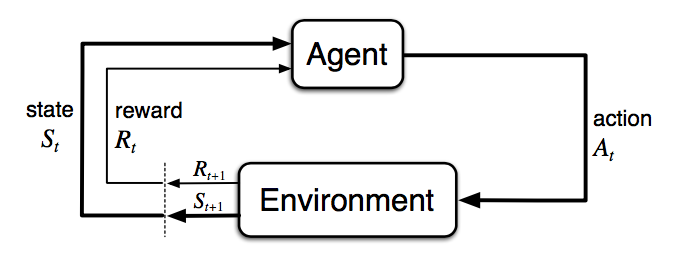图 3. 马尔可夫决策过程中的智能体-环境交互。（图片来源：Sec. 3.1 Sutton & Barto (2017)。）

马尔可夫决策过程由五个元素 M=⟨S,A,P,R,γ⟩ 组成，其中符号与 前面 部分中的关键概念具有相同的含义，与 RL 问题设置完全一致：

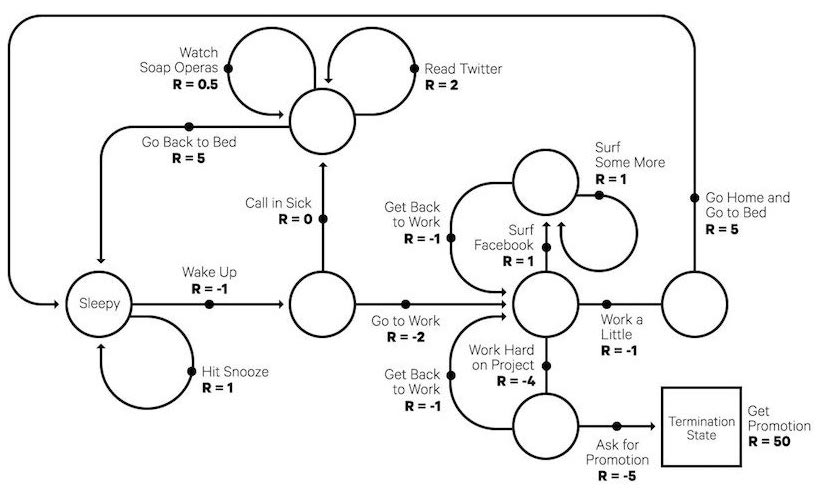图 4. 马尔可夫决策过程的一个有趣的例子：典型的工作日。（图片来源：randomant.net/reinforcement-learning-concepts）

贝尔曼方程 (Bellman Equations)

贝尔曼方程是指一组将价值函数分解为立即奖励加上折扣未来价值的方程。

V(s)=E[Gt|St=s]=E[Rt+1+γRt+2+γ2Rt+3+…|St=s]=E[Rt+1+γ(Rt+2+γRt+3+…)|St=s]=E[Rt+1+γGt+1|St=s]=E[Rt+1+γV(St+1)|St=s]

同样，对于 Q 值，

Q(s,a)=E[Rt+1+γV(St+1)∣St=s,At=a]=E[Rt+1+γEa∼πQ(St+1,a)∣St=s,At=a]

贝尔曼期望方程 (Bellman Expectation Equations)

递归更新过程可以进一步分解为建立在状态价值和行动价值函数上的方程。当我们进一步进入未来的行动步骤时，我们通过遵循策略 π 来交替扩展 V 和 Q。

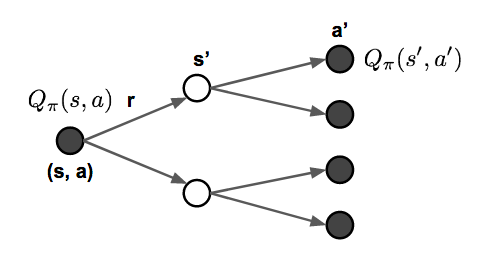图 5. 贝尔曼期望方程如何更新状态价值和行动价值函数的说明。

Vπ(s)=∑a∈Aπ(a|s)Qπ(s,a) Qπ(s,a)=R(s,a)+γ∑s′∈SPss′aVπ(s′) Vπ(s)=∑a∈Aπ(a|s)(R(s,a)+γ∑s′∈SPss′aVπ(s′)) Qπ(s,a)=R(s,a)+γ∑s′∈SPss′a∑a′∈Aπ(a′|s′)Qπ(s′,a′)

贝尔曼最优方程 (Bellman Optimality Equations)

如果我们只对最优价值感兴趣，而不是计算遵循策略的期望，我们可以直接进入交替更新期间的最大 return，而无需使用策略。回顾：最优价值 V∗ 和 Q∗ 是我们可以获得的最佳 return，定义在此处。

V∗(s)=maxa∈AQ∗(s,a) Q∗(s,a)=R(s,a)+γ∑s′∈SPss′aV∗(s′) V∗(s)=maxa∈A(R(s,a)+γ∑s′∈SPss′aV∗(s′)) Q∗(s,a)=R(s,a)+γ∑s′∈SPss′amaxa′∈AQ∗(s′,a′)

毫不奇怪，它们看起来与贝尔曼期望方程非常相似。

如果我们有关于环境的完整信息，这将变成一个规划问题，可以通过 DP 解决。不幸的是，在大多数情况下，我们不知道 Pss′a 或 R(s,a)，因此我们无法通过直接应用贝尔曼方程来解决 MDP，但它为许多 RL 算法奠定了理论基础。

常用方法

现在是时候回顾解决 RL 问题的主要方法和经典算法了。在未来的文章中，我计划进一步深入研究每种方法。

动态规划 (Dynamic Programming)

当模型完全已知时，遵循贝尔曼方程，我们可以使用 Dynamic Programming (DP) 来迭代地评估价值函数和改进策略。

策略评估 (Policy Evaluation)

策略评估是计算给定策略 π 的状态价值 Vπ：

Vt+1(s)=Eπ[r+γVt(s′)|St=s]=∑aπ(a|s)∑s′,rP(s′,r|s,a)(r+γVt(s′))

策略改进 (Policy Improvement)

基于价值函数，策略改进通过贪婪地行动来生成更好的策略 π′≥π。

Qπ(s,a)=E[Rt+1+γVπ(St+1)|St=s,At=a]=∑s′,rP(s′,r|s,a)(r+γVπ(s′))

策略迭代 (Policy Iteration)

广义策略迭代 (Generalized Policy Iteration, GPI) 算法是指在结合策略评估和改进时改进策略的迭代过程。

π0→evaluationVπ0→improveπ1→evaluationVπ1→improveπ2→evaluation⋯→improveπ∗→evaluationV∗

在 GPI 中，价值函数被重复近似以更接近当前策略的真实价值，与此同时，策略被重复改进以接近最优性。此策略迭代过程有效并且始终收敛到最优性，但为什么会这样呢？

假设我们有一个策略 π，然后通过贪婪地采取行动生成一个改进版本 π′，π′(s)=arg⁡maxa∈AQπ(s,a)。保证此改进的 π′ 的价值会更好，因为：

Qπ(s,π′(s))=Qπ(s,arg⁡maxa∈AQπ(s,a))=maxa∈AQπ(s,a)≥Qπ(s,π(s))=Vπ(s)

蒙特卡洛方法 (Monte-Carlo Methods)

首先，让我们回顾一下 V(s)=E[Gt|St=s]。蒙特卡洛 (MC) 方法使用一个简单的想法：它从原始经验的 episode 中学习，而无需对环境动态进行建模，并将观察到的平均 return 计算为预期 return 的近似值。为了计算经验 return Gt，MC 方法需要从完整的 episode S1,A1,R2,…,ST 学习以计算 Gt=∑k=0T−t−1γkRt+k+1 并且所有 episode 最终都必须终止。

状态 s 的经验平均 return 是：

𝟙𝟙V(s)=∑t=1T1[St=s]Gt∑t=1T1[St=s]

其中 𝟙1[St=s] 是一个二元指示函数。我们可以每次都计算状态 s 的访问次数，这样在一个 episode 中可能存在一个状态的多次访问（“every-visit”），或者只计算我们在一个 episode 中第一次遇到一个状态的次数（“first-visit”）。这种近似方式可以很容易地扩展到通过计算 (s, a) 对的行动价值函数。

𝟙𝟙Q(s,a)=∑t=1T1[St=s,At=a]Gt∑t=1T1[St=s,At=a]

为了通过 MC 学习最优策略，我们通过遵循与 GPI 类似的想法对其进行迭代。

  1. 相对于当前价值函数贪婪地改进策略：π(s)=arg⁡maxa∈AQ(s,a)。
  2. 使用新策略 π 生成一个新的 episode（即使用像 ε-greedy 这样的算法可以帮助我们在利用和探索之间取得平衡。）
  3. 使用新的 episode 估计 Q：𝟙𝟙qπ(s,a)=∑t=1T(1[St=s,At=a]∑k=0T−t−1γkRt+k+1)∑t=1T1[St=s,At=a]

时序差分学习 (Temporal-Difference Learning)

与蒙特卡洛方法类似，时序差分 (TD) 学习是无模型的，并从经验的 episode 中学习。但是，TD 学习可以从不完整的 episode 中学习，因此我们不需要跟踪 episode 直到终止。TD 学习非常重要，以至于 Sutton & Barto (2017) 在他们的 RL 书中将其描述为“一个想法……强化学习的核心和新颖之处”。

自举 (Bootstrapping)

TD 学习方法根据现有估计值更新目标，而不是像 MC 方法那样完全依赖于实际奖励和完整 return。这种方法被称为自举。

价值估计 (Value Estimation)

TD 学习中的关键思想是将价值函数 V(St) 更新为估计的 return Rt+1+γV(St+1)（称为“TD 目标”）。我们想要更新价值函数的程度由学习率超参数 α 控制：

V(St)←(1−α)V(St)+αGt V(St)←V(St)+α(Gt−V(St)) V(St)←V(St)+α(Rt+1+γV(St+1)−V(St))

类似地，对于行动价值估计：

Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,At+1)−Q(St,At))

接下来，让我们深入研究关于如何在 TD 学习中学习最优策略的有趣部分（又名“TD 控制”）。做好准备，你将在此部分看到许多经典算法的著名名称。

SARSA：On-Policy TD 控制

“SARSA”是指通过遵循 …,St,At,Rt+1,St+1,At+1,… 的序列更新 Q 值的过程。这个想法遵循 GPI 的相同路线。在一个 episode 中，它的工作方式如下：

  1. 初始化 t=0。
  2. 从 S0 开始，选择行动 A0=arg⁡maxa∈AQ(S0,a)，其中通常应用 ϵ-greedy。
  3. 在时间 t，在应用行动 At 之后，我们观察到奖励 Rt+1 并进入下一个状态 St+1。
  4. 然后以与步骤 2 相同的方式选择下一个行动：At+1=arg⁡maxa∈AQ(St+1,a)。
  5. 更新 Q 值函数：Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,At+1)−Q(St,At))。
  6. 设置 t=t+1 并从步骤 3 重复。

在 SARSA 的每一步中，我们需要根据_当前_策略选择_下一个_行动。

Q-Learning：Off-policy TD 控制

Q-learning 的开发是 Reinforcement Learning 早期的重大突破。[Watkins & Dayan, 1992]在一个 episode 中，它的工作方式如下：

  1. 初始化 t=0。
  2. 从 S0 开始。
  3. 在时间步 t，我们根据 Q 值选择行动，At=arg⁡maxa∈AQ(St,a)，并且通常应用 ϵ-greedy。
  4. 在应用行动 At 之后，我们观察到奖励 Rt+1 并进入下一个状态 St+1。
  5. 更新 Q 值函数：Q(St,At)←Q(St,At)+α(Rt+1+γmaxa∈AQ(St+1,a)−Q(St,At))。
  6. t=t+1 并从步骤 3 重复。

与 SARSA 的主要区别在于 Q-learning 不遵循当前策略来选择第二个行动 At+1。它从最佳 Q 值中估计 Q∗，但是哪个行动（表示为 a∗）导致此最大 Q 并不重要，并且在下一步中，Q-learning 可能不遵循 a∗。

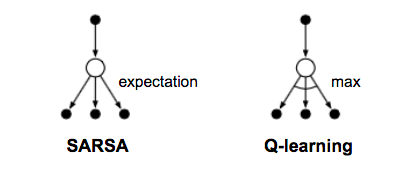图 6. Q-learning 和 SARSA 的备份图。（图片来源：根据 Sutton & Barto (2017) 中的图 6.5 重新绘制）

Deep Q-Network

理论上，我们可以像在一个巨大的表格中一样，记住 Q-learning 中所有状态-行动对的 Q∗(.)。但是，当状态和行动空间很大时，它很快变得在计算上不可行。因此，人们使用函数（即机器学习模型）来近似 Q 值，这称为函数近似。例如，如果我们使用带有参数 θ 的函数来计算 Q 值，我们可以将 Q 值函数标记为 Q(s,a;θ)。

不幸的是，当与非线性 Q 值函数近似和 自举 结合使用时，Q-learning 可能会出现不稳定和发散的问题。（参见 问题 #2）。

Deep Q-Network (“DQN”; Mnih et al. 2015) 旨在通过两种创新机制大大改进和稳定 Q-learning 的训练过程：

损失函数如下所示：

L(θ)=E(s,a,r,s′)∼U(D)[(r+γmaxa′Q(s′,a′;θ−)−Q(s,a;θ))2]

其中 U(D) 是回放记忆 D 上的均匀分布；θ− 是冻结目标 Q 网络的参数。

此外，还发现将误差项剪裁到 [-1, 1] 之间会有所帮助。（我总是对参数剪裁感到复杂，因为许多研究表明它在经验上有效，但它使数学变得不太漂亮。：/）

图 7. 具有经验回放和偶尔冻结的优化目标的 DQN 算法。预处理序列是在 Atari 游戏的输入图像上运行的某些过程的输出。不要太担心；只需将它们视为输入特征向量。（图片来源：Mnih et al. 2015）

DQN 有许多扩展可以改进原始设计，例如具有决斗架构的 DQN (Wang et al. 2016)，该架构使用共享网络参数估计状态价值函数 V(s) 和优势函数 A(s, a)。

结合 TD 和 MC 学习

在前面关于 TD 学习中价值估计的部分中，我们在计算 TD 目标时只进一步跟踪行动链中的一步。可以很容易地扩展它以采取多个步骤来估计 return。

让我们将遵循 n 步的估计 return 标记为 Gt(n),n=1,…,∞，然后：

n | Gt | 备注 ---|---|--- n=1 | Gt(1)=Rt+1+γV(St+1) | TD 学习 n=2 | Gt(2)=Rt+1+γRt+2+γ2V(St+2) … n=n | Gt(n)=Rt+1+γRt+2+⋯+γn−1Rt+n+γnV(St+n) … n=∞ | Gt(∞)=Rt+1+γRt+2+⋯+γT−t−1RT+γT−tV(ST) | MC 估计

广义 n 步 TD 学习仍然具有更新价值函数的相同形式：

V(St)←V(St)+α(Gt(n)−V(St))

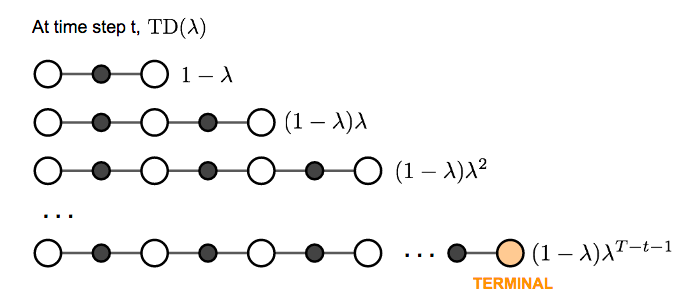
我们可以自由地在 TD 学习中选择任何我们喜欢的 n。现在的问题变成了什么是最佳 n？哪个 Gt(n) 给我们最好的 return 近似？一个常见但巧妙的解决方案是应用所有可能的 n 步 TD 目标的加权和，而不是选择单个最佳 n。权重按因子 λ 衰减，λn−1；这种直觉类似于为什么我们在计算 return 时想要折扣未来奖励：我们对未来的期望越高，我们的信心就越低。为了使所有权重 (n → ∞) 总和为 1，我们将每个权重乘以 (1-λ)，因为：

let S=1+λ+λ2+… S=1+λ(1+λ+λ2+…) S=1+λS S=1/(1−λ)

这种许多 n 步 return 的加权和称为 λ-return Gtλ=(1−λ)∑n=1∞λn−1Gt(n)。采用 λ-return 进行价值更新的 TD 学习被标记为 TD(λ)。我们在上面介绍的原始版本相当于 TD(0)。

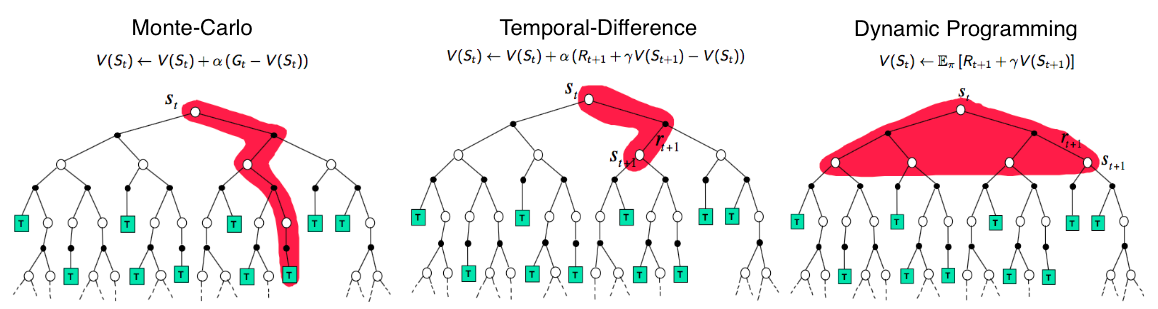图 8. 蒙特卡洛、时序差分学习和动态规划的状态价值函数备份图的比较。（图片来源：David Silver 的 RL 课程 lecture 4: "Model-Free Prediction"）

策略梯度 (Policy Gradient)

我们上面介绍的所有方法都旨在学习状态/行动价值函数，然后相应地选择行动。策略梯度方法改为使用相对于 θ, π(a|s;θ) 的参数化函数直接学习策略。让我们将奖励函数（损失函数的反面）定义为_预期 return_，并训练该算法以最大化奖励函数为目标。我的下一篇文章描述了策略梯度定理为何有效（证明），并介绍了一些策略梯度算法。

在离散空间中：

J(θ)=Vπθ(S1)=Eπθ[V1]

其中 S1 是初始起始状态。

或者在连续空间中：

J(θ)=∑s∈Sdπθ(s)Vπθ(s)=∑s∈S(dπθ(s)∑a∈Aπ(a|s,θ)Qπ(s,a))

其中 dπθ(s) 是 πθ 的马尔可夫链的平稳分布。如果您不熟悉“平稳分布”的定义，请查看此 参考。

使用_梯度上升_，我们可以找到产生最高 return 的最佳 θ。很自然地期望基于策略的方法在连续空间中更有用，因为在连续空间中存在无限数量的行动和/或状态来估计价值，因此基于价值的方法在计算上要昂贵得多。

策略梯度定理 (Policy Gradient Theorem)

_数值上_计算梯度可以通过在第 k 个维度上将 θ 扰动一个小的量 ε 来完成。即使 J(θ) 不可微，它也有效（太棒了！），但不出所料，速度非常慢。

∂J(θ)∂θk≈J(θ+ϵuk)−J(θ)ϵ

或者_分析上_，

J(θ)=Eπθ[r]=∑s∈Sdπθ(s)∑a∈Aπ(a|s;θ)R(s,a)

实际上，我们对（用 dπ(.) 替换 d(.)）有很好的理论支持：

J(θ)=∑s∈Sdπθ(s)∑a∈Aπ(a|s;θ)Qπ(s,a)∝∑s∈Sd(s)∑a∈Aπ(a|s;θ)Qπ(s,a)

查看 Sutton & Barto (2017) 中的第 13.1 节，了解为什么会这样。

然后，

J(θ)=∑s∈Sd(s)∑a∈Aπ(a|s;θ)Qπ(s,a) ∇J(θ)=∑s∈Sd(s)∑a∈A∇π(a|s;θ)Qπ(s,a) =∑s∈Sd(s)∑a∈Aπ(a|s;θ)∇π(a|s;θ)π(a|s;θ)Qπ(s,a) =∑s∈Sd(s)∑a∈Aπ(a|s;θ)∇ln⁡π(a|s;θ)Qπ(s,a) =Eπθ[∇ln⁡π(a|s;θ)Qπ(s,a)]

此结果被称为“策略梯度定理”，它为各种策略梯度算法奠定了理论基础：

∇J(θ)=Eπθ[∇ln⁡π(a|s,θ)Qπ(s,a)]

REINFORCE

REINFORCE，也称为蒙特卡洛策略梯度，依赖于 Qπ(s,a)，即 MC 方法使用 episode 样本估计的 return，以更新策略参数 θ。

REINFORCE 的一个常用变体是从 return Gt 中减去一个基线值，以减少梯度估计的方差，同时保持偏差不变。例如，一个常见的基线是状态价值，如果应用，我们将在梯度上升更新中使用 A(s,a)=Q(s,a)−V(s)。

  1. 随机初始化 θ
  2. 生成一个 episode S1,A1,R