seb-v About

引言

大家好！ 在这篇文章中，我将与大家分享在 AMD RDNA3 GPU 上编写优化的 FP32 矩阵乘法的步骤，其性能优于 rocBLAS 达 60%。我将涵盖一些基础知识，并解释我实现的所有优化。这将以迭代的方式在 8 个不同的 Kernel 中完成。

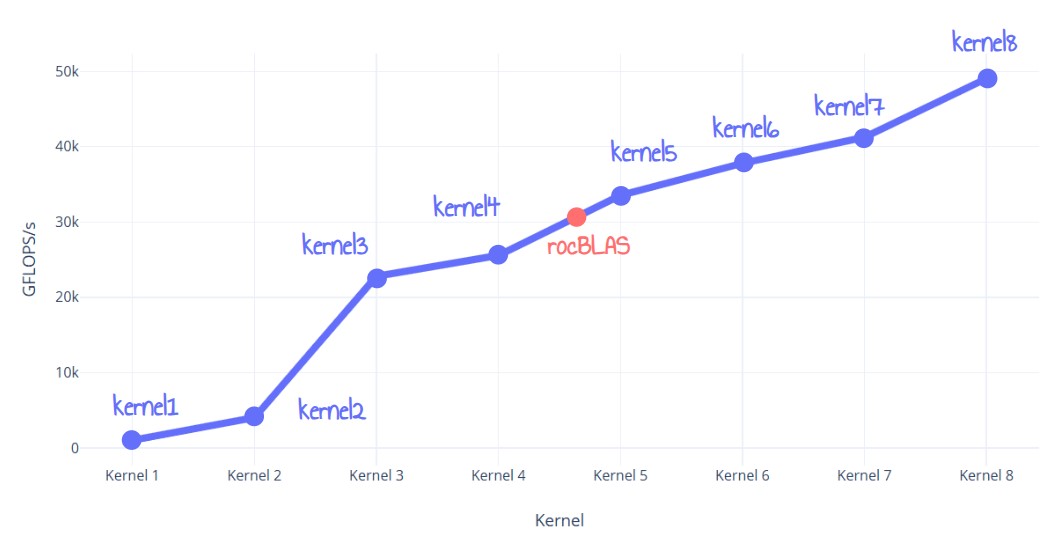图 1：性能结果抢先看

我最初打算通过这个项目来加深我对 RDNA3 的理解，并尝试 HIP，并且我觉得我需要分享我通过这样做学到的东西 :)。

在我们开始之前，我想说几件事：

• 我使用的所有信息都来自公开可用的 ISA 指南 1
• 我无意重新实现或替换 rocBLAS
• 为了简单起见，我只关注 4096x4096 矩阵的单精度 (FP32) 矩阵乘法。
• 我所有的测试都是在 Windows 11 上使用 AMD Radeon 7900 XTX 完成的。

话虽如此，让我们开始吧！

问题陈述

如今，在提高矩阵乘法性能方面有很多研究正在进行。作为 ML 应用程序中的核心算法，任何我们可以利用的 FLOPS 都是宝贵的。

在继续之前，让我们回顾一下矩阵乘法的基础知识。给定两个矩阵：

• 大小为 M,K 的 A
• 大小为 K,N 的 B

它们的乘积 C 计算如下：

Cij=∑k=0K−1Aik⋅Bkj i∈[0,M−1] j∈[0,N−1]

其中 C 是大小为 M,N 的结果矩阵。

对于矩阵 C 的每个输出值，我们计算矩阵 A 的行和矩阵 B 的列之间的点积。

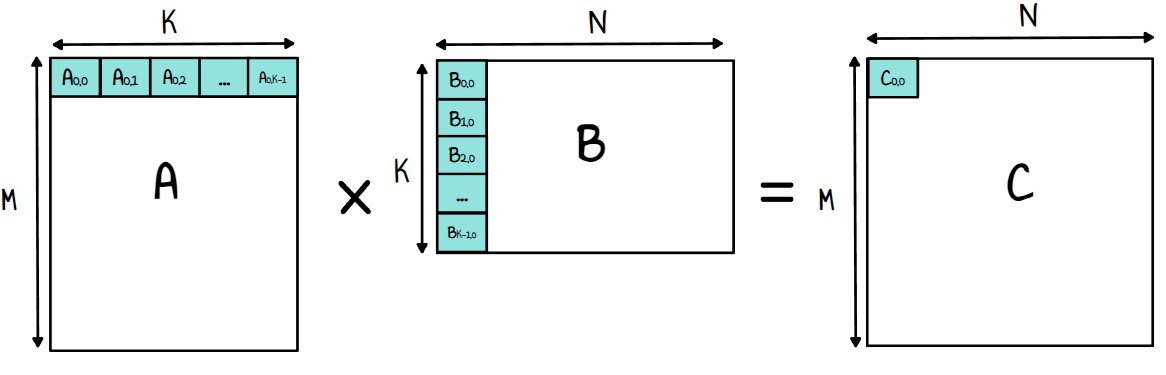图 2：C 的第一个元素的例子

在复杂度方面，我们有 O(n3) 的计算复杂度和 O(n2) 的内存访问。如果我们不考虑架构细节，这显然是一个计算密集型问题，我们的目标将是在 GPU 上达到计算密集型。

假设我们设法为 7900 XTX 编写了可能的最佳实现。它可以运行多快？为了回答这个问题，我们需要稍微了解一下 RDNA3 架构。

RDNA3 GPU 由 WorkGroup Processors (WGP) 阵列组成。每个 WGP 分成 2 个 Compute Units (CU)，它们自身又分成 2 个 SIMD。一个 SIMD 处理组织成 wave（或 CUDA 用户的 warp）的多个线程的工作，并具有一组组件来完成一些工作（如算术运算）。对于浮点运算，有两个 32 路 VALU 单元。

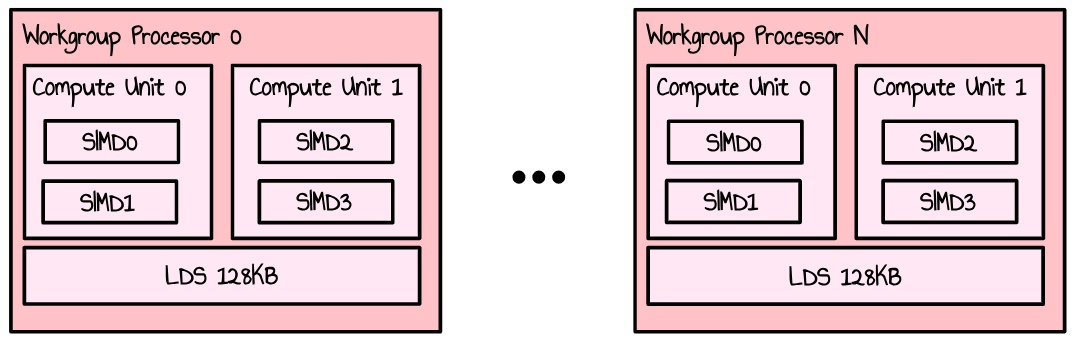图 3：WGP 的简化表示

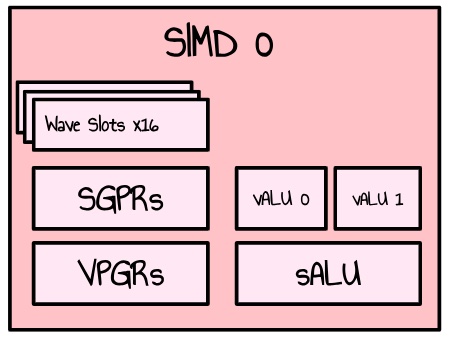图 4：单个 SIMD 的简化表示

我们可以用这个公式计算我们的理论每秒浮点运算次数：

FLOPS=freq∗nbSIMD∗flopsPerSIMD

每个 SIMD 可以在每个周期发出 2 个浮点指令（每个 vALU 单元上一个）。如果我们使用 FMA 指令 (Fused Multiply Add)，每个 SIMD 可以在每个周期发出 32*2*2=128 个浮点运算。7900 XTX 有 48 个 WGP，即 48*2*2=192 个 SIMD。

FLOPS=2500∗106∗192∗128FLOP/s FLOPS=61.44TFLOP/s

我们的理论 VRAM 带宽由以下公式给出：

BW=rate∗busWidth/8

7900 XTX 使用 GDDR6，具有 384 位总线，运行速度为 20 Gbps。

BW=20∗384/8=960GB/s

如果我们回到我们的 4096x4096 矩阵乘法，我们基本上需要做 2*4096*4096*4096 次运算。有了 61 TFLops 的实现，完成这项工作大约需要 2.23 毫秒，并且维持这个速率所需的带宽为 4096*4096*4*3/2.23*10−3=90.2GB/s。

当然，这些都是过于简化的计算，因为它们完全忽略了内存层次结构，但是我们看到可用的带宽足够高，因此我们可以增加我们读取的数据量，以更接近计算密集型。

Kernel 1：朴素的实现

让我们从一个朴素的实现开始，如下所示：

__global__ void kernel1_naive(const float *A, const float *B, float *C, int M, int K, int N, float alpha, float beta)
{
  int row = blockIdx.y * blockDim.y + threadIdx.y;
  int col = blockIdx.x * blockDim.x + threadIdx.x;
  if (row < M && col < N)
  {
    float acc_c = 0.0f; 
    for (int k = 0; k < K; ++k)
    {
      acc_c += A[row * K + k] * B[k * N + col];
    }
    C[row * N + col] = alpha * acc_c + beta * C[row * N + col];
  }
}

你会注意到我在这里做的是 C=alpha∗A∗B+beta∗C 而不是 C=A∗B。这是因为它更容易与 rocBLAS 之类的库进行比较，在这些库中，矩阵乘法由 SGEMM 函数（Single-Precision General Matrix Multiply）提供。

我们启动了 4096x4096 个线程，块大小为 16x16，每个线程计算之前描述的内部点积。

这个 kernel 的性能是 136 毫秒 (1010.60 GFlops/s)。我知道，这非常糟糕，远远低于我们 61 TFLops 的目标。

Kernel 0：rocBLAS 参考实现

现在我们已经看到了性能方面可能最差的实现，让我们看看官方的 rocBLAS 实现。

  const int M = N;
  const int K = N;
  CHECK_ROCBLAS_STATUS(rocblas_sgemm(
    handle,
    rocblas_operation_none, // Transpose option for A
    rocblas_operation_none, // Transpose option for B
    M,           // Number of rows in A and C
    N,           // Number of columns in B and C
    K,           // Number of columns in A and rows in B
    &alpha,         // alpha
    d_a,          // Matrix A on the device
    M,           // Leading dimension of A
    d_b,          // Matrix B on the device
    K,           // Leading dimension of B
    &beta,         // beta
    d_c,          // Matrix C on the device
    M            // Leading dimension of C
    ));

正如之前讨论的，我使用了 rocblas_sgemm 函数，并将 alpha 和 beta 设置为 1.02

这个 kernel 的性能是 4.49 毫秒 (30547 GFLOPs/s)。这显然比我们的 kernel 1 好得多，但仍然远低于我们理论上的 61.4 TFlops/s。

通过检查 RGP3 中的 ISA，我无法在 kernel 中找到任何双发射指令（只有 v_fmac_f32_e32）4

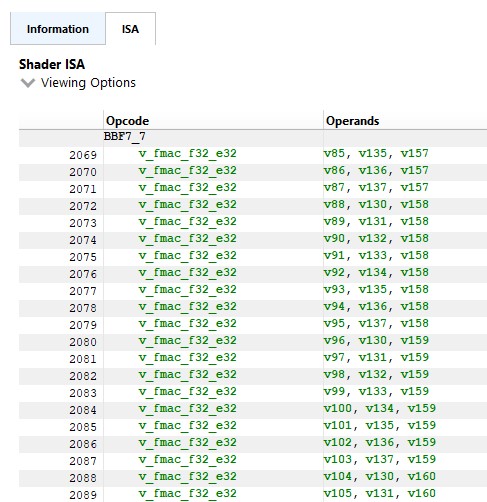图 5：rocBLAS ISA 代码的摘录

这非常令人惊讶，因为这实际上意味着其中一个 VALU 单元坐在那里什么也不做。

考虑到这一点，这个 kernel 的 VALU 利用率非常令人印象深刻，几乎达到 100%。然而，我们无法正确利用这些双发射指令，这确实令人惊讶。我稍后会讲到这一点。

Kernel 2：LDS 分块

我们的朴素 kernel 的主要问题是，我们的内部循环直接访问全局内存。这是低效的，因为从全局内存中获取数据具有很高的延迟，通常在数百个周期的数量级。由于每个内存读取之后是最小的计算（仅一次乘法和一次加法），因此即使有大量并发线程，GPU 也难以隐藏这种延迟。此外，该算法在不同的线程中重复读取来自全局内存的相同行和列，导致冗余内存访问，并进一步加剧了性能瓶颈。

解决这个问题的一种方法是将数据一次性加载到更快的本地内存中，然后所有线程高效地迭代它。在 RDNA3 上，我们有 Local Data Store (LDS)，这是一种高速、低延迟的内存，可由工作组中的所有线程访问。

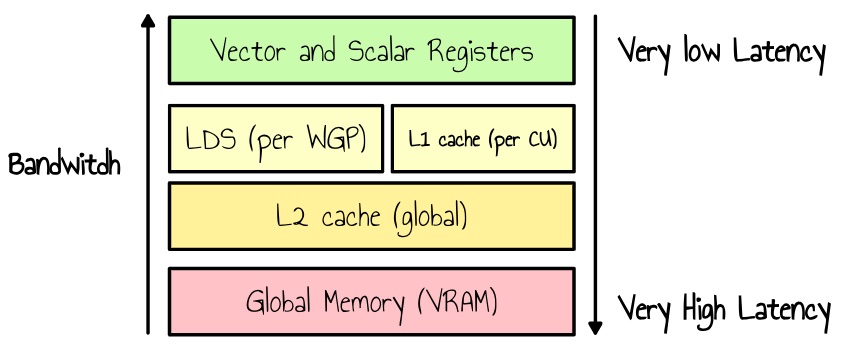图 6：内存层次结构的简化表示

由于 LDS 的容量比全局内存小得多，我们需要使用分块将我们的问题分成更小的子矩阵乘法。一种促进这一点的方法是通过将内部循环的点积移动到外部循环来重构计算。关键思想是缓存矩阵 A 的一列和矩阵 B 的一行，然后在整个 tile 上执行计算。这种方法更具缓存效率，并显著降低内存访问延迟。

我们的 kernel 1 的伪代码是：

for i from 0 to M - 1:         # Loop over rows of A
  for j from 0 to N - 1:       # Loop over columns of B
    sum = 0             
    for k from 0 to K - 1:     # Loop over columns of A / rows of B
      sum += A[i][k] * B[k][j] 
    end for
    C[i][j] = sum          
  end for
end for

如果我们把点积移到外部循环，我们有：

for k from 0 to K - 1:         # Outer loop over the shared dimension
  for i from 0 to M - 1:       # Loop over rows of A
    for j from 0 to N - 1:     # Loop over columns of B
      C[i][j] += A[i][k] * B[k][j] 
    end for
  end for
end for

这种形式的分块很简单：每个工作组在 tile 上运行并遵循以下步骤：（BK 是批量大小，即我们加载到 LDS 的行/列数）

Init c to 0 
While kId is less than N:
 # Load A and B to Tile As and Bs
 Load BK columns A to As
 Load BK rows to Bs
 Syncthreads
 # Accumulate results using LDS
 for k from 0 to BK
  c += As[threadIdx.y][k] * Bs[k][threadIdx.x]
 Syncthreads
 Increment kId by BK
end for
c[row][col]=c

如果我们选择一个 32x32 的 tile 大小和 BK=32，我们的新 kernel 如下所示：

#define TILE_SIZE 32
__global__ void kernel2_lds(const float *A, const float *B, float *C, int N)
{
  __shared__ float As[TILE_SIZE][TILE_SIZE];
  __shared__ float Bs[TILE_SIZE][TILE_SIZE];
  int row = blockIdx.y * TILE_SIZE + threadIdx.y;
  int col = blockIdx.x * TILE_SIZE + threadIdx.x;
  float sum = 0.0f;
  for (int t = 0; t < N; t += TILE_SIZE)
  {
    Bs[threadIdx.y][threadIdx.x] = B[N * (threadIdx.y + t) + col];
    As[threadIdx.y][threadIdx.x] = A[N * row + t + threadIdx.x];
    __syncthreads();
    for (int k = 0; k < TILE_SIZE; k++)
    {
      sum += As[threadIdx.y][k] * Bs[k][threadIdx.x];
    }
    __syncthreads();
  }
  if (row < N && col < N)
  {
    C[row * N + col] = sum;
  }
}

这里需要 __syncthreads(); 来确保工作组中的所有线程都可以看到加载到 LDS 中的数据，并在对数据进行任何更新之前进行同步。

我们还确保矩阵 A 和 B 的内容都按行而不是按列加载到 LDS 中，以避免非合并的内存访问。实际上，如果我们按列读取，则 wave 中的每个线程将访问一个非连续的内存区域，从而导致多个单独的事务并降低效率，如下面的两个图所示。

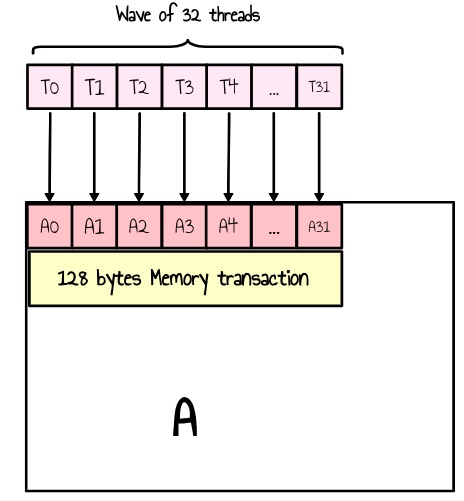图 7：矩阵 A 的合并加载。所有线程的单个 128 字节内存事务

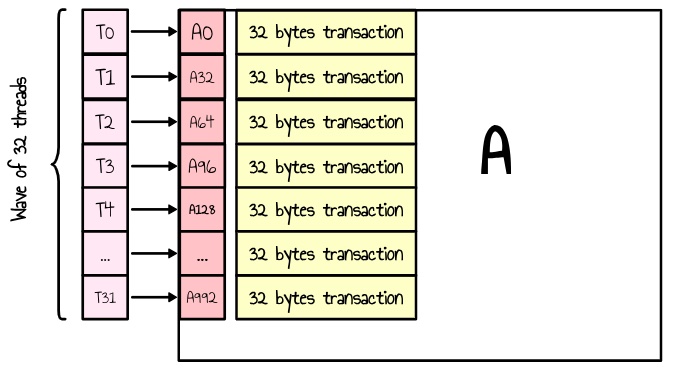图 8：矩阵 A 的非合并加载。单个 wave 的多个 32 字节内存事务

根据 ISA 指南，设备内存通过 32、64 或 128 字节的事务进行访问，这些事务必须自然对齐。最大化内存吞吐量需要在 wave 内的线程之间合并内存访问，以最小化事务的数量5。

这个 kernel 的性能是 34.2 毫秒 (4017 GFlops/s)。比我们朴素的 kernel 快 4 倍！

| Kernel # | Description | Time (ms) | Performance (GFLOPS) | Relative Performance to rocBLAS | | --------- | -------------- | --------- | -------------------- | ------------------------------- | | Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % | | Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % | | Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % |

让我们使用 RGP 来了解发生了什么。我们的占用率非常好（100 %），但是我们的 VALU 利用率仅为 15%。

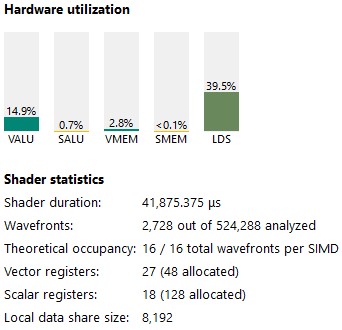图 9：从 RGP 的指令选项卡中获取的统计信息

如果我们查看指令计时选项卡中的 ISA，我们会看到几个有趣的事情：

• 内部循环已展开
• 我们没有使用 v_dual_fmac_f32，只有 v_fmac_f32，就像 rocBLAS 一样
• 我们在这些 LDS 加载上获得持续的 90 个周期停顿（未隐藏）（检查 s_waitcnt lgkmcnt(X) 指令）

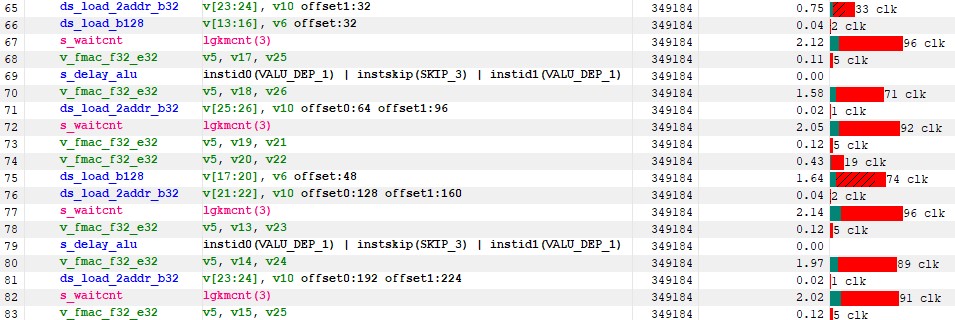图 10：指令计时

为了理解发生了什么，我们需要快速解释 SIMD 调度的工作原理。在每个时钟周期中，SIMD 从 wave 池中选择一条指令来发射。一个 SIMD 可以并行管理多达 16 个 wavefront。当我们提到占用率时，我们实际上是在谈论活动 wave 与 SIMD 可以支持的理论最大 wave 数之比。活动 wavefront 越多，SIMD 可以在 wave 之间切换的可能性越大，从而增加了隐藏单个 wavefront 内延迟的机会 6。

如果我们回到我们的案例，我们可能遇到这样的情况：

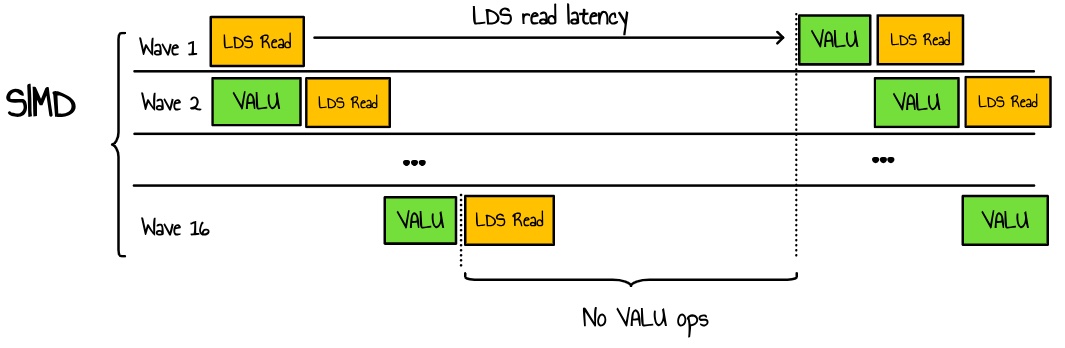图 11：SIMD 中的 wavefront 调度

在这里，我们有一个高占用率的 kernel，并行启动了许多 wave，所有这些 wave 都在争夺对 LDS 的访问。由于我们的 VALU 操作所花费的时间比 LDS 延迟短，因此即使有额外的线程，也无法隐藏延迟。这会导致 LDS 带宽拥塞和由于延迟而导致的资源浪费。

解决这个问题的一种方法是增加我们 kernel 的算术强度，确保每个 wave 的 VALU 操作比 LDS 内存读取花费更长的时间。

Kernel 3：寄存器分块

现在，我们想要增加我们 kernel 的算术复杂度。这意味着让每个线程执行更多的计算。本质上，我们的目标是增加计算与数据读取的比率。实现这一点的一种方法是计算每个线程的一个小输出 tile - 例如，一个 8x8 的 tile。为此，我们引入了额外的分块级别。

每个线程将负责生成输出矩阵的一个小 tile。我们可以将矩阵 A 和 B 的内容缓存到寄存器中，以实现非常低的延迟访问。但是，寄存器在 GPU 上的数量有限，每个 SIMD 有 1536 个 VGPR（Vector General-Purpose Registers）可用，每个 kernel 最多 256 个寄存器。增加寄存器使用意味着我们将无法为每个 SIMD 启动尽可能多的 wave，从而有效地降低占用率。但是，如果我们仅用几个 wave 就可以最大化 SIMD 的 VALU（Vector Arithmetic Logic Units）的利用率，这应该不是问题。

现在，让我们看看不同的分块级别：

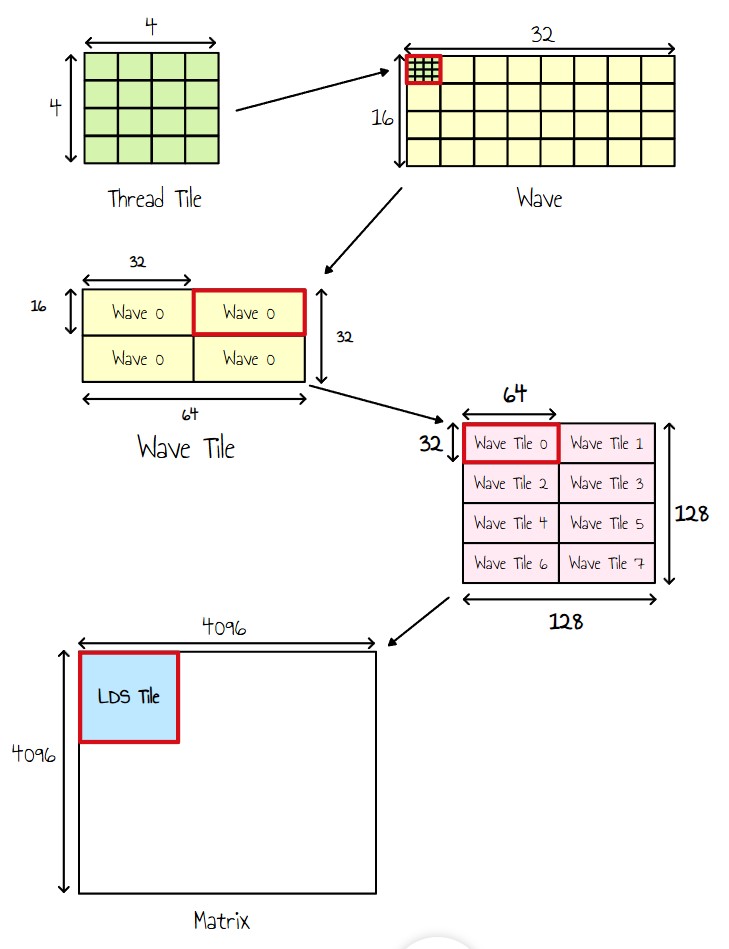图 12：分块级别

• 每个线程现在输出一个 4x4 的块（Thread Tile）。
• 由于一个 wave 由 32 个线程组成，我们将它们组织成一个 8x4 的块，使单个 wave 负责输出一个 32×16 的 tile。
• 鉴于我们每个工作组有 256 个线程（即 8 个 wave），我们将它们排列成一个 2×4 网格的 Wave Tile。
• 每个 wave 迭代一个 2x2 的网格以覆盖整个 Wave Tile。

本质上，这意味着每个线程现在将负责计算一个 8x8 的输出 tile。

我们的 kernel 参数如下所示：

  #define BLOCK_SIZE 256
  // Block Tile size
  constexpr int BN = 128;
  constexpr int BM = 128;
  // Number of Row or column we read per batch
  constexpr int BK = 8; 
  // Thread Tile size . 4x4
  constexpr int TN = 4;
  constexpr int TM = 4;
  // A wave is a block of 8x4 of the output matrix
  constexpr int nbThreadXPerWave = 8;
  constexpr int nbThreadYPerWave = 4;
  // Number of waves in a block
  constexpr int nbWavesPerBlock = BLOCK_SIZE / 32;
  constexpr int WN = 64;
  constexpr int WM = BN * BM / nbWavesPerBlock / WN;
  constexpr int nbIterWaveN = WN / (nbThreadXPerWave * TN);
  constexpr int nbIterWaveM = WM / (nbThreadYPerWave * TM);
  // LDS Tile
  __shared__ float As[BK][BM];
  __shared__ float Bs[BK][BN];
  
  // Column and row from A and B, stored into registers
  float A_col[nbIterWaveM * TM];
  float B_row[nbIterWaveN * TN];
  //Wave Tile (registers)
  float C_regs[TM * nbIterWaveM * TN * nbIterWaveN] = {0.0f};

我们新 kernel 的伪代码：

  Initialize kId to 0
  While kId is less than N:
    # Loading Tile to LDS
    Load BK columns from A to As
    Load BK rows from B to Bs
    Syncthreads
    For k from 0 to BK - 1 do:
      Load col k of As to A_col
      Load row k of Bs to B_row
      # Wave Tile
      For idY from 0 to nbIterWaveM:
       For idX from 0 to nbIterWaveN:
        # Thread Tile
        For i from 0 to TM:
         For j from 0 to TN:
           x = idX * TN + j;
           y = idY * TM + i;
           C_regs[y][x] = A_col[y] * B_row[x]
    Syncthreads
    Increment kId by BK
  Write C_regs to C

完整的 kernel 源代码可以在这里找到。

这个 kernel 的性能是 6.03 毫秒 (22777 GFlops/s)，比我们之前的 kernel 快 5 倍！

| Kernel # | Description | Time (ms) | Performance (GFLOPS) | Relative Performance to rocBLAS | | --------- | ---------------------- | --------- | -------------------- | ------------------------------- | | Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % | | Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % | | Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % | | Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % |

我们的占用率较低，但 VALU 利用率显著提高。

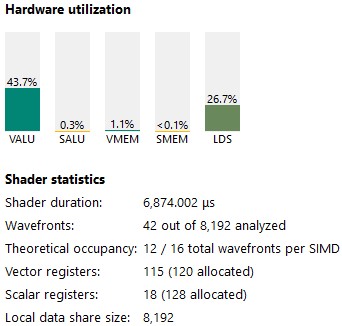图 13：kernel 3 统计信息

ISA 看起来不错。我们现在有很多 v_dual_fmac 指令 - 正是我们想要的，即使有些仍然是单个 fma。

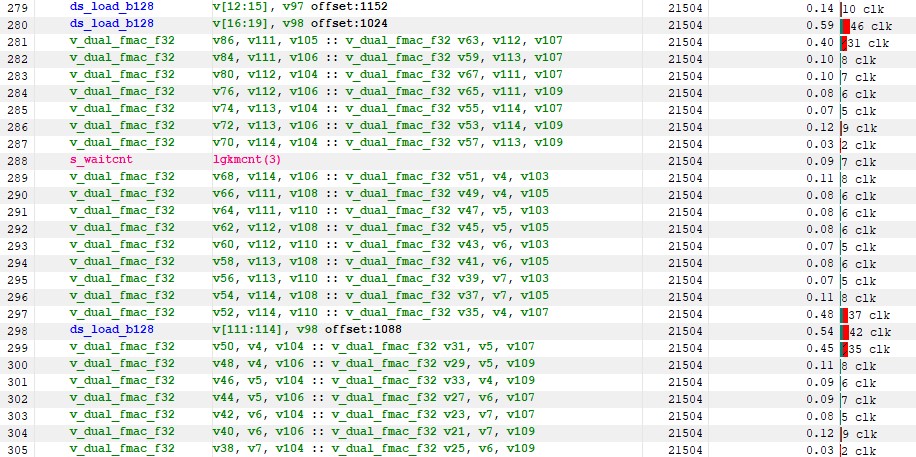图 14：kernel 3 指令计时

尽管这比 Kernel 2 有了显著改进，但我们仍然可以看到我们正在等待 LDS。对于第一批 ds_load 指令来说尤其如此，我们在下面看到超过 100 个时钟周期的累积非隐藏延迟：

图 15：ds_load 指令延迟

在深入研究这个问题之前，我们需要首先改进我们从全局内存读取的方式。根据 RGP，这现在是性能方面最大的瓶颈。

图 16：gmem 等待延迟

我们全局内存等待的累积延迟超过 1200 万个时钟周期，是内部循环中 LDS 加载等待的四倍多。

为了进一步优化性能，我们将专注于更好地隐藏全局内存读取延迟。

Kernel 4：GMEM 双缓冲

使用我们当前的实现，每个 wave 必须等待全局内存，然后等待 LDS 写入延迟才能执行任何工作。在高占用率的情况下，如果 GPU 可以找到其他 wave 来隐藏这种延迟，这应该不是问题。但是，在实践中，我们经常有多个 wave 同时处于相同的状态运行，因为我们在从全局内存读取之前和之后使用同步线程。

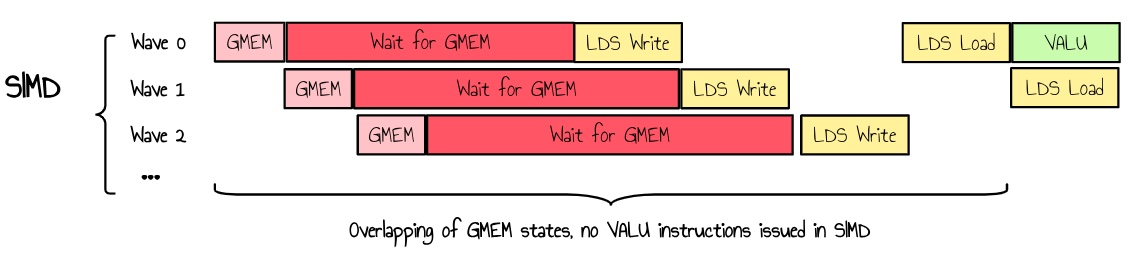图 17：多个 wave 等待 GMEM 加载

缓解这种情况的一种方法是使用双缓冲。我们可以分配两倍的内存，并并行执行对 LDS 的读取和写入。

或者，我们可以使用中间寄存器从全局内存加载数据，同时处理 LDS，仅在需要之前才写入 LDS。这确保了不等待全局内存。

我现在更喜欢这种方法，因为我暂时不想在内部循环中引入额外的 LDS 压力。

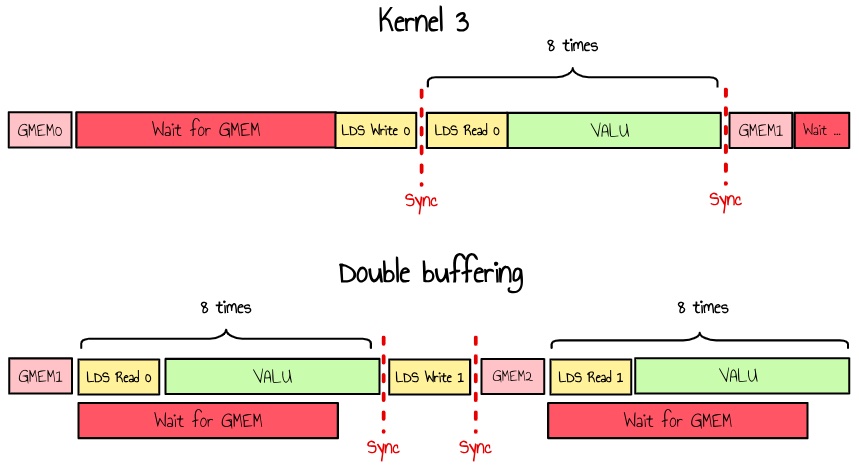图 18：GMEM 加载上的双缓冲

如果我们更新我们的伪代码，我们现在有：

  Initialize kId to 0
  # Load first batch before loop
  Load BK columns from A to As
  Load BK rows from B to Bs
  Syncthreads
  While kId is less than N:
    # Loading Tile to LDS
    Load BK columns from A to A_TMP (no wait)
    Load BK rows from B to B_TMP (no wait)
    For k from 0 to BK - 1 do:
      Load col k of As to A_col
      Load row k of Bs to B_row
      # Wave Tile
      For idY from 0 to nbIterWaveM:
       For idX from 0 to nbIterWaveN:
        # Thread Tile
        For i from 0 to TM:
         For j from 0 to TN:
           x = idX * TN + j;
           y = idY * TM + i;
           C_regs[y][x] = A_col[y] * B_row[x]
    Syncthreads
    Save A_TMP and B_TMP to As and Bs
    Syncthreads
    Increment kId by BK
  Write C_regs to C

令我惊讶的是，这个 kernel 的性能下降到 14.3032 毫秒 (9612.48 GFLOPS)，比 kernel 3 慢了 2 倍多！

我们的双缓冲算法利用了更多的寄存器并降低了占用率。在检查 RGP 中的 ISA 后，我们看到 HIP 编译器试图通过使用 scratch memory 来保持较低的寄存器使用率 - 这对性能不利 7。

图 19：引入了 scratch_load 指令以减少寄存器使用

不幸的是，我们无法在 HIP 中直接设置每个 kernel 的最大寄存器数（理论上为 256）。但是，我们可以使用 launch_bounds 扩展来为编译器提供提示。

有了这个改变，性能又恢复正常了：5.37 毫秒 (25559.6 GFLOP/s)。

完整的 kernel 源代码可以在这里找到。

| Kernel # | Description | Time (ms) | Performance (GFLOPS) | Relative Performance to rocBLAS | | --------- | ------------------------ | --------- | -------------------- | ------------------------------- | | Kernel 0 | rocBLAS | 4.4992 | 30547.4 | 100.0 % | | Kernel 1 | Naive version | 136.006 | 1010.54 | 3.3 % | | Kernel 2 | LDS tiling | 34.2059 | 4017.99 | 13.1 % | | Kernel 3 | Register tiling | 6.0341 | 22777.0 | 74.6 % | | Kernel 4 | GMEM Double buffer | 5.3772 | 25559.6 | 83.7% |

VALU 利用率从 43 % 增加到 52 %。

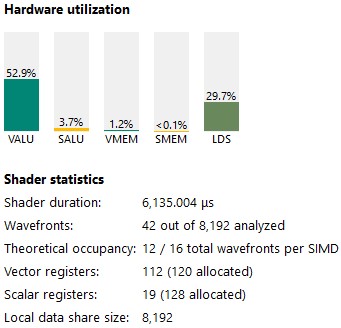图 20：kernel 4 统计信息

我们现在可以回到内部循环中的 LDS 加载，这些加载已成为新的瓶颈，如下所示。

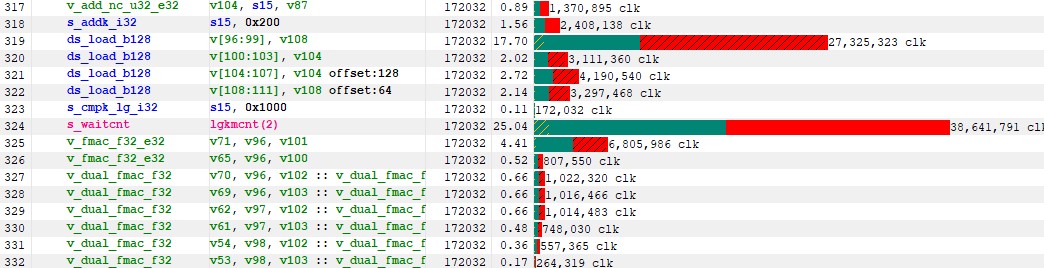图 21：LDS 加载上的延迟

Kernel 5：优化 LDS 使用

我在之前的 kernel 中没有注意到的一件事是我们在 LDS 上是否有 bank 冲突。实际上，此信息不易在 RGP 中访问。如果我们查看我们写入 LDS 的 ISA 部分，我们会发现延迟出乎意料地高。

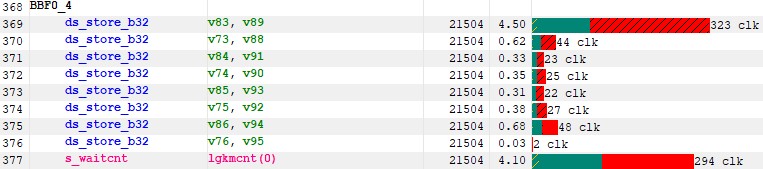图 22：LDS 写入上的延迟

根据 RDNA3 编程指南，LDS 内存被分成 64 个 DWORD 宽的 RAM bank。这 64 个 bank 又被细分为两组 32 bank，其中 32 个 bank 与一对 SIMD32 相关联，另外 32 个 bank 与 WGP 中的另一对 SIMD32 相关联。每个 bank 都是一个 512x32 的双端口 RAM（每个时钟周期 1R/1W）。DWORD 以串行方式放置在 bank 中，但所有 bank 都可以同时执行存储或加载1。

因此，如果 wave 中的线程访问相同的 bank，则内存事务将被序列化，这正是我们向 As 写入矩阵 A 的列时发生的情况。

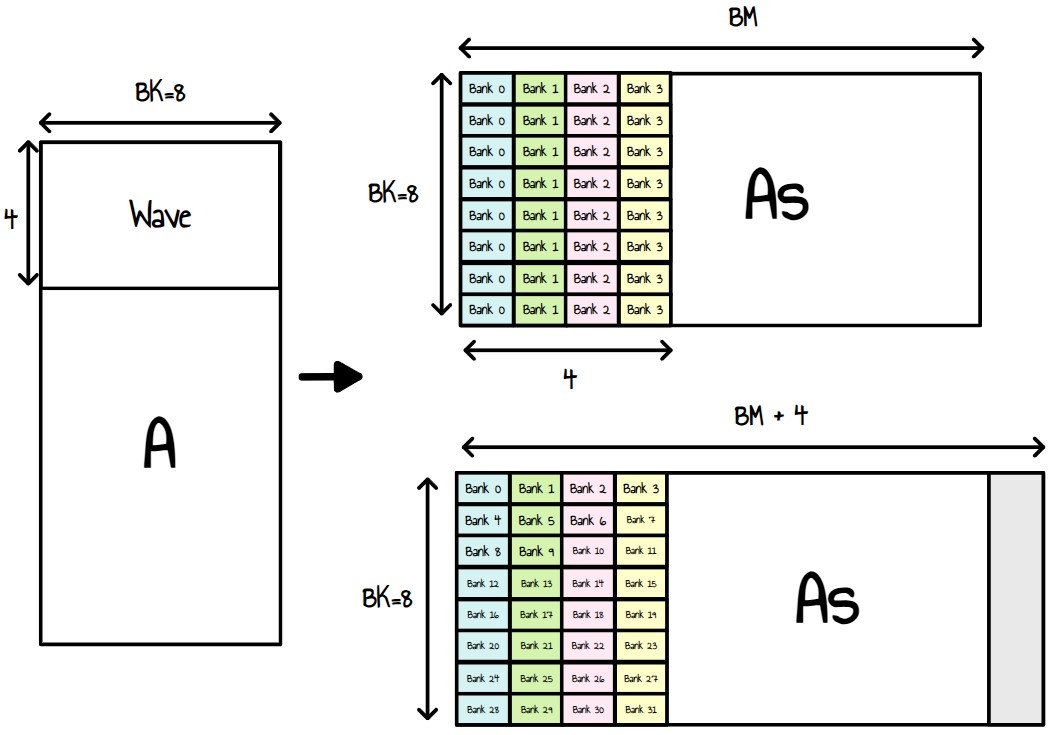图 23：矩阵 A bank 冲突以及如何消除它们

我们当前的 kernel 按行读取矩阵 A 的内容，以避免非合并的内存加载。鉴于我们随后对矩阵 A 的列进行操作，我们将矩阵 A 转置到矩阵 As 中，以便 As 的每一行对应于 A 的 tile 列。

现在，如果我们看看这项工作如何映射到 wave，我们就会看到我们基本上在每个 wave 中将 8 次写入到 4 个连续的 bank。解决这个问题的一种方法是在我们的 LDS 矩阵 As 中添加 4 个元素的填充。

__shared__ float As[BK][BM+4]; // 4 padding to avoid bank conflicts

使用此更改再次进行 RGP 捕获：

图 24：使用填充更新的延迟

LDS 延迟已大大降低，并且我们的 VALU 利用率现在为 62.3%。

但是，我们的 kernel 仍然受这些 LDS 加载的限制。让我们做一些餐巾纸数学，并检查我们是否没有达到 LDS 带宽的限制。

如前所述，每对 SIMD 都有一个 32 bank 的内存，能够读取 DWORD。我们的理论带宽应该是这样的：

BW=nbSIMD/2∗32∗4∗freq BW=96∗32∗4∗2.371∗109 BW=29.1TBytes/s

现在，让我们分析一下我们当前的算法所做的事情：

• 每个线程在每次迭代中读取每个矩阵 8 个 DWORDS（相当于 8x8 的 Thread tile）
• 一个 wave 总共读取 32x8x2 DWORDS
• 我们的工作组有 8 个 wave，所以每次迭代有 4096 次读取。
• 鉴于我们有 4096 次迭代，我们为每个工作组读取 4096x4096x4 字节。
• 对于 32x32 的工作组，总共有 68719476736 字节。

这是用于读取的。我们还写入 LDS：4096x128x32x32x4x2 = 4294967296 字节。

以我们当前的 5.37 毫秒的执行时间为例，所需的 LDS 带宽约为 13.56 TBytes/s。这不到最大容量的 46%，但是我们的 kernel 很可能在多个 wave 尝试同时读取或写入时遇到 LDS 拥塞。

为了缓解这种情况，我们可以尝试以下两件事：

• 启用 CU 模式
• 再次增加我们的算术强度，以换取 LDS 读取与 GMEM 读取

根据 RDNA3 编程指南，LDS 可以在 2 种不同的模式下运行：WGP 模式和 CU 模式。HIP 默认使用 WGP 模式。在 WGP 模式下，LDS 是一个所有 WGP 上的 wave 都可以访问的大型连续内存，这意味着我们更有可能在 LDS 上遇到拥塞。在 CU 模式下，LDS 有效地分为单独的上下 LDS，每个 LDS 为两个 SIMD32 提供服务。Wave 在与其运行 SIMD 关联的 LDS 的一半内分配 LDS 空间。通过启用 CU 模式，我们应该减少 wave 争夺 LDS 的可能性 8

我们可以尝试的第二件事是将我们的 Thread tile 增加到 16x8 而不是 8x8。这将提高计算与数据读取的比率。它仍然应该适合我们 kernel 的 256 VGPR 预算，并将我们的带宽要求降低到 10.3 TBytes/s

通过所有这些更改，此 kernel 的性能现在为 4.09 毫秒 (33526 GFLOP/s)。这比 rocBLAS 更好！

完整的 kernel 源代码可以在[这里](https://seb-v.github.io/optimization/update/2025/01/2