GATE：AI 和自动化场景探索器
Publications & Commentary
Publications Gradient Updates Epoch After Hours
Data & Resources
Data on AI AI Trends & Statistics Data Insights
Projects
FrontierMath GATE Playground Distributed Training
About
Our Team About Our Research Careers Our Funding
Contact
Search epoch.ai
Search
Enter a query to search for results
Previous
1
...
2
...
3
Next
Cite this work as
Ege Erdil, Andrei Potlogea, Tamay Besiroglu, Edu Roldan, Anson Ho, Jaime Sevilla, Matthew Barnett, Matej Vrzala, and Robert Sandler. ‘GATE: An Integrated Assessment Model for AI Automation`. _ArXiv [econ.GN]_, 2025. arXiv. https://arxiv.org/abs/2503.04941.
BibTeX citation
@misc{erdil2025gateintegratedassessmentmodel,
title={GATE: An Integrated Assessment Model for AI Automation},
author={Ege Erdil and Andrei Potlogea and Tamay Besiroglu and Edu Roldan and Anson Ho and Jaime Sevilla and Matthew Barnett and Matej Vrzla and Robert Sandler},
year={2025},
eprint={2503.04941},
archivePrefix={arXiv},
primaryClass={econ.GN},
url={https://arxiv.org/abs/2503.04941},
}
GATE — AI 和自动化场景探索器
编辑参数 AI and ComputeInvestmentAI AutomationEconomic Growth 文档
AI 和计算
GATE 模型的核心概念是 有效计算力 – 用于训练和运行 AI 系统的计算预算，并根据算法随时间的改进进行调整。有效计算力的增长可以分解为三个部分：计算硬件的增长、硬件效率的提高以及软件效率的提升。 模型一致性检查失败——结果可能不可靠。
最大训练运行
Physical FLOPEffective FLOP A: Full automationB: Full automationGPT-2GPT-42020202520302035204020451020102510301035YearPhysical FLOPAB CC-BY | epoch.ai
硬件效率
20252027202920312033203520372039204120432045101910201021YearFLOP/year/$AB CC-BY | epoch.ai
软件效率
2025202720292031203320352037203920412043204510100103YearEffective FLOP per FLOPAB CC-BY | epoch.ai
推理-训练分割 Simulation A Simulation B
202520272029203120332035203720392041204320450%20%40%60%80%100%YearPercentageInferenceTraining CC-BY | epoch.ai
芯片制造规模扩大
202520272029203120332035203720392041204320451100104106YearProduction scale-upAB CC-BY | epoch.ai
投资
GATE 预测 AI 相关资本和研发方面的高水平投资，以支持有效计算力的大规模扩张。这涉及从传统资本投资和消费中进行重大重新分配，并且发生在 AI 产生显着经济价值之前，其动机是 AI 自动化带来的巨大回报。 模型一致性检查失败——结果可能不可靠。
有效计算力储备的投资
AI 投资和产生的经济价值
储蓄率
传统资本投资
计算投资吸引力
AI 自动化
GATE 模型将给定的有效计算力转化为一定程度的 AI 自动化。这通过扩大可以自动化的任务的比例以及增加已自动化的任务的有效运行时计算来实现。广泛的自动化通常发生在模拟开始后的二十年内。 模型一致性检查失败——结果可能不可靠。
自动化任务的比例
新自动化的任务
运行时计算分布
收入的劳动份额
人力劳动的边际产量
经济增长
随着自动化任务比例的增加，就有可能在越来越多的任务中替代人力劳动。由于有效计算力的扩展速度远快于人力劳动，因此这导致了有效劳动力规模的急剧扩大——从而导致经济增长率的急剧提高。 模型一致性检查失败——结果可能不可靠。
世界总产值 (GWP)
产出增长
有效工人数量
资本存量增长
按自动化程度划分的增长率
文档
概述
增长和 AI 转型内生 (GATE) 模型是一个用于评估 AI 发展对经济影响的综合模型。 为了配合我们的论文详细描述 GATE 模型，我们开发了一个 playground，让感兴趣的读者可以修改参数设置并观察模型在各种场景下的行为。 本文档描述了以下内容：
- GATE 模型的结构、实施和求解的简明摘要。
- 如何使用 GATE playground 并解释其预测。
- playground 的默认参数设置的解释。
如果您想提出任何问题或提供有关 GATE playground 的反馈，可以通过 info@epoch.ai 与我们联系。您还可以阅读我们的配套博客文章，了解该模型提出的关键结果的概述。
模型结构
GATE 的核心动态是一个自动化反馈循环：投资驱动用于训练和部署越来越强大的 AI 系统的计算量的增加，这反过来又导致逐渐自动化当前由人类执行的任务。这反过来又增加了产出，从而为进一步投资 AI 发展提供了更多资源。该模型由三个模块组成，如下图所示：
计算
AI 投资被分配用于增加 “有效计算力” 的储备，然后可以用于训练或运行 AI 系统。这是 物理计算力（即在物理设备中运行的计算机操作的数量）和考虑 AI 算法改进的 软件效率 因素的乘积。 物理计算力的增加源于硬件效率的提高和芯片储备的扩大。这两者都增加了每年可以执行的物理计算机操作的数量。 作为对物理计算力的补充，软件效率描述了计算用于训练或运行 AI 系统的效率。软件效率的提高产生了类似于更多物理计算力带来的性能改进——即软件效率的翻倍带来了相当于物理计算力翻倍的性能改进。因此，我们使用“有效计算力”的概念来衡量社会整体的计算资源。 计算基础设施的扩展主要由芯片生产的投资驱动。实际上，扩展计算基础设施很困难，因此我们在模型中纳入了物理计算力的陡峭调整成本。这反映了在短时间内生产大量芯片会显着增加边际生产成本的现实。 反过来，硬件和软件效率的提高是由对硬件和软件研发的投资驱动的。这种研发转化为效率提升的程度取决于研发的回报——这反映了研发的可并行化程度，以及想法变得越来越难找到的程度。随着技术限制的临近，这些回报也会随着时间的推移而减少。 硬件研发 增加可用有效计算力的一种方法是制造更好的 AI 芯片。我们认为这些更好的芯片具有更高的硬件效率 H，即每美元每年执行更多的 FLOP。直观地说，更好的芯片使以相同的价格进行更多的计算成为可能。 这些效率提升源于硬件研发投资 IHRD，并且随着想法变得越来越难找到而受到收益递减的影响。这由指数 ϕH 捕获。硬件研发投资的影响也受到参数 λH 的调节，该参数捕获了研发努力相互排挤的程度。总的来说，这些决定了硬件研发的回报 rH=λHϕH，并影响了硬件效率 gH 的增长率。 引入了进一步的参数 θH 来拟合预测的和当前观察到的增长，从而产生以下等式： gH(t)=θH[H(t)]−ϕH[IHRD(t)]λH 硬件研发的回报还受到物理限制的约束。随着硬件效率 H 接近最大值 Hmax，增长率会被 ΛH 定义的因子惩罚，该因子随着 H 的指数增长而线性下降至零。因此，硬件研发的回报最终会降至零。 H˙(t)H(t)=gH(t)ΛH(H(t)) ΛH(H(t))=logHmax−logH(t)logHmax−logH(0)
附加组件：硬件研发楔形
为了解释研发可能带来的积极外部性，GATE 模型包含一个附加组件，允许用户设置“研发楔形”。该楔形反映了硬件研发的私人和社会利益之间的差异，这会影响研发投资水平。当此参数设置为 5 时，研发投资将减少 1/5，以捕获积极外部性降低私人投资回报的效果。 这是根据硬件研发投资 IHRD 对硬件效率 gH 增长率的边际影响来指定的，其中我们将投资除以一个常数“楔形” ξ： ∂gH∂IHRD=θHλH[H(t)]−ϕH(IHRD(t)ξ)λH−1 请注意，这种操作实际上也降低了 社会 投资回报，使其非常保守。但是，我们包含此附加组件是为了考虑积极的外部性对 GATE 模型预测的影响有多大。 软件研发
自动化
在建立了有效计算力储备之后，GATE 模型会分配该储备以促进任务自动化。这通过在训练更好的 AI 系统和运行现有 AI 系统（也称为“推理”）之间分配有效计算力来实现。
随着更多有效计算力投入到训练中，开发越来越强大的 AI 系统成为可能。我们在 GATE 中将其操作化为自动化任务比例的增加。一旦“有效训练计算力”分配变得足够大，自动化任务的比例就会达到 1，这样所有具有经济价值的任务都将实现自动化。
增加“有效推理/运行时计算力”也有助于扩展 AI 系统的能力，例如，因为使用更多的推理计算力可以让模型“推理”更长时间。在每个任务上运行更多的 AI 工作人员也成为可能，从而有助于加深任务自动化。因此，有效的推理计算力既增加了自动化任务的比例，也增加了每个自动化任务的 AI 劳动数量。
为了实现这些动态，我们定义了一个从（推理调整后的）有效训练计算力到可自动化经济价值任务比例的映射，从而捕获了可自动化任务范围如何随着更多有效计算力而增加。然后，我们指定了匹配每个任务的人力工作者需要多少运行时计算力，从而确定了分配给每个任务的“AI 工作者”的总数。
任务自动化扩展
现代 AI 的核心经验见解之一是计算扩展的重要性：开发更强大的 AI 模型的主要方法是通过使用更多有效计算力来训练它们。最重要的是，AI 系统可以通过扩展有效的推理计算力来实现更多——例如，通过运行 AI 系统更长时间来执行更多“推理”。
我们将这些观察结果整合到 GATE 中任务自动化的发生方式中。我们首先将 AI 系统的“能力”操作化为它们能够自动化的经济价值任务 f 的比例。然后，我们将针对推理扩展 CT+ι 调整后的有效训练计算力映射到可自动化任务的比例。
这种推理调整后的有效训练计算力储备的积累始于有效训练计算力 CT 的积累，为简单起见，它在整个模拟过程中都专用于单个连续训练运行。在每个时间步中，新产生的有效训练计算力 D 被添加到总训练计算力储备 CT 中，即：
CT(t)˙=D(t)
虽然 AI 训练纯粹涉及单个连续训练运行显然是不正确的，但这种简化并不会显着影响 GATE 的预测。这是因为大多数训练计算力已经大量集中在大型 AI 实验室的少数训练运行中。此外，训练计算力一直在随着时间的推移呈指数增长——因此对 CT 的贡献主要由新的计算力流主导。
然后，我们使用推理计算因子 ιmax 调整此有效训练计算力储备 CT。此参数定义了可以产生性能改进的最大推理扩展量。将有效推理计算力扩展 m 个数量级对系统性能的影响等同于将 CT 增加一个数量级，因此由此产生的推理调整后的有效训练计算力如下：
CT+ι(t)=CT(t)⋅ιmax1/m
为了将其与任务自动化联系起来，GATE 模型指定了一个从 CT+ι 到可自动化任务 f 的比例的映射。该映射在对数计算中是分段线性的，分为三个部分：（1）低于某个有效计算力阈值时，有效计算力的增加不会转化为自动化任务比例的相应增加。（2）高于此阈值时，自动化线性增加，直到（3）所有任务都实现自动化。如下图所示：
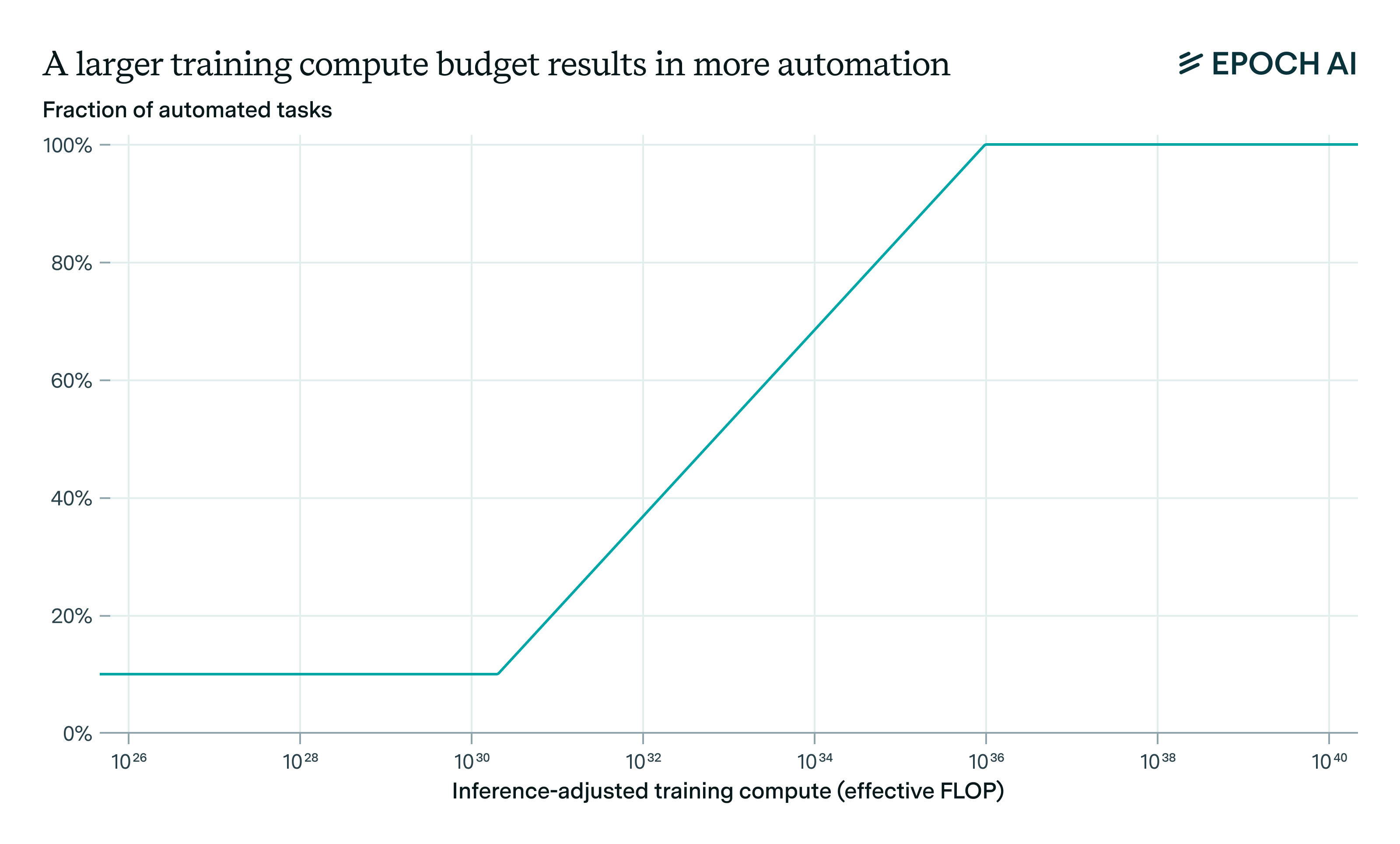该映射隐式地表明，与自动化其他任务相比，需要更多有效训练计算力的任务在根本上更“复杂”。虽然这包括所有具有经济价值的任务，但 GATE 模型并未指定 哪些 任务比其他任务更“复杂”（因此哪些任务将首先实现自动化）。
运行时评估
生产
生产模块捕获了 GATE 的核心宏观经济动态。至关重要的是，它指定了自动化如何映射到全球经济生产，以及如何在模型中做出投资和分配决策。 有效的推理计算力根据其运行时要求分配给不同的自动化任务，从而确定了经济中的“数字 AI 工作者”的数量。AI 工作者和人力工作者共同构成了经济生产的总“有效劳动力”投入。重要的是，非自动化任务上的劳动力投入无法快速扩大，从而对整体生产的快速扩张构成了重大障碍。 然后，有效的劳动力与非 AI 资本和不可累积的生产要素（例如土地或自然资源）相结合，以确定经济的整体产出。由于增长任何单一投入都会带来收益递减，因此当资本和劳动力同步扩张时，生产就会加速。 最后，全球生产（即世界总产值）被分配给消费、传统资本投资或 AI 投资。每个时间步中的消费量被确定为通过梯度下降来帮助最大化代表性家庭的效用函数。 劳动力分配 GATE 允许经济增长潜在大幅加速的主要机制是通过大规模增加劳动力规模。特别是，与人力劳动力相比，计算力的扩展速度要快得多，从而可以大大增加“AI 工作者”的数量和经济产出。 我们根据“有效劳动力” T 来量化劳动力的规模，该有效劳动力是在一系列不同的任务（由索引 i 表示）中求和得出的。不同任务上的劳动力投入 Ti 使用标准的恒定替代弹性 (CES) 函数组合在一起，其中这些任务投入相互补充。 T(t)=(∫01Ti(t)ρdi)1/ρ,whereρ∈(−∞,0). 特别是，强制执行任务之间的互补性意味着我们指定“替代参数” ρ 为负数。这个假设是关键，因为它捕获了著名的“鲍莫尔效应”，即对一项任务的有限投入会扼杀整体产出，并随着时间的推移增加扼杀任务的边际价值。 正如我们在自动化模块中提到的那样，一部分任务 f 已实现自动化，因此可以由人力工作者 Li 或 AI 工作者 Ni 来执行。反过来，AI 工作者是通过将运行时计算力分配给每个任务来创建的，创建 AI 工作者会产生特定于任务的运行时计算成本 Ri。剩余的非自动化任务只能由人类来执行。形式上： Ti(t)={Li(t)+Ni(t),if i≤f(t)Li(t),otherwise 因此，有三种主要途径可以增加有效劳动力的规模：（1）增加人力劳动力的规模，（2）将更多的运行时计算力投入到已自动化的任务中，以及（3）增加自动化任务的比例。与其他半内生增长模型一样，我们假设人力劳动的总量 L 以恒定的指数增长率 gL 增长： L(t)=L(0)egLt 相反，通过途径 (2) 和 (3) 实现的有效劳动力增长是通过自动化来实现的，自动化如上一个模块中所述进行。
附加组件：劳动力分配摩擦
默认情况下，GATE 模型假设可以完美地重新分配人力劳动，工人能够无缝地从自动化任务切换到非自动化任务。但是，有人可能会反对这种假设过于激进，因为在现实中，有许多摩擦会增加人们从自动化任务中切换的时间和成本。 为了解决这个问题，GATE 模型包括一种替代的极端情况：一种 零 人力劳动重新分配成为可能的情况。在这种情况下，劳动力最初在不同的任务之间平均分配，并且随着任务自动化的进行而根本不会转移（尽管我们确实看到每个人力任务 i 中人力劳动力都在不断地呈指数增长）： Li(t)=Li(0)egLt 尽管这两种情况都不现实，但我们将这两个极端视为一种简单评估劳动力重新分配摩擦在模型中的重要性的方法。 经济生产
如何解释 GATE 模型的预测
为了最有效地使用 GATE playground，重要的是了解其预测的解释方式以及模型的局限性。值得注意的是，该模型的预测 并非 旨在代表 Epoch AI 对未来 AI 发展和经济影响的预测。与任何经济模型一样，GATE 模型的预测反而是 有条件的 预测，这取决于一系列假设，包括规格和参数值方面。 特别是，GATE 最适合分析 AI 自动化的宏观定性动态，前提是 AI 能力的改进完全由物理计算的增加和更好的算法驱动。因此，GATE 可用于推导有关 AI 自动化经济影响的程式化事实——相反，其定量预测的可靠性要差得多，不确定性也要大得多。 务必注意，GATE 预测可能会受到优化错误的影响。GATE 是一个复杂的经济模型，具有大量参数，因此由于优化问题，该模型的预测在某些参数范围内变得不可靠。当结果不直观时，尤其重要的是验证模型的预测是否仅仅是由于优化问题造成的。例如，检查这种情况的一种方法是稍微扰乱参数设置，以查看结果是否发生重大变化。如果您发现任何此类错误，请发送电子邮件至 info@epoch.ai。
参数
在本文档中，我们提供了每个参数的简要说明 - 有关更多详细信息（包括各个参数估计的理由），请参阅我们的技术论文。 我们将 GATE 模型的参数分为三类：
- AI 和计算： 与有效计算力的储备以及任务自动化相关的参数
- 技术和研发： 与硬件和软件研发相关的参数
- 一般经济学： 宏观经济模型中常用的参数
此外，我们还概述了核心模型的三大主要附加组件，这些组件考虑了投资者不确定性、劳动力重新分配（或缺乏重新分配）以及研发中的积极外部性。
AI 和计算参数
自动化参数
AGI 训练要求 T 参数 AGI 训练要求 T 说明 训练能够自动化所有任务的 AI 系统所需的有效 FLOP。 单位 eFLOP（数量级） 默认 36.5 理由 我们从 (Cotra, 2020) 中粗略地进行中心估计，该估计使用“生物锚点”（例如，来自人脑或进化）来估计训练变革性 AI 系统的计算要求，从而得出 1e36.5 FLOP。此参数高度不确定，因此我们考虑了几个数量级的不确定性，范围从 1e33 到 1e41，基于 Cotra 报告的 FLOP 要求分布。 FLOP 差距分数 Δf 参数 FLOP 差距分数 Δf 说明 这定义了有效训练计算力（针对推理扩展进行调整）的范围，在此范围内，增加计算力会增加任务自动化。 单位 % 默认 55 理由 这是定义为两个量的比率——第一个量是 log(AGI 训练要求) - log(有效 FLOP 阈值，在该阈值上，更多计算力会导致更多自动化)。这除以第二个量，由 log(AGI 训练要求) - log(初始训练计算力) 给出。因此，这定义为以数量级为单位测量的两个量的比率。形式上，该分数对应于 C(100%)−C(20%)C(100%)−C(init)，其中 C(x%) 是 x% 自动化所需的计算力的以 10 为底的对数。直观地说，此参数捕获了 AGI 之前的系统何时开始自动化经济。如果此参数为零，则只有 AGI 可以自动化任何内容；如果此参数为 1，那么我们在当前训练运行规模下会看到自动化的稳定线性进展。由于我们只有关于此参数的微弱证据，因此我们对它的值采用相当广泛的分布。一些研究表明，当今的 AI 系统已经可以自动化一些旧系统无法自动化的任务 (Owen and Besiroglu, 2023)，其他来源预测未来十年存在自动化 (Davidson, 2023) 或暴露 (Eloundou et al., 2023) 的潜力。根据当前趋势，十年涉及 5 个数量级的计算扩展 (Epoch AI, 2023)，即 1e30.5 FLOP。作为我们中值训练要求的 FLOP 差距分数，这会导致大约 0.55 的 FLOP 差距分数。对于我们范围的下限，我们注意到一些 AI 研究人员预计，在相对较小的计算扩展范围内，AI 能力将得到快速改进。如果我们假设 ~2 个数量级的计算力可以将 AI 系统从无关紧要的状态提高到自动化经济的一半，那么这大致对应于 Δf≈2∗2/11=0.4，适用于我们的 AGI 训练要求 T 范围。对于我们的上限，我们考虑需要 2 个数量级才能达到自动化任务比例增加的情况，这会导致分数为 Δf=(11−2)/11≈0.8。 参数 | 说明 | 单位 | 默认值 | 理由 ---|---|---|---|--- AGI 训练要求 T | 训练能够自动化所有任务的 AI 系统所需的有效 FLOP。 | eFLOP（数量级） | 36.5 | 我们从 (Cotra, 2020) 中粗略地进行中心估计，该估计使用“生物锚点”（例如，来自人脑或进化）来估计训练变革性 AI 系统的计算要求，从而得出 1e36.5 FLOP。此参数高度不确定，因此我们考虑了几个数量级的不确定性，范围从 1e33 到 1e41，基于 Cotra 报告的 FLOP 要求分布。 FLOP 差距分数 Δf | 这定义了有效训练计算力（针对推理扩展进行调整）的范围，在此范围内，增加计算力会增加任务自动化。 | % | 55 | 这是定义为两个量的比率——第一个量是 log(AGI 训练要求) - log(有效 FLOP 阈值，在该阈值上，更多计算力会导致更多自动化)。这除以第二个量，由 log(AGI 训练要求) - log(初始训练计算力) 给出。因此，这定义为以数量级为单位测量的两个量的比率。形式上，该分数对应于 C(100%)−C(20%)C(100%)−C(init)，其中 C(x%) 是 x% 自动化所需的计算力的以 10 为底的对数。直观地说，此参数捕获了 AGI 之前的系统何时开始自动化经济。如果此参数为零，则只有 AGI 可以自动化任何内容；如果此参数为 1，那么我们在当前训练运行规模下会看到自动化的稳定线性进展。由于我们只有关于此参数的微弱证据，因此我们对它的值采用相当广泛的分布。一些研究表明，当今的 AI 系统已经可以自动化一些旧系统无法自动化的任务 (Owen and Besiroglu, 2023)，其他来源预测未来十年存在自动化 (Davidson, 2023) 或暴露 (Eloundou et al., 2023) 的潜力。根据当前趋势，十年涉及 5 个数量级的计算扩展 (Epoch AI, 2023)，即 1e30.5 FLOP。作为我们中值训练要求的 FLOP 差距分数，这会导致大约 0.55 的 FLOP 差距分数。对于我们范围的下限，我们注意到一些 AI 研究人员预计，在相对较小的计算扩展范围内，AI 能力将得到快速改进。如果我们假设 ~2 个数量级的计算力可以将 AI 系统从无关紧要的状态提高到自动化经济的一半，那么这大致对应于 Δf≈2∗2/11=0.4，适用于我们的 AGI 训练要求 T 范围。对于我们的上限，我们考虑需要 2 个数量级才能达到自动化任务比例增加的情况，这会导致分数为 Δf=(11−2)/11≈0.8。
运行时计算参数
最大推理-训练计算权衡 ιmax 参数 最大推理-训练计算权衡 ιmax 说明 推理乘数的最大值。这包括来自减少过度训练和增加推理扩展的效果，这两者都会增加乘数（其中“未调整的运行时计算成本”假设最大过度训练）。 单位 数量级 默认 5 理由 (Villalobos and Atkinson, 2023) 认为，可以增加 2-6 个数量级的推理来换取训练计算力，具体取决于任务类型。因此，对于我们的中心估计，我们选择 4 个数量级。 推理-训练权衡斜率 m 参数 推理-训练权衡斜率 m 说明 推理计算权衡在确定系统有效计算力大小时的斜率。这捕获了在实现相同性能水平的同时，可以用多少个数量级的推理计算力来替代 1 个数量级的训练计算力。 单位 无量纲 默认 2 理由 我们基于 (Villalobos and Atkinson, 2023) 的估计将我们的中心估计设置为 2 个数量级，并允许大约 2 倍的不确定性，这与提供的估计大致一致。 最小运行时计算要求 10γ0 参数 最小运行时计算要求 10γ0 说明 在最大过度训练的情况下（即，在最大限度地增加训练计算力以最大限度地减少未来推理成本之后），替代最容易自动化的任务的工作人员的最小运行时计算成本。 单位 eFLOP/年（数量级） 默认 15 理由 对于此参数，我们松散地锚定到 OCR（即光学字符识别）等最早的自动化任务之一所需的推理计算力。每个正向传递需要数十万到一百万次乘加运算，因此我们松散地锚定到每个正向传递大约 1M FLOP（例如，LeNet-4 涉及每个正向传递 26 万次乘加运算 (Bottou et al., 1994))。假设每个正向传递可用于分析一个字符，并且每秒处理大约