聊聊 Superhyperbola(超双曲线)
文章介绍了**Superhyperbola(超双曲线)**的概念,它类似于**Superellipse(超椭圆)**,是双曲线的推广。文章给出了**Superhyperbola**的数学方程,并探讨了参数 _p_ 对其形状的影响。当 _p_ 增加时,**Superhyperbola**在顶点处会变得更加钝化。文章还讨论了**Superhyperbola**不如**Superellipse**常见的原因,并分析了命名和推广方面的问题。
Superhyperbola(超双曲线)
发布于 2025年3月27日,作者:John
椭圆的方程是:
双曲线的方程是:
类似地,**Superellipse(超椭圆)**的方程是:
那么,**Superhyperbola(超双曲线)**的方程就是:
当 p = 2 时,绝对值符号是不必要的,Superellipse 和 Superhyperbola 就分别简化为椭圆和双曲线。
增加 p 的值会使 Superellipse 更像一个矩形。但与带有圆角的矩形不同,Superellipse 的曲率变化是连续的。
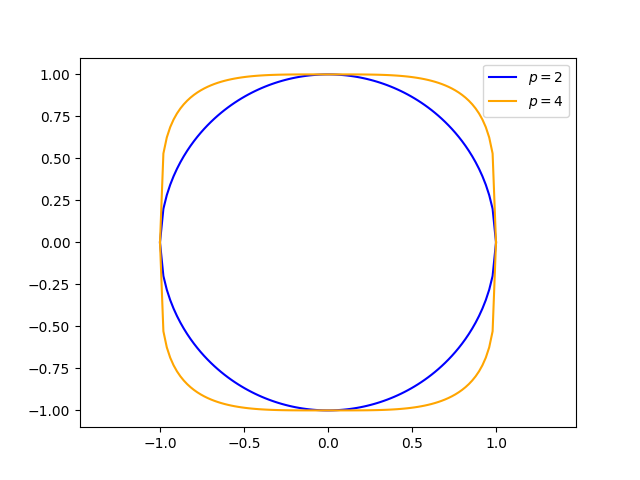
增加 p 的值会使 Superhyperbola 在顶点处更加钝化。
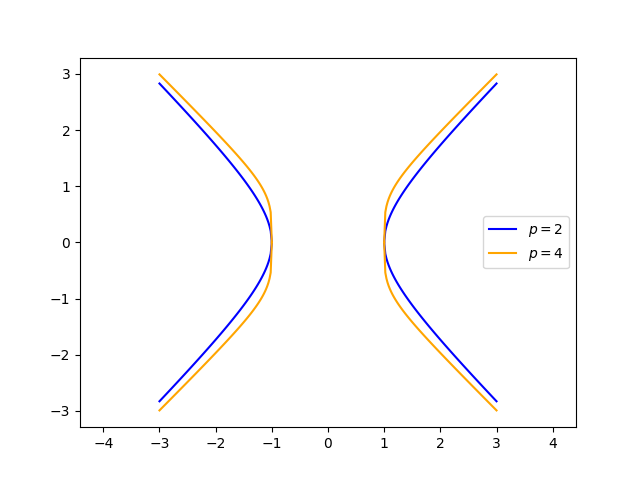
市场推广角度
Superellipse 是椭圆的一个相当常见的变体。即使你不熟悉这个术语,你也可能见过这种形状。我在这里给出了几个例子。 Superhyperbola 是 Superellipse 显而易见的类似物,但这个术语远没有那么常见。 我昨天才第一次听到这个词。
目前还不清楚为什么 Superellipse 很常见,而 Superhyperbola 却如此默默无闻,以下是一些推测。 首先,Superellipse 有一个倡导者,Piet Hein。 如果 Superhyperbola 也有倡导者,那他并不是一个非常有力的倡导者。
这个名字也很令人反感:将 super 和 hyper 并列听起来很傻。 词源很有意义,即使听起来很滑稽。 Piet Hein 使用前缀 super - 指的是将指数从通常的值 2 增加。 不幸的是,hyperbola 以一个类似于 super 的词根开头。