过度设计的 Anchor Links 实现
网站导航
公司
合作伙伴
案例
人员
- Bob Wassermann
- Driek van der Meulen
- Frank Slangen
- Juul Crooymans
- Mats Erdkamp
- Nielson Office dog
- Pascal van der Steen
- Roel Janssen
- Sem Stassen
- Tristan Vranken
文章
联系
关闭
页面
关闭
 SLSQP
SLSQP (Sequential Least Squares Programming) 是一种优化算法,用于解决约束非线性问题。它通过迭代改进解决方案,同时满足等式和不等式约束来工作。 在每个步骤中,它使用更简单的二次模型和线性约束来近似问题,使其对于具有平滑梯度的问题有效。当目标和约束都可微时,SLSQP 通常用于工程、机器学习和运筹学。
SLSQP
SLSQP (Sequential Least Squares Programming) 是一种优化算法,用于解决约束非线性问题。它通过迭代改进解决方案,同时满足等式和不等式约束来工作。 在每个步骤中,它使用更简单的二次模型和线性约束来近似问题,使其对于具有平滑梯度的问题有效。当目标和约束都可微时,SLSQP 通常用于工程、机器学习和运筹学。
 Hotfix: 额外填充
Practical: 移动触发线
Good: 平移触发点
Great: 分数平移触发点
Awesome: 创建自定义映射函数
验证
Hotfix: 额外填充
Practical: 移动触发线
Good: 平移触发点
Great: 分数平移触发点
Awesome: 创建自定义映射函数
验证
Overengineered anchor links
Overengineeredanchorlinks
![]() Mats Erdkamp 于 2025 年 3 月 21 日
Mats Erdkamp 于 2025 年 3 月 21 日
Anchor links 起初看起来非常简单:点击一个按钮,滚动到标题,完成。但是,如果你曾经必须实现它们,你可能遇到过“active anchor problem”。问题在于,页面底部的标题可能太靠下,无法滚动到所需的位置。上面的示例组件显示了“conclusion”标题永远无法到达的情况。这肯定会对用户体验产生不利影响。我们需要想出一个解决方案。在这篇博文中,我将展示我想出的一些解决方案——从一个 hotfix 到完全失控。但在我们这样做之前,让我们创建一个更抽象的可视化。在这里,我们看到一个视口向下移动页面,触发线设置为视口顶部以下 25vh 的位置。这就是我们将用来可视化不同解决方案的内容。
Hotfix: 额外填充
最简单的解决方案是添加额外的填充。我们通过取最后一个标题和 anchor 触发器可以到达的最低点之间的 delta 来计算填充的高度。完美,对吧?好吧,有时设计团队不太喜欢随机的额外填充,所以让我们继续搜索。
Practical: 移动触发线
也许可以移动触发线,而不是添加额外的填充。这也非常容易做到,我们只需要计算最后一个标题距离底部有多远,并将触发线也放在那里。但是,这将意味着当用户点击 anchor 标签时,标题可能会一直放在视口的底部。这当然不好,因为大多数人将他们阅读的文本放在屏幕的上半部分。我们需要继续寻找。
Good: 平移触发点
我们可以向上平移标题,而不是移动触发线。我们不是使用标题的实际位置作为触发器的原因,而是创建虚拟标题并将它们向上平移。虚拟标题实际上在文章中不可见,它只是我们用来指示活动状态的位置。有人可能会争辩说,这在概念上与移动触发线几乎相同,他们是对的。但是,考虑平移触发点给了我们更多的心理灵活性,因为它允许我们考虑根据每个标题的位置应用_不同_的调整,这在以后至关重要。
示例可视化现在显示了这些“虚拟标题”的位置。因此,虽然标题在文章中的位置相同,但我们可视化了它的触发点的位置。
在示例中,我们看到一个问题出现:第一个标题现在太高了。这种新方法的好处是我们可以非常优雅地解决这个问题,因为我们可以轻松地移动各个虚拟标题。但这样做的好方法是什么呢?
Great: 分数平移触发点
如果我们考虑一下,我们不需要平移所有触发点。只需要满足几个条件:
- 标题需要可到达。
- 标题需要保持顺序。
我们可以通过分数平移触发点来满足这些条件。在这里,第一个标题不移动,最后一个标题向上移动到完全可到达所需的全部量。其他标题根据它们在第一个和最后一个标题之间的位置按比例向上移动。现在我们正在取得进展!这是一个可靠的解决方案。你可能想在这里停下来,以免你的产品经理开始给你困惑的眼神,想知道“修复 anchor links”怎么突然变成了一个为期三周的 epic。
Awesome: 创建自定义映射函数
虽然分数解决方案有效,因为我们的条件得到了满足,但它确实存在一些缺陷。我们选择了一条触发线,它从视口顶部向下 25%。如果我们实际上可以最小化所有标题与此理想线之间的偏差,那就太好了。触发器越接近这条(请记住——半任意选择的)线,用户体验_应该_越好。最小化偏差感觉像是一个好的启发式方法。这肯定会让用户更快乐,并导致股东价值增加。
让我们最小化标题的原始位置和虚拟位置之间的 delta 的均方误差 (MSE)。我们使用 MSE 是因为它会严重惩罚较大的偏差,从而推动系统进入一种状态,其中大多数虚拟标题都接近其原始位置,同时仍然满足我们的可达性约束。当然,标题必须保持顺序的约束仍然适用。这导致所有可到达的点都停留在其原始位置。看起来我们有问题。标题聚集在底部。这是有道理的,因为最小化均方误差只关心接近原始位置;它没有阻止这种聚集的“力”。我们需要定义一些鼓励虚拟触发点保持一定距离的东西,理想情况下与它们原来的间距相关。考虑到用户体验,我们可能会假设,激活下一节的 anchor 所需的滚动_距离_与该节的实际内容长度成比例是很好的。这种“各节想要保持其相对滚动长度”的力就是我们将要使用的。
Side quest: 最小化函数
为了探索这个想法,我们需要爆发出… Python。在这里,我们(阅读:Claude 和我)实现了一个 SLSQP SLSQP (Sequential Least Squares Programming) 是一种优化算法,用于解决约束非线性问题。它通过迭代改进解决方案,同时满足等式和不等式约束来工作。 在每个步骤中,它使用更简单的二次模型和线性约束来近似问题,使其对于具有平滑梯度的问题有效。当目标和约束都可微时,SLSQP 通常用于工程、机器学习和运筹学。 SLSQP 求解器,它是一种数值优化算法,专为像我们这样的约束问题而设计。优化的核心在于一个具有两个竞争项的损失函数:
- Anchor penalty: 虚拟标题从其原始位置移动了多远。 最小化这一点可使虚拟标题接近其原始位置。 (Lanchor=∑(yvirtual−yoriginal)2L_{anchor} = \sum (y_{virtual} - y_{original})^2Lanchor=∑(yvirtual−yoriginal)2)
- Section penalty: 每个虚拟部分(两个虚拟标题之间的空间)的大小与原始部分的大小差异有多大。 最小化这一点可确保各部分在滚动距离方面不会变得过短或过长。 (Lsection=∑((yi+1,virtual−yi,virtual)−(yi+1,original−yi,original))2L_{section} = \sum ((y_{i+1, virtual} - y_{i, virtual}) - (y_{i+1, original} - y_{i, original}))^2Lsection=∑((yi+1,virtual−yi,virtual)−(yi+1,original−yi,original))2)
我们将它们组合成总损失 L=wanchorLanchor+wsectionLsectionL = w_{anchor} L_{anchor} + w_{section} L_{section}L=wanchorLanchor+wsectionLsection,其中权重 wanchorw_{anchor}wanchor 和 wsectionw_{section}wsection 控制折衷 (wanchor+wsection=1w_{anchor} + w_{section} = 1wanchor+wsection=1)。
我们定义约束来:
- 将虚拟标题保持在页面边界内。
- 确保第一个标题不会向上浮动(其虚拟位置必须 >= 其原始位置)。
- 保持虚拟标题的顺序 (yi+1,virtual≥yi,virtualy_{i+1, virtual} \ge y_{i, virtual}yi+1,virtual≥yi,virtual)。
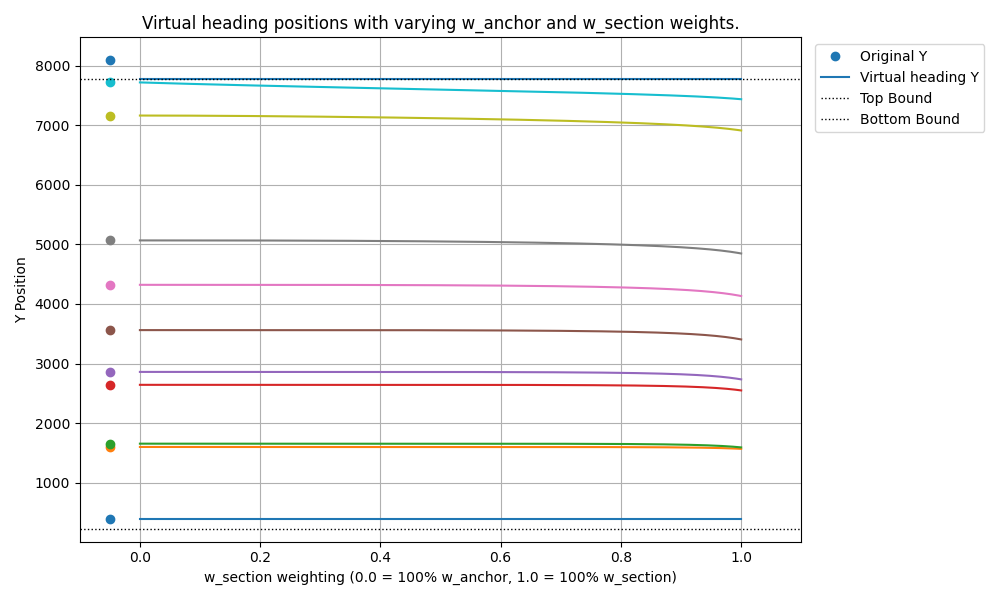
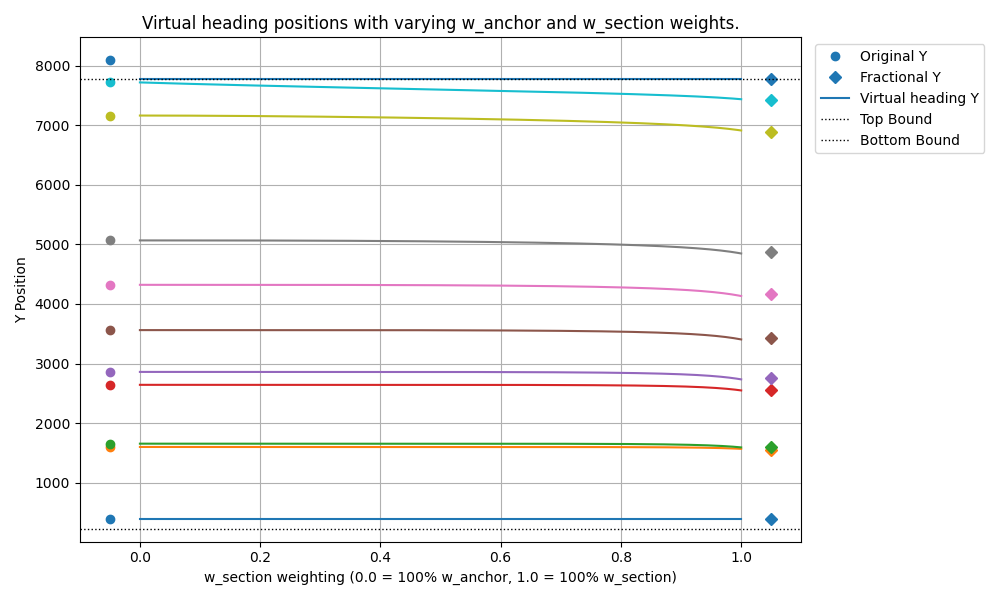
由此,我们生成一个图,显示虚拟标题的位置如何随着我们改变权重而变化(具体而言,当 wsectionw_{section}wsection 从 0 增加到 1 时)。
运行该代码会给我们
 这个图。左侧(在 wsection=0w_{section} = 0wsection=0)的圆圈代表原始标题位置。这些线显示了每个虚拟标题的位置(Y 轴)如何随着部分 penalty 权重 wsectionw_{section}wsection(X 轴)的增加而变化。在左侧,首要任务是使标题靠近其原始位置(高 wanchorw_{anchor}wanchor)。在右侧,首要任务转移到保留标题之间的原始间距(高 wsectionw_{section}wsection)。我很好奇看看这与我们之前尝试过的简单分数平移相比如何。并且难道
这个图。左侧(在 wsection=0w_{section} = 0wsection=0)的圆圈代表原始标题位置。这些线显示了每个虚拟标题的位置(Y 轴)如何随着部分 penalty 权重 wsectionw_{section}wsection(X 轴)的增加而变化。在左侧,首要任务是使标题靠近其原始位置(高 wanchorw_{anchor}wanchor)。在右侧,首要任务转移到保留标题之间的原始间距(高 wsectionw_{section}wsection)。我很好奇看看这与我们之前尝试过的简单分数平移相比如何。并且难道
 你不知道吗,当部分 penalty 占主导地位时(wsection=1w_{section} = 1wsection=1)!分数平移正是优化器所确定的!
你不知道吗,当部分 penalty 占主导地位时(wsection=1w_{section} = 1wsection=1)!分数平移正是优化器所确定的!
实现
盯着优化图引发了一个想法。好吧,也许是两个想法。首先,需要保留部分间距,这真的会在页面_末尾_开始起作用,标题会被强制向上推以保持可达性,从而将最后的部分挤压在一起。其次,让我们考虑一下“分数平移”方法在边缘情况下的行为。
想象一下,如果你愿意,将整本圣经,从创世纪的“起初”到启示录的最后一个“阿门”,渲染为一个连续的可滚动网页。(对于我们中的技术兄弟:你也可以想象将 Paul Graham 的所有文章背靠背地粘在一起)。现在,假设最后一个标题,也许是“启示录第 22 章”,当滚动到时,仅比我们的触发线低 200 像素。
我们之前的“分数平移”在这里有意义吗?这意味着获取所需的 200 像素的提升,并仔细地将该调整分布到_每个标题_,一直到开始。十诫得到了一个小小的提升,诗篇略多一些,所有这些都最终使启示录 22 得到完整的 200 像素提升。
实际上,如果你考虑一下,对于分数平移,误差(虚拟标题和原始标题之间的距离)会随着页面长度的增加而增加。因此,如果页面趋于无穷大,误差也会趋于无穷大!这当然很草率,并且用户可能会立即注意到感觉不对劲。那么我们将如何解决这个问题呢?
最终版本
这导致了我们对更智能的映射函数的期望行为:
- 对于靠近页面末尾的标题,应用更多调整(表现得像高 wsectionw_{section}wsection)。
- 对于靠近页面开头的标题,应用更少的调整(或理想情况下不应用调整)(表现得像高 wanchorw_{anchor}wanchor)。
- 这些状态之间的过渡应该平滑。
我们需要一个函数,该函数将标题的标准化位置 x∈[0,1]x \in [0, 1]x∈[0,1](其中 x=0x=0x=0 是第一个标题,x=1x=1x=1 是最后一个)映射到“调整因子” y∈[0,1]y \in [0, 1]y∈[0,1]。此因子确定将最大所需提升的_多少_应用于位置 xxx 处的标题。
我们需要这个映射函数 y=f(x)y = f(x)y=f(x) 具有特定的属性:
- 它必须从零开始:f(0)=0f(0) = 0f(0)=0。
- 它必须以一结束:f(1)=1f(1) = 1f(1)=1。
- 过渡应该平缓地开始:f′(0)=0f'(0) = 0f′(0)=0。
- 过渡应该平缓地结束:f′(1)=0f'(1) = 0f′(1)=0。
事实证明,我们可以从计算机图形领域借用一个函数来解决这个问题。 smoothstep 函数是一个三次多项式,它在 x∈[0,1]x \in [0, 1]x∈[0,1] 范围内从 0 平滑过渡到 1。
S(x)=3x2−2x3S(x) = 3x^2 - 2x^3S(x)=3x2−2x3
此函数在整个范围 x∈[0,1]x \in [0, 1]x∈[0,1] 上提供平滑过渡。但是,如果我们不希望过渡立即开始怎么办?如果我们希望调整因子 yyy 在 xxx 达到某个点(比如说 aaa)之前保持为 0,然后在 xxx 到达 1 之前平滑过渡到 1 怎么办?
我们可以通过在将输入 xxx 馈入 smoothstep 函数之前对其进行预处理来实现这一点。让我们定义一个中间变量 ttt,它表示过渡阶段_内_的进度,该阶段发生在 x=ax=ax=a 和 x=1x=1x=1 之间。我们希望 ttt 从 0 到 1,而 xxx 从 aaa 到 1。此线性映射的公式为:
traw=x−a1−at_{raw} = \frac{x - a}{1 - a}traw=1−ax−a
现在,我们需要处理 xxx 在 [a,1][a, 1][a,1] 范围之外的情况。
- 如果 x<ax < ax<a,则 trawt_{raw}traw 为负数。 在这种情况下,我们希望 ttt 为 0。
- 如果 x>1x > 1x>1,则 trawt_{raw}traw 大于 1。 在这种情况下,我们希望 ttt 为 1。(尽管 xxx 定义在 [0,1][0,1][0,1] 上,但 clamping 确保了鲁棒性)。
我们可以使用 min 和 max 函数来实现此 clamping:
t=min(max(traw,0),1)t = \min(\max(t_{raw}, 0), 1)t=min(max(traw,0),1) t=min(max(x−a1−a,0),1)t = \min\left(\max\left(\frac{x - a}{1 - a}, 0\right), 1\right)t=min(max(1−ax−a,0),1)
此 ttt 值现在完全按照我们的需要运行:对于 x≤ax \le ax≤a,它为 0,对于 a≤x≤1a \le x \le 1a≤x≤1,它从 0 线性增加到 1,对于 x≥1x \ge 1x≥1,它为 1。
最后,我们将 smoothstep 函数应用于此 clamped 和 scaled 输入 ttt,以获得我们的最终调整因子 yyy:
y=S(t)=3t2−2t3y = S(t) = 3t^2 - 2t^3y=S(t)=3t2−2t3
这允许我们使用参数 aaa(其中 0≤a<10 \le a < 10≤a<1)来控制平滑向上调整标题开始的标准化位置。设置 a=0a=0a=0 会在整个范围内给出原始 smoothstep,而设置 a=0.5a=0.5a=0.5(例如)意味着页面前半部分的标题根本不会移动,并且调整仅在后半部分平滑上升,从而有效地 localized 更改。
让我们选择 a=0.4a=0.4a=0.4,看看这个调整后的 smoothstep 会做什么。(如果你好奇我是如何找到 0.4 的,那可能会成为第 2 部分的主题……这可能涉及也可能不涉及盲人 ELO 排名。对于更新,最好在这里关注我 here.)
它…很美。
验证
所以,我们终于完成了。我们为了修复 anchor links 已经走到了前所未有的深度。一项真正 Carmack 式的壮举,将被后代铭记。让我们问问首席设计师,
 他的想法。
他的想法。
…哦,好吧,至少我们从中得到了一篇博文。
想要为你的项目设计过度的 anchor links 吗?联系我们!