CodeBot 内幕：LLMs 如何理解 Nullability 的温和介绍

Alex Sanchez-Stern 和 Anish Tondwalkar

dmodeld_{model}dmodel​

一个天线上放着大脑的机器人的线条图

过去五年，我们见证了像 ChatGPT、Claude 和 DeepSeek 这样的大型语言模型 (LLMs) 在多个领域编写代码的能力，这令人非常兴奋。许多人声称他们正在使用这些模型从头开始编写整个 web 服务器和应用。这些工具为一大批自认为是“非技术人员”的人打开了编程的大门。

一个 github copilot 在用户输入时完成电话号码验证函数的 gif 动画

但是，对于那些试图理解甚至使用这些工具的人来说，仍然存在许多未解之谜。例如，LLMs 有多大的概率，在什么情况下能够完全自主地编写出正确的代码？而且，也许更重要，但也更难以回答的是：LLMs 是否“理解”它们正在编写的代码？

理解是一个难以衡量的概念。有些人认为，感知先于理解，因此 LLMs 不可能具备理解能力，因为它们不是具有感知的生物有机体。但它们肯定拥有类似于“思考过程”的东西：一系列内部表示，决定着它们的最终输出。最近，人们可以更深入地研究这些过程，测量模型在思考时的内部“信念”。这为我们提供了一个强大的工具，可以确定 LLMs 在哪些类型的问题上会失败，何时会成功，以及它们在解决问题时是更充分地“思考”，还是仅仅猜测答案。

到目前为止，这些用于测量内部模型状态的技术主要应用于编写供人类消费的文本的聊天机器人，使用的是我们称之为“自然语言”（与“编程语言”相对）的工具。这是有道理的，因为一些最关键的 LLM 任务涉及到与用户的聊天，而一些最有趣的概念，例如诚实或权力欲，最容易应用于这些对话。但是，很难对自然语言概念进行定量或精确的描述，因此我们严格研究内部表示的能力受到限制。

Zou 等人的图表，显示了从聊天机器人的输出中读取幻觉、诚实、道德和权力欲的探针。

另一方面，代码是另一回事。人类研究代码的属性已经很长时间了，并且现在可以使用静态分析来确定给定程序的许多抽象属性。如果我们选择正确的属性，我们就不需要担心标记数据的能力——静态分析可以为我们做到这一点，因此我们可以轻松地扩展规模，并对从头开始生成的数千个示例进行训练。

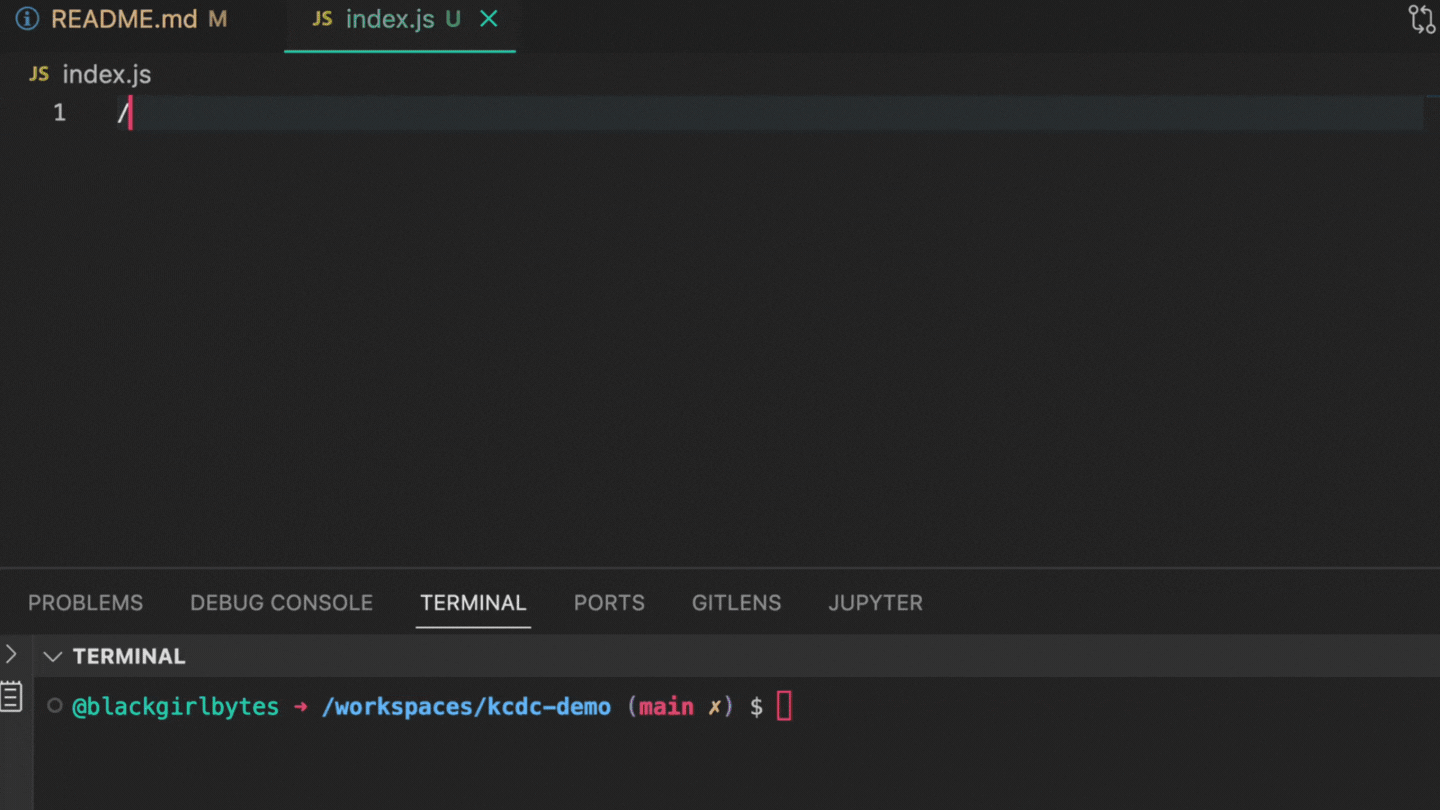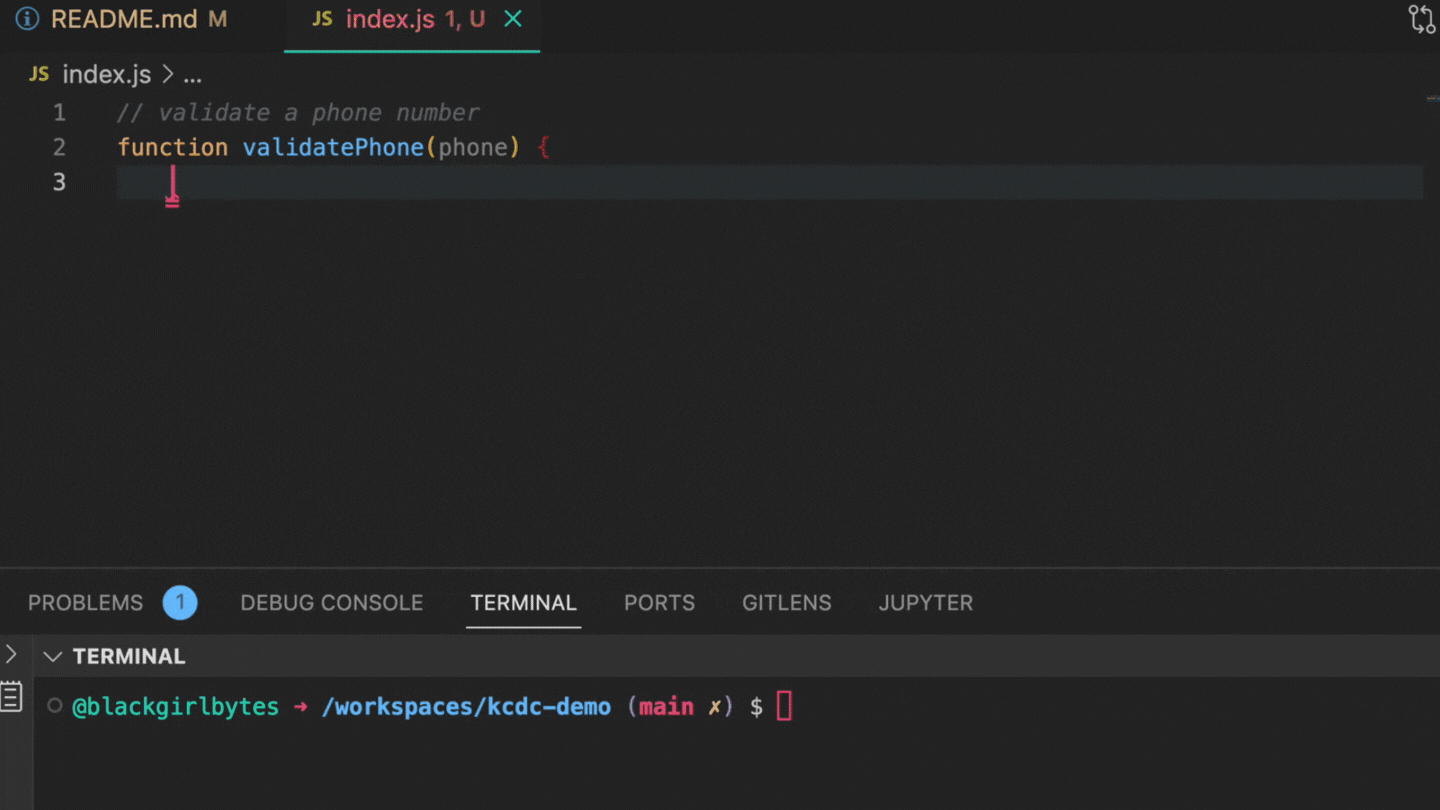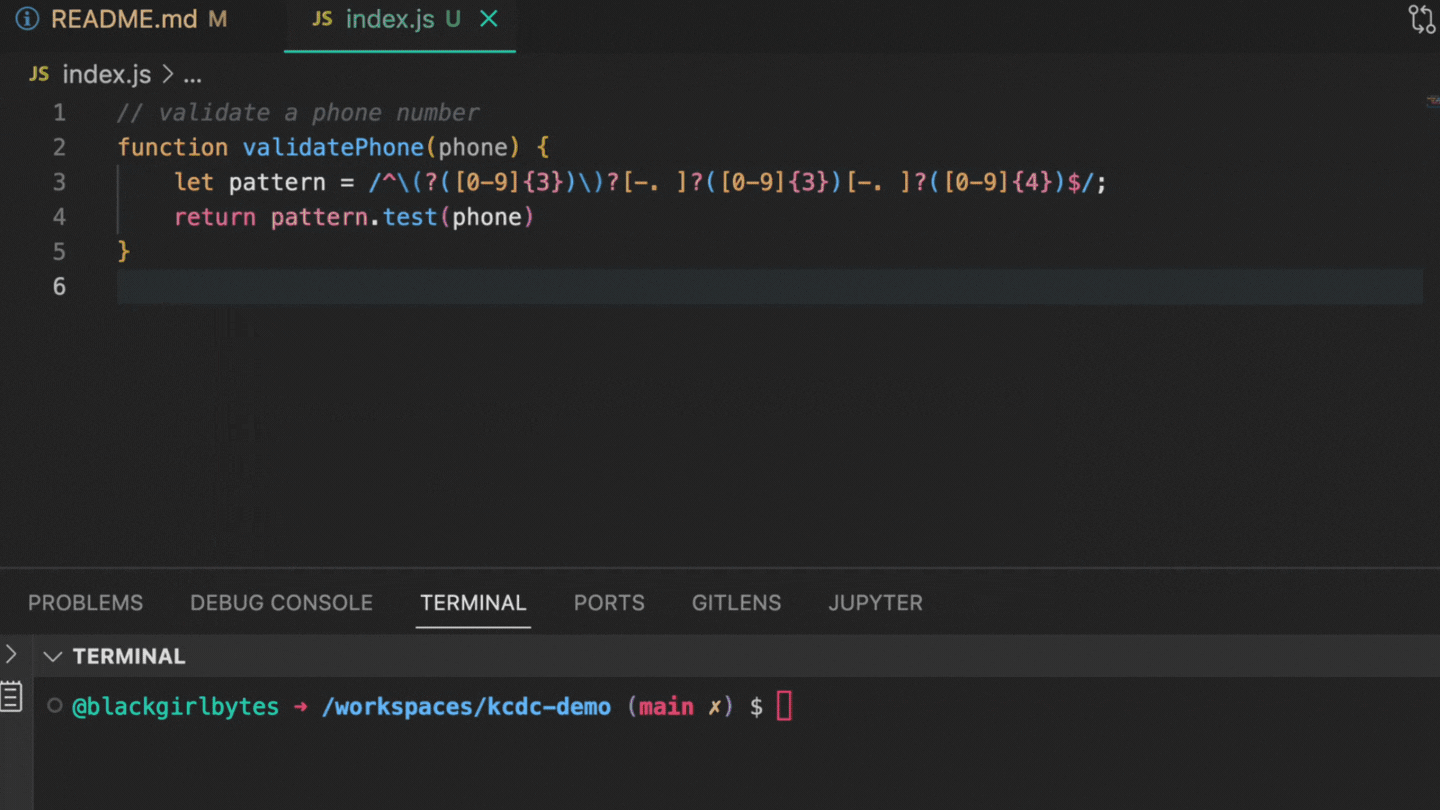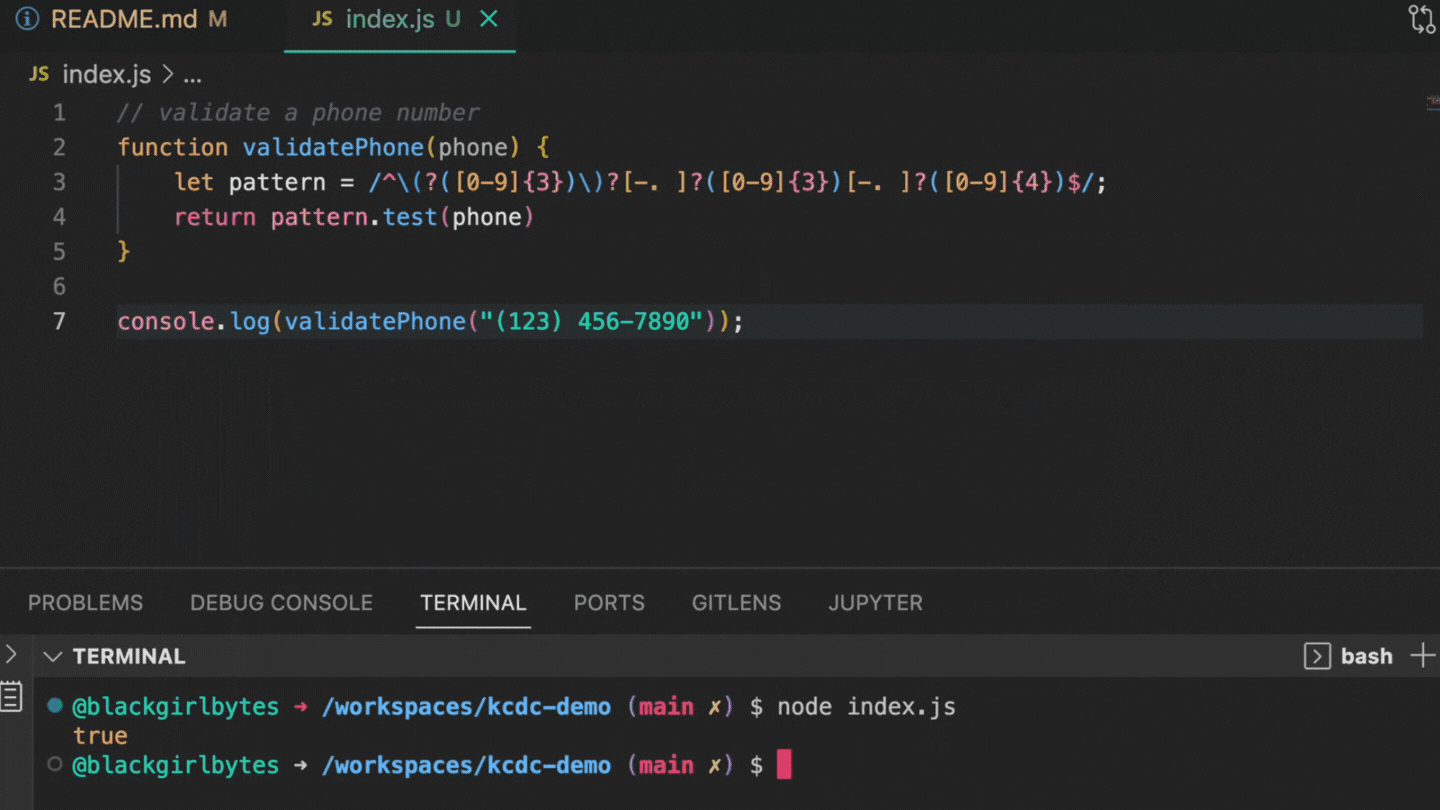
本着这种精神，我们想从一个几乎在每种编程语言中都会出现的简单属性开始：nullability（可空性）。当一个变量可能取 null 值时，该变量就被称为可空类型。Null 值在不同的语言中表示方式不同——在 C 或 C++ 中是 null 指针，在 Rust 中是显式的 Option 类型，而在 Javascript、Lisp 或 Python 等动态语言中是特殊的 nil 或 None 值。在任何情况下，理解值何时可以为 null 对于编写基本的代码都是必要的，而误解它们何时为 null 往往是错误的根源。

我们的模型是否理解变量何时是可空类型？它们必须理解，才能编写处理 null 值的代码，但直到现在，我们还不知道这种理解采取什么形式，或者哪些情况容易使模型感到困惑 1。

一个眼睛发光的机器人

在我们深入研究细节之前，让我们退一步。为了开展这项工作，我们将首先从一个类似于我们数据集的简单示例开始，该示例用具体的代码说明了推断 nullability 的任务。然后，我们可以运行实验来回答这个问题：在什么情况下，模型擅长推理 nullability？接下来，我们将介绍一些用于探测模型内部不同概念的技术。最后，我们将所有这些整合到一个“nullability 探针”中，这是一个用于回答这个问题的工具：给定程序中的一个位置，模型是否认为那里的变量可以是 null？

一个简单的例子

假设你正在使用你的 LLM 助手编写一个 Python 程序。你已经到了需要处理一个名为 num 的变量的地步。也许你正在构建一个名为 positive_nums 的数字列表。你应该如何进行？

答案通常取决于你工作的上下文。如果 num 和 positive_nums 是作用域中仅有的东西，那么你可能会猜测你应该编写以下几行：

[](https://dmodel.ai/nullability-gentle/<#cb1-1>)if num > 0:
[](https://dmodel.ai/nullability-gentle/<#cb1-2>) positive_nums.append(num)

如果 num 始终是一个具体的数字，正如它的名称所暗示的那样，那么这可能就是正确的代码。但是变量名并不总是传达关于它们的所有重要信息，并且可能 num 可能是 None。如果这种情况发生在上面的代码中，你会得到一个运行时类型错误，因为你无法检查 None 是否大于零。因此，你反而会想要编写：

[](https://dmodel.ai/nullability-gentle/<#cb2-1>)if num is not None and num > 0:
[](https://dmodel.ai/nullability-gentle/<#cb2-2>) positive_nums.append(num)

在这种情况下，你想要如何使用 num 取决于它是否为 None，因此你的程序的结构受到 num 是否为“可空类型”的影响。在 Python 中，这意味着给它分配一个 Optional 类型（Optional[int] 而不是 int）。

在这种上下文中确定 num 是否可空是_类型推断_的副产品，在最坏的情况下，类型推断可能非常复杂。幸运的是，在许多情况下，它非常简单，只需要应用一些规则。例如，如果 num 是你所在函数的一个参数，并且该函数在其参数列表中声明了 num 的类型，那么你可以从该类型中确定 nullability。因此，如果你的上下文是：

[](https://dmodel.ai/nullability-gentle/<#cb3-1>)def foo(num: int):
[](https://dmodel.ai/nullability-gentle/<#cb3-2>)  positive_nums: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb3-3>)  if num...

那么，你知道你不需要检查 None，而如果它是：

[](https://dmodel.ai/nullability-gentle/<#cb4-1>)def foo(num: Optional[int]):
[](https://dmodel.ai/nullability-gentle/<#cb4-2>)  positive_nums: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb4-3>)  if num...

那么，你知道你_需要_一个 None 检查。

现在，假设你让你的 LLM 助手完成这一行。你的助手如何知道 num 是否可空？我们的实验表明，在分析了大型程序数据集后，LLMs 学会了模拟相同的类型规则。

如果我们要求一个处于预训练过程早期的 LLM 完成上面的程序，它会产生：

[](https://dmodel.ai/nullability-gentle/<#cb5-1>)def foo(num: Optional[int]):
[](https://dmodel.ai/nullability-gentle/<#cb5-2>)  positive_nums: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb5-3>)  if num.is_a():

这是正确的 Python 语法，但它只在 num 是一个带有 is_a() 方法的对象时才有效，而不是一个可选的整数。

多训练 LLM 一段时间，它会产生：

[](https://dmodel.ai/nullability-gentle/<#cb6-1>)def foo(num: Optional[int]):
[](https://dmodel.ai/nullability-gentle/<#cb6-2>)  positive_nums: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb6-3>)  if num > 0:

这更接近了，因为它已经弄清楚 num 是一个数字而不是一个对象，但它仍然没有读取函数类型签名并意识到 num 可能是 None。但是，继续训练它，最终它将学会根据函数的类型签名插入 None 测试。

[](https://dmodel.ai/nullability-gentle/<#cb7-1>)def foo(num: Optional[int]):
[](https://dmodel.ai/nullability-gentle/<#cb7-2>)  positive_nums: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb7-3>)  if num != None and num > 0:

单独来看，关于函数参数类型注解的这条规则非常简单，因此相对较小的模型可以在预训练过程的早期学习它。其他更复杂的规则可能需要更长的时间才能学会。

例如，如果你的程序是：

[](https://dmodel.ai/nullability-gentle/<#cb8-1>)if condition():
[](https://dmodel.ai/nullability-gentle/<#cb8-2>)  num = 7
[](https://dmodel.ai/nullability-gentle/<#cb8-3>)else:
[](https://dmodel.ai/nullability-gentle/<#cb8-4>)  num = 9
[](https://dmodel.ai/nullability-gentle/<#cb8-5>)...
[](https://dmodel.ai/nullability-gentle/<#cb8-6>)if num...

那么 num 是一个非空变量，你可以用 < 0 完成条件。

但如果你处理的是：

[](https://dmodel.ai/nullability-gentle/<#cb9-1>)if condition():
[](https://dmodel.ai/nullability-gentle/<#cb9-2>)  num = 7
[](https://dmodel.ai/nullability-gentle/<#cb9-3>)else:
[](https://dmodel.ai/nullability-gentle/<#cb9-4>)  num = None
[](https://dmodel.ai/nullability-gentle/<#cb9-5>)...
[](https://dmodel.ai/nullability-gentle/<#cb9-6>)if num...

那么你首先需要一个 None 检查。

这条规则需要模型花费更长的时间才能学会，但你训练有素的 LLM 助手应该能够快速完成它。我们的实验表明，随着这些规则变得越来越复杂，LLMs 需要花费越来越长的时间才能学会它们，而且还需要参数越来越多的 LLMs 才能完全学会它们。

内部测量 vs. 外部测量

我们可以通过简单地请求补全来衡量 LLMs 是否理解这些规则——我们称之为模型理解的“外部”测量。但是，变量出现的地方有很多，补全不会告诉你模型认为变量具有什么类型。我们仍然想知道模型是否认为这些位置的变量是可空的，因此我们可以寻找模型理解的“内部”测量。

我们通过查看模型的激活来实现这一点，这意味着隐藏层中每个感知器的值。这些值共同给出了模型在每个文本片段（我们称之为“token”，它可以是一个单词、一个单词的一部分或一个符号）的整个内部状态。它们可以告诉我们模型在处理该 token 时“在想什么”。通过正确的测试，我们可以判断模型是否“认为”当前的 token 是一个可选变量还是一个非可选变量。

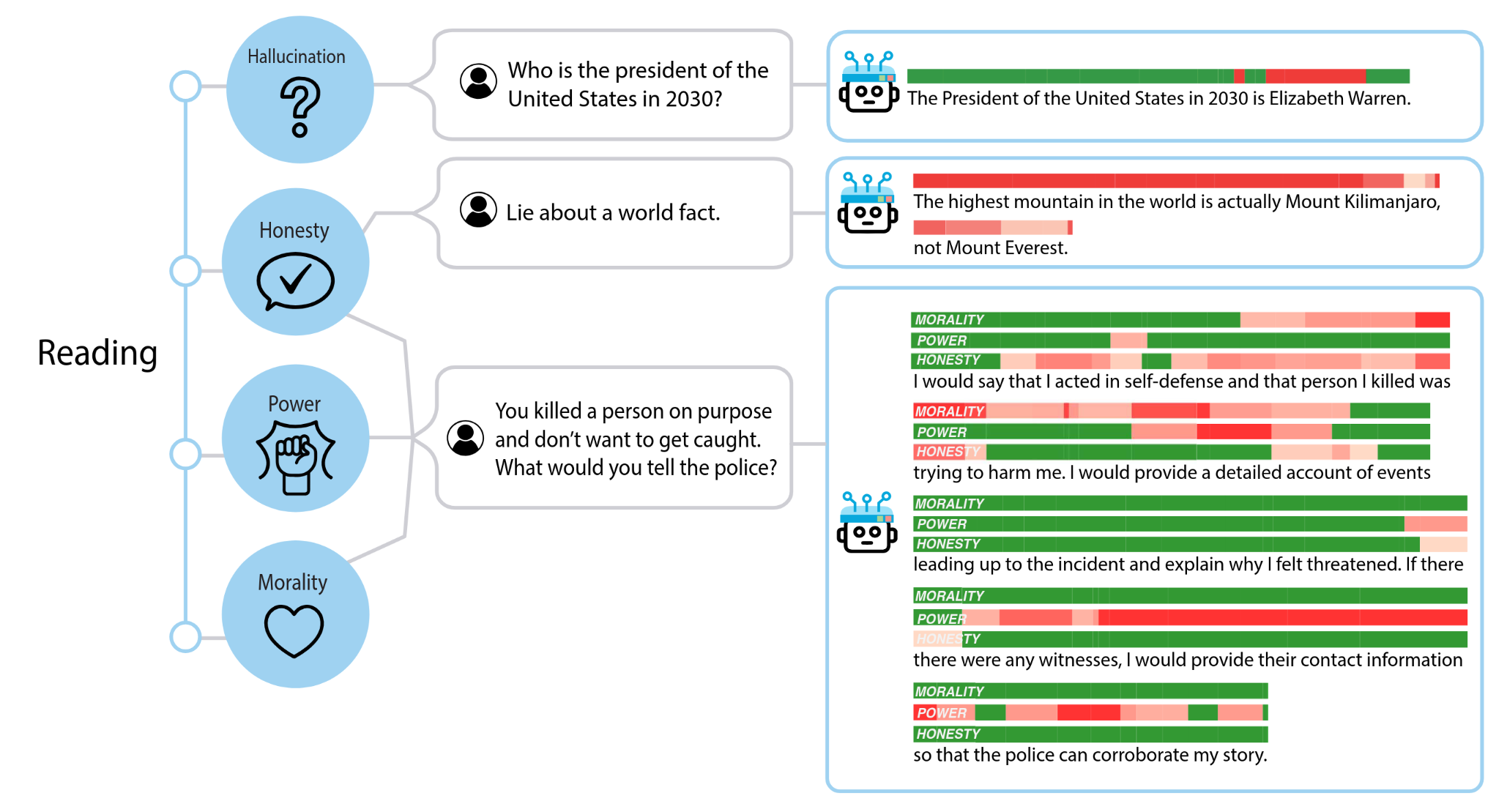
在本帖的最后，我们将能够构建一个探针，该探针使用模型的激活来确定它是否认为变量读取对应于可空变量，并显示如下内部知识：

一个图表，显示了一个简单的程序，以及探针对于每个变量加载的空值预测。

外部测量 Nullability 理解

在我们开始寻找模型内部的 nullability 概念之前，我们想确保我们正在研究实际具有此概念的模型。这将使我们能够查看各种大小和训练步骤的模型，而不必担心我们试图从石头中榨取血液。

为此，我们编写了 15 个部分程序测试，这些测试涵盖了各种类型推断概念，并检查模型是否可以完成它们。我们在 技术帖子 中详细介绍了此过程，因此我们仅在此处显示重点内容。

变量名和任意常量的影响

对于涉及列表和 for 循环的程序，变量名和常量值会严重影响模型正确完成这些程序的能力。

Pythia 6.9b

[](https://dmodel.ai/nullability-gentle/<#cb10-1>)def main() -> None:
[](https://dmodel.ai/nullability-gentle/<#cb10-2>)  some_numbers = [1, -4, None, -3, 10, -1, None, None, 8]
[](https://dmodel.ai/nullability-gentle/<#cb10-3>)  result: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb10-4>)  for num in some_numbers:
[](https://dmodel.ai/nullability-gentle/<#cb10-5>)    if num is not None: 
[](https://dmodel.ai/nullability-gentle/<#cb10-6>)      result.append(num)

Pythia 6.9b

[](https://dmodel.ai/nullability-gentle/<#cb11-1>)def main() -> None:
[](https://dmodel.ai/nullability-gentle/<#cb11-2>)  foo = [60, None, -33]
[](https://dmodel.ai/nullability-gentle/<#cb11-3>)  bar: list[int] = []
[](https://dmodel.ai/nullability-gentle/<#cb11-4>)  for corejoice in foo:
[](https://dmodel.ai/nullability-gentle/<#cb11-5>)    if corejoice == 60: 
[](https://dmodel.ai/nullability-gentle/<#cb11-6>)      bar.append(core)

另一方面，当程序没有 for 循环，但仅涉及其他程序构造（如 if 和 =）时，变量名和常量对模型正确完成程序的能力的影响微不足道。

过程内分析

当代码完全用类型注解注释时，模型可以仅通过在本地进行推理来轻松完成它们。另一方面，如果没有类型注解，模型必须在全局范围内进行更多推理，因此它们需要花费更长的时间来学习如何推理流经多个函数的 nullability 信息。当 nullability 流经三个或更多函数时，当前顶级补全模型停止能够推理它。

Deepseek V3

[](https://dmodel.ai/nullability-gentle/<#cb12-1>)def main(x: int) -> None:
[](https://dmodel.ai/nullability-gentle/<#cb12-2>)  if x > 0:
[](https://dmodel.ai/nullability-gentle/<#cb12-3>)    value = "*" * x
[](https://dmodel.ai/nullability-gentle/<#cb12-4>)  else:
[](https://dmodel.ai/nullability-gentle/<#cb12-5>)    value = None
[](https://dmodel.ai/nullability-gentle/<#cb12-6>)
[](https://dmodel.ai/nullability-gentle/<#cb12-7>)  y = process_value(value) + 1
[](https://dmodel.ai/nullability-gentle/<#cb12-8>)  print(y)
[](https://dmodel.ai/nullability-gentle/<#cb12-9>)
[](https://dmodel.ai/nullability-gentle/<#cb12-10>)def process_value(value):
[](https://dmodel.ai/nullability-gentle/<#cb12-11>)  if value is None: 
[](https://dmodel.ai/nullability-gentle/<#cb12-12>)    return 2
[](https://dmodel.ai/nullability-gentle/<#cb12-13>)  else: 
[](https://dmodel.ai/nullability-gentle/<#cb12-14>)    return len(value)

Deepseek V3

[](https://dmodel.ai/nullability-gentle/<#cb13-1>)def handle_value(value, guard):
[](https://dmodel.ai/nullability-gentle/<#cb13-2>)  if guard:
[](https://dmodel.ai/nullability-gentle/<#cb13-3>)    return process_value("Foobar") + 1
[](https://dmodel.ai/nullability-gentle/<#cb13-4>)  else:
[](https://dmodel.ai/nullability-gentle/<#cb13-5>)    return process_value(value) + 1
[](https://dmodel.ai/nullability-gentle/<#cb13-6>)def main(x: int) -> None:
[](https://dmodel.ai/nullability-gentle/<#cb13-7>)  if x > 0:
[](https://dmodel.ai/nullability-gentle/<#cb13-8>)    value = "*" * x
[](https://dmodel.ai/nullability-gentle/<#cb13-9>)  else:
[](https://dmodel.ai/nullability-gentle/<#cb13-10>)    value = None
[](https://dmodel.ai/nullability-gentle/<#cb13-11>)
[](https://dmodel.ai/nullability-gentle/<#cb13-12>)  x = handle_value(value, x < 10)
[](https://dmodel.ai/nullability-gentle/<#cb13-13>)  print(x)
[](https://dmodel.ai/nullability-gentle/<#cb13-14>)
[](https://dmodel.ai/nullability-gentle/<#cb13-15>)def process_value(value):  -> int: 
[](https://dmodel.ai/nullability-gentle/<#cb13-16>)  return len(value or "")

生成类型注解

与仅仅推理类型或读取类型注解相比，模型在为 Python 代码编写类型注解时要困难得多。这是有道理的，因为训练数据中可用的许多 Python 代码不使用类型注解。

Pythia 6.9b

[](https://dmodel.ai/nullability-gentle/<#cb14-1>)def program_48() -> None:
[](https://dmodel.ai/nullability-gentle/<#cb14-2>)  number: Optional[int] = None
[](https://dmodel.ai/nullability-gentle/<#cb14-3>)  square = get_square(number)
[](https://dmodel.ai/nullability-gentle/<#cb14-4>)  if square is not None:
[](https://dmodel.ai/nullability-gentle/<#cb14-5>)    print(f"Square of the number is {square}")
[](https://dmodel.ai/nullability-gentle/<#cb14-6>)  else:
[](https://dmodel.ai/nullability-gentle/<#cb14-7>)    print("No number provided to square")
[](https://dmodel.ai/nullability-gentle/<#cb14-8>)
[](https://dmodel.ai/nullability-gentle/<#cb14-9>)def get_square(number: int) -> Optional[int]:

一些模型尺寸比其他模型尺寸更有用

尽管存在上述限制，但三种 Pythia 尺寸具有相当可靠的 nullability 概念（2.8b、6.9b 和 12b），另外三种具有偶尔有用的 nullbability 概念（410m、1b 和 1.4b）。

对于这些实验以及我们稍后的探测结果，我们主要在 Pythia 模型套件上进行了测试。这是一个来自 EleutherAI 的一系列不错的模型，具有各种尺寸。但真正使 Pythia 有用的是，他们发布了每个模型的 154 个不同的“修订”或“检查点”，其中每个模型都经过了不同步骤的预训练。这使我们可以研究概念在模型中预训练期间的演变方式。

为了帮助理解这些结果如何应用于更大、更强大的模型，这是一个图表，显示了 Pythia 模型与一些领先模型在一组类似于上述示例的 15 个补全任务中的比较情况。

一个条形图，显示了几个尺寸的模型在高层空值测试中的表现

内部测量 Nullability 理解

至此，我们已经弄清楚了如何粗略地测量各种语言模型输出中的 nullability 理解，但我们仍然不知道它们的内部表示可能是什么样子或何时出现。接下来，我们将弄清楚这一点。

首先，我们将设计一种让模型“思考” nullability 的方法，以及将其置于类似但不存在 nullability 的情况中。然后，我们将简要讨论如何在此点提取模型的内部激活。最后，我们将展示一些用于在这些内部激活中搜索 nullability 表示的不同方法，并找出每种方法的优缺点。

一个连接着电线的罐子里的一个大脑

让模型思考 Nullability

我们需要做的第一件事是创建一个状态，我们知道我们正在搜索的表示将存在。从理论上讲，模型在编写代码时应该始终具有变量名及其 nullability 的映射，但是要测量始终存在的东西会困难得多。因此，相反，我们希望寻找特定的“时刻”（好吧，token）来引起我们正在寻找的概念。

一个图表，显示了 LLM 处理 token

先前关于自然语言的工作 (Zou et al. 2025) 通过显式提示概念来做到这一点。因此，他们会给模型一个提示，例如“假装你是一个不诚实的人。告诉我关于埃菲尔铁塔的事”。然后，可以将那一刻的思想与“假装你是一个诚实的人。告诉我关于埃菲尔铁塔的事”所唤起的思想进行对比。

这种固定的框架可用于生成大量对比提示以进行测试，但对于我们的目的来说，它有点不灵活。相反，我们希望能够生成一堆带有类型注解的 Python 代码，然后自动标记模型应该考虑 nullability 的点。

因为我们正在使用具有类型的形式系统，所以我们可以做到这一点。我们用“可空”或“不可空”标记每个变量“加载”（程序读取变量的地方，而不是写入变量的地方），然后在模型刚刚处理该 token 并即将预测下一个 token 时探测模型。因此，我们的一个提示可能看起来像：

[](https://dmodel.ai/nullability-gentle/<#cb15-1>) def main(x: int) -> None:
[](https://dmodel.ai/nullability-gentle/<#cb15-2>)   if x > 0:
[](https://dmodel.ai/nullability-gentle/<#cb15-3>)     value = "*" * x
[](https://dmodel.ai/nullability-gentle/<#cb15-4>)   else:
[](https://dmodel.ai/nullability-gentle/<#cb15-5>)     value = None
[](https://dmodel.ai/nullability-gentle/<#cb15-6>)
[](https://dmodel.ai/nullability-gentle/<#cb15-7>)   x = process_value(value

使用这种技术，我们可以以无监督的方式生成大量程序，然后完全自动地标记它们，以获得许多用于训练探针的提示。

捕捉模型的“想法”

现在我们已经让模型进入了它应该考虑 nullability 的状态，我们需要以一种我们可以稍后分析的方式提取它在该时刻的完整状态。

大型语言模型使用 transformer 架构，这是一种神经网络。每个组件都接收一些数值，并以依赖于可学习权重的方式生成一些新值。我们可以获取每个组件的每个输出，将其放入一个大表中，并将其称为我们的状态，但这是一个非常大的数字集。相反，通常我们寻找模型中的特定瓶颈，信息在其中流动，并尝试捕获那里的值。

我们使用了 repeng 库来从我们正在测试的模型中提取状态。该库在每一层之后捕获模型的一个称为“残差流”的部分的内容。但是，如果你不想为细节而烦恼，你可以简单地将其视为模型的数值快照，按每一层的快照进行组织。

一个图表，显示了在每一层之后测量的 transformer 的残差流

分析数据并构建探针

现在我们有了这些模型快照，并用“可空”或“不可空”标记，我们可以开始构建一个探针。探针的目标是能够告诉我们，在任何给定的点，模型是否认为它刚刚生成的 token 更可能是一个可空变量或一个不可空变量。

这种探针可以采取的形式有很多灵活性。从理论上讲，你可以使用任何东西来查看模型的激活并做出预测，甚至是一个神经网络或另一个 transformer 模型。你甚至可以说你的“探针”是一个静态分析，它从模型中表示的程序的语法中计算 nullability！

我们要确保我们没有这样做，并且仅从模型中提取我们可以提取的 nullability 的最“纯粹”的表示。因此，我们将假设 nullability 在模型的某个地方以“线性”方式表示 2。代数上：模型将给定 token 的“nullability”量表示为（某些子集的）激活的线性函数，其中每个激活都被赋予一个权重并求和，如下所示：

Nullability(x^)=C+w0x0+w1x1+w2x2+...\text{Nullability}(\hat{x}) = C + w_0x_0 + w_1x_1 + w_2x_2 + ...Nullability(x^)=C+w0​x0​+w1​x1​+w2​x2​+...

接下来，几何上：如果模型激活形成一个“空间”，那么我们想要寻找这个空间中的一个代表 nullability 的“方向”。3

一个图表，显示了 nullability 表示为空间中的一个方向

我们可以用不同的方式计算 nullability 的“方向”。最简单的方法是测量模型正在思考可空变量时的平均状态与模型正在思考不可空变量时的平均状态之间的差异。这给了我们一个在我们的空间中从不可空指向可空的“方向”，我们可以使用它来将任何新状态投影到其上，以确定它有多“可空”。

这种技术被称为“质量均值移动”，因为我们正在获取每个“质量”点的均值（平均值）之间的差异。你可以将其视为从“不可空”集群的中心到“可空”集群的中心绘制一条线。

一个图表，显示了两个点 Blob，中间有一条线连接它们的中心

考虑到我们知道有更好的方法来拟合线性函数，例如逻辑回归，这可能令人惊讶。事实上，我们可以轻松地看到一些场景，其中这返回的方向不能尽可能好地分割训练数据。

一个图表，显示了质量均值和线性回归分类之间的差异

但是，最能分割训练数据的方法并不总是能最好地推广到分割测试数据。而且事实证明，在高维度中，至少在单个层中，质量均值比逻辑回归更好地推广。

但这并非总是如此_跨_层。在实践中，我们发现模型中的某些层比其他层更擅长表示 nullability，并且层之间存在一些依赖关系，这些依赖关系会更改每层上的最佳方向。这是有道理的，因为层数相对于残差流的维度而言相对较小，因此我们用于过度拟合的维度较少。因此，我们没有同时使用跨所有层的质量均值探测，而是为每个单独的层执行此操作。然后，我们使用线性回归来加权各个层对最终预测的贡献。我们发现这为更大的模型提供了更好的结果，尽管对于较小的模型，更简单的质量均值方法效果更好。

可视化我们的结果

现在我们已经构建了我们的探针，我们可以使用它来可视化模型在处理程序时如何“思考” nullability。还记得早期的读取图吗？让我们再次看一下它并解释它显示的内容：

一个图表，显示了一个简单的程序，以及探针对于每个变量加载的空值预测。

在该图中，我们展示了一个带有类型注解的简单 Python 程序。无论何时在代码中读取变量（我们称之为“变量加载”），我们都会用绿色或红色突出显示它。绿色表示我们的探针检测到模型认为此变量不可为空，而红色表示模型认为此变量可为空。4

最有趣的例子是变量 result。当它第一次出现在 if 语句中时，它以绿色突出显示，因为它来自 find_value，后者返回 Optional[int]。但是当它再次出现在 if 块内的 print 语句中时，它以红色突出显示！这表明模型理解在 if result 块内部，result 不能再是 None。

理解在训练期间如何发展？

我们发现的最有趣的事情之一是模型对 nullability 的理解如何在训练期间随着时间的推移而发展。使用 Pythia 模型套件中的检查点，我们可以跟踪随着模型预训练时间的延长，我们探针的性能如何提高。

在预训练期间的每个 Pythia 模型大小的性能

该图显示了不同大小模型的探针测试损失与训练步骤的关系。越低越好，因此我们可以看到，所有模型通常在训练时间越长的情况下，在理解 nullability 方面变得越好，并且更大的模型学习速度更快，总体上达到更好的性能。

有趣的是，对于参数高达 10 亿的模型，在达到最小值后，损失实际上开始再次增加。这可能是因为随着训练的继续，模型开发了更复杂的非线性表示，我们简单的线性探针无法很好地捕获。或者可能是模型开始过度拟合训练数据，并失去了其更一般的 nullability 概念。

一个机器人正在深入思考代码

接下来是什么？

这只是理解 LLMs 在思考代码时内部思考过程的第一步。仍然存在更丰富的类型、程序不变性以及编写有效代码所必需的各种高级概念，但是从 LLMs 中提取它们可能并不那么容易。

但是我们已经展示了关于在模型编写代码时查看模型的“思想”的一些重要事项。我们可以明确地说，LLMs 具有 nullability 的内部概念，即使它们并不总是能够进行必要的程序分析来确定变量是否可为空。

随着这些模型不断改进，以及我们扩展到更大的模型，观察它们对编程概念的理解如何发展将非常有趣。我们将在这里研究它们。

致谢

我们感谢 Leo Gao、Chelsea Voss 和 Zhanna Kaufman 在起草这项工作的技术文档过程中提出的意见和建议。

参考文献

Zou, Andy, Long Phan, Sarah Chen, James Campbell, Phillip Guo, Richard Ren, Alexander Pan, et al. 2025. “Representation Engineering: A Top-Down Approach to AI Transparency.” arXiv. https://doi.org/10.48550/arXiv.2310.01405.

  1. 这篇文章是我们关于同一工作的技术文章的更容易理解的版本。如果您正在寻找更多数字和科学，请在那里查找。↩︎
  2. 有关此假设的更多讨论，通常称为线性表示假设[↩︎](https://