解析组合学 -- 一个完整示例

2025年4月8日 - 标签: sage

又是一天，又一篇以“前几天我在 mse 上看到……”开头的博客文章。这次，有人问了一个有趣的问题，大意是“有多少个具有 $n$ 个节点的_无序_有根三叉树，在同构意义下？”。我非常喜欢这种组合问题，在找到一个生成函数解之后，我想挑战自己，使用 Flajolet–Sedgewick 风格的解析组合学来获得一个渐近近似！我以前从未真正做过这个，所以我学到了很多东西，我想分享我学到的一些东西——特别是如何在 sage 中做这些事情！

现在，你可能会想——你不是在三年前写过一篇非常相似的博客文章吗？是的。我确实写过。我是否也_完全_忘记了那篇文章的内容？是的。是的，我忘记了，哈哈。由于某种原因，我把它和更早的一篇文章混淆了，那篇文章的相关性远不如这一篇。谢天谢地，这没什么大不了的，因为我很确定我想要做的事情无论如何都无法在那篇文章的框架下工作，而且我现在对这个机制_实际在做什么_有了更好的了解，这真的令人兴奋（因为我_一直_想理解这些东西很多年了）。

让我们从一个热身问题开始！我们如何计算具有 $n$ 个节点的有根_有序_三叉树的数量？

这些是你可能在第一堂算法和数据结构课上记住的那种“三叉树”。这样的树要么是一个叶子，要么是一个具有 1、2 或 3 个孩子的内部节点。至关重要的是，这些孩子都有一个_顺序_，因为数据类型会跟踪哪个孩子在左边/右边（在 2 个孩子的情况下）或在左边/中间/右边（在 3 个孩子的情况下）。毕竟，从 CS 的角度来看，我们需要记住这一点才能遍历树！

这意味着以下两棵树对于我们的目的来说是不同的，即使它们作为图是同构的：

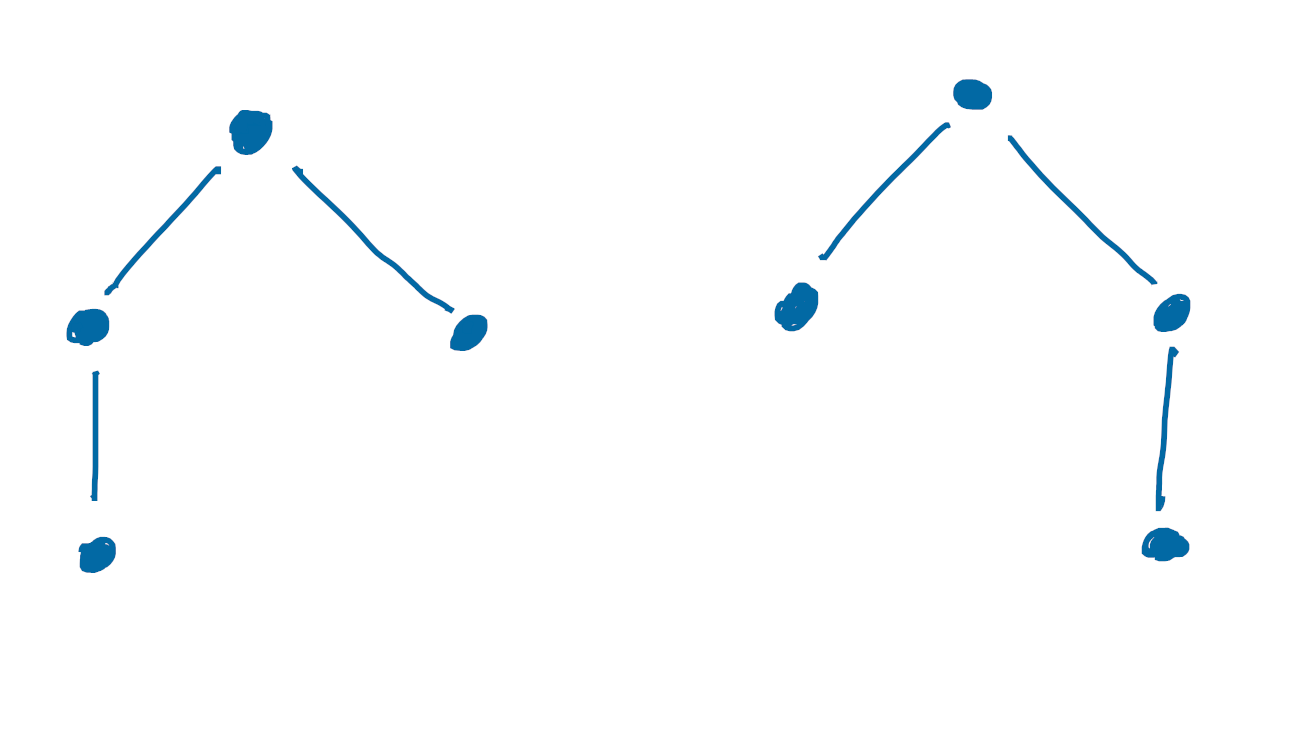
在函数式编程语言中，你可能会用以下方式描述这种数据类型：

T z = Leaf z
  | Unary z (T z)
  | Binary z (T z) (T z) 
  | Ternary z (T z) (T z) (T z)

这可以直接转换为 $t_n$ 的 生成函数 的函数方程，它计算具有 $n$ 个节点的有根有序三叉树的数量： \[T(z) = z + zT + zT^2 + zT^3\] 我们可以将其重新排列为 \[z = \frac{T}{1 + T + T^2 + T^3}\] 这样我们就可以通过 lagrange 反演 计算 $T$ 的幂级数展开式：

xxxxxxxxxx

1

R.<z> = QQbar[[]] # power series ring

2

T = (z/(1 + z + z^2 + z^3)).reverse()

3

show(T.O(10))

Evaluate Language: Sage Gap GP HTML Macaulay2 Maxima Octave Python R Singular Messages 令人难以置信的是，这与 A036765 一致，正如我们所希望的那样，它是“具有 n 个非根节点且所有出度 <= 3 的有序有根树的数量”！

你可能会合理地问，这些数字是否有闭合形式，但这要求太高了（实际上，要求斐波那契数列的闭合形式已经太高了，而且这_更_复杂）。但与斐波那契数列一样，我们可以得出一个极好的近似值： \[t_n = [z^n] T \approx C \frac{(3.6107\ldots)^n}{n^{3/2}} \left (1 \pm O \left ( \frac{1}{n} \right ) \right )\] 其中 $C = \frac{(0.8936\ldots)}{2 \sqrt{\pi}}$ 是一个常数。

事实上，这给出了_极好的_结果！让我们绘制这个近似值与真实值的比率，以便我们可以看到随着 $n$ 变大，这个近似值变得有多好。请注意，它也尊重承诺的 big-oh 误差界！

xxxxxxxxxx

1

def actual(n,N):

2

  R.<z> = PowerSeriesRing(QQbar, default_prec=N)

3

  T = (z/(1 + z + z^2 + z^3)).reverse()

4

  return T.coefficients()[n-1:]

5

​

6

def approx(n,N): 

7

  # very very magic

8

  C = 0.8936373911078061 / (2 * sqrt(pi))

9

  w = 3.610718613276040

10

  return [(C * w^k * (1/k^1.5)).n() for k in range(n,N+1)]

11

​

12

show(html("Plot the error ratios in the range [n,N]"))

13

@interact

14

def _(n=input_box(100, width=20, label="$n$"),

15

   N=input_box(120, width=20, label="$N$"),

16

   auto_update=False): 

17

​

18

  actuals = actual(n,N)

19

  approxs = approx(n,N)

20

  ratios = [(actuals[i]/approxs[i]) for i in range(N+1-n)]

21

  show(html("ratio at n={}: {}".format(n, ratios[0])))

22

  show(html("ratio at N={}: {}".format(N, ratios[-1])))

23

​

24

  text_options = {'horizontal_alignment': 'right',

25

          'vertical_alignment': 'bottom', 

26

          'fontsize': 'large'}

27

​

28

  G = Graphics()

29

  G += scatter_plot([(n+i,r) for (i,r) in enumerate(ratios)])

30

  G += plot(1, (x,n,N))

31

  G += plot(1-1/x, (x,n,N))

32

  G += text('$y = 1$', (N, 1), **text_options)

33

  G += text('$y = 1-1/x$', (N, 1-1/N), **text_options)

34

​

35

  G.show()

Evaluate Language: Sage Gap GP HTML Macaulay2 Maxima Octave Python R Singular Messages 这非常酷，但是_这个近似值到底是从哪里来的_？

答案被称为奇点分析，可以在 Melczer 的优秀著作 An Invitation to Analytic Combinatorics 的第 2 章第 3 节中找到，或者在 Flajolet 和 Sedgewick 的 巨著 的第 VI 和 VII 章中找到。特别参见第 468 页上的定理 VII.3。

就像复分析中似乎每个定理一样，这基本上是 留数定理 的应用。我不会过多地解释它为什么有效，但我至少会做一个证明的姿态。如果你想要更精确的东西，你可以阅读上面的参考资料。

首先，我们回顾 \[t_n = \frac{1}{2\pi i} \int_C \frac{T}{z^{n+1}} \ \mathrm{d}z\] 其中 $C$ 是包含原点的 $T$ 是全纯的区域内的任何轮廓。

然后我们画出复分析中最重要的图：

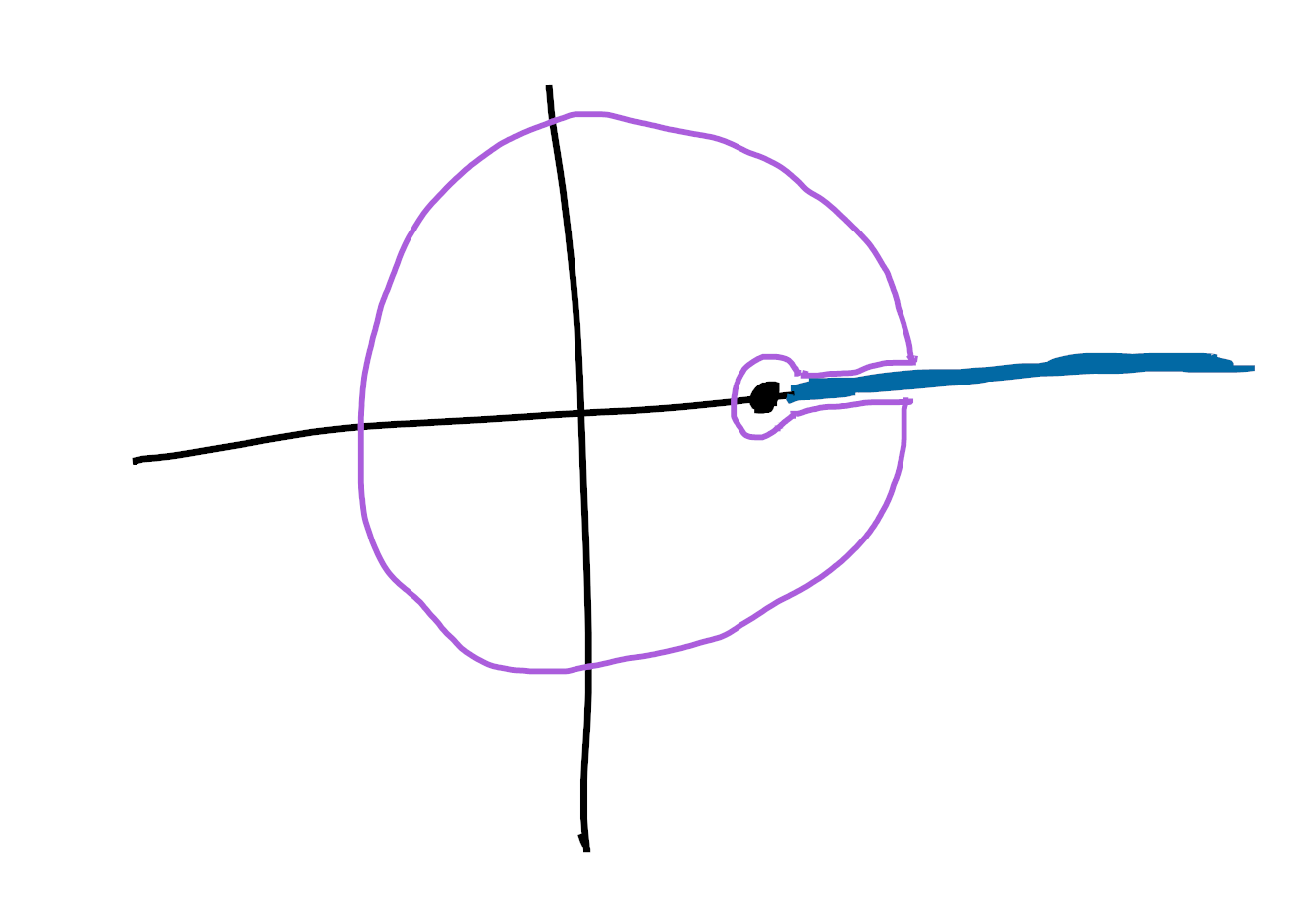
这里明显的标记点是我们的奇点 $\omega$，我们为 $T$ 选择了一个 分支切割 （以蓝色显示1)，以便 $T$ 在粉红色曲线所在的区域内是全纯的。我们将通过估计大圆、小圆和两个水平部分的贡献来估计这个积分的值[2](https://grossack.site/2025/04/08/<#fn:5>）。

事实证明，两个水平部分基本上对我们的积分贡献了 $O(1)$ 的量，所以我们忽略它们。由于大圆是紧凑的，$T$ 将在它上面达到最大值，比如说 $M$。那么沿着大圆（比如说半径为 $\omega + \epsilon$）的积分以 $2 \pi (\omega + \epsilon) \frac{M}{(\omega + \epsilon)^{n+1}} = O((\omega+\epsilon)^{-n})$ 为界。

为了估计围绕小圆的积分，如果我们在 $\omega$ 处有一个级数展开式会很有帮助，因为我们离它很近……不幸的是，$\omega$ 是一个奇异点，所以我们没有泰勒级数，但_幸运的是_有一个工具专门用于这项工作：一个 Puiseux 级数！

我不会过多地谈论这些是什么，特别是因为 Richard Borcherds 已经发布了一个 很棒的视频 关于这个主题。重要的是 Sage 可以为我们计算它们3，所以我们可以真正掌握近似值！

我们计算围绕小圆的积分大致为： \[\begin{align} \frac{1}{2 \pi i} \int \frac{T}{z^{n+1}} \ \mathrm{d}z &\overset{(1)}{\approx} \frac{1}{2 \pi i} \int \frac{c_\alpha (1-\frac{z}{\omega})^\alpha}{z^{n+1}} \ \mathrm{d}z \\ &\overset{(2)}{=} \frac{1}{2 \pi i} \int \frac{c_\alpha \sum_k \binom{\alpha}{k} (\frac{-z}{\omega})^k}{z^{n+1}} \ \mathrm{d}z \\ &\overset{(3)}{=} c_\alpha \binom{\alpha}{n} \frac{(-1)^n}{\omega^n} \end{align}\] 在步骤 $(1)$ 中，我们用它的 Puiseux 级数的第一项来近似 $T$，在步骤 $(2)$ 中，我们应用 广义二项式定理，以便在步骤 $(3)$ 中，我们可以应用留数定理来实现这个积分作为我们的 laurent 展开式中 $z^{-1}$ 的系数。

这给了我们一些像 $\widetilde{O}(\omega^{-n})$ 一样增长的东西，支配了来自大圆的贡献 $O((\omega + \epsilon)^{-n})$，所以渐近地这是唯一重要的项。如果我们更小心地跟踪 $T$ 的 Puiseux 级数的 big-oh 误差，我们可以很容易地锐化这个界4，看到 \[t_n = c_\alpha \binom{\alpha}{n} \frac{(-1)^n}{\omega^n} \left ( 1 + O \left ( \frac{1}{n} \right ) \right )\] 这个带 $(-1)^n$ 的表达式看起来有点奇怪，但请记住 $\binom{\alpha}{n}$ 也交替符号。事实上，$\binom{\alpha}{n}$ 的渐近线是 众所周知的，因此我们可以将其重写为 \[t_n = \frac{c_\alpha}{\Gamma(-\alpha)} \frac{\omega^{-n}}{n^{\alpha + 1}} \left ( 1 + O \left ( \frac{1}{n} \right ) \right )\] 这终于向我们展示了我们的神奇数字来自哪里！Sage 很高兴地告诉我们 $T$ 的主要奇点在 $\omega = (0.2769\ldots)$ 处，并且 $T$ 在 $\omega$ 处的 Puiseux 展开式为 \[T \approx (0.65\ldots) - (0.8936\ldots) (1-z/\omega)^{1/2} + \ldots\] 因此对于我们来说，$\alpha = 1/2$，并且 $C_{1/2} = -(0.8936\ldots)$。

最后，由于 $\Gamma(-1/2) = -2 \sqrt{\pi}$ 并且 $(0.2769\ldots)^{-1} = (3.6107\ldots)$ 我们看到 \[t_n = \frac{(0.8936\ldots)}{2 \sqrt{\pi}} \frac{(3.6107\ldots)^{n}}{n^{3/2}} \left ( 1 + O \left ( \frac{1}{n} \right ) \right )\] 正如承诺的那样！

事实上，这就是你如何让 sage 为你做所有这些事情！

xxxxxxxxxx

1

# at time of writing the abelfunctions package

2

# isn't installed on sagecell, so you'll need to 

3

# run this locally if you want to play with it

4

import abelfunctions

5

​

6

# to compute the discriminant we need P to be a 

7

# polynomial whose coefficients are polynomials.

8

R.<z> = QQbar[]

9

S.<T> = R[]

10

​

11

# our defining polynomial. 

12

# we want to solve for T as a function of z

13

P = z*T^3 + z*T^2 + (z-1)*T + z

14

​

15

# following Example 2.12 in Melczer,

16

# we compute the dominant singularity w. 

17

w = min([r for (r,_) in P.discriminant().roots() if r != 0], 

18

    key=lambda r: r.abs())

19

​

20

# to work with abelfunctions we need P 

21

# to be a polynomial in two variables

22

R.<z,T> = QQbar[]

23

P = R(P)

24

​

25

# compute the puiseux expansion for T at w. 

26

# I know from trial and error that the correct 

27

# branch to pick is entry [1] in the list. You 

28

# just need to check which one gives you 

29

# positive real coefficients for T at 0.

30

s = abelfunctions.puiseux(P,w)[1]

31

c = -sqrt(-s.x0/s.xcoefficient)

Evaluate Language: Sage Gap GP HTML Macaulay2 Maxima Octave Python R Singular Messages 作为一个有趣的练习，你可以修改这段代码（使用 s.add_term()）来计算更长的 puiseux 级数，并获得对有根三叉树的数量有效的渐近线，直到一个 $O \left ( \frac{1}{n^2} \right )$ 的乘法误差。

尝试修改前面的代码块以查看我们当前的近似值_不_准确到 $O \left ( \frac{1}{n^2} \right )$，然后检查你的近似值_是_否准确！

好的，现在我们理解了热身，让我们开始解决实际问题！

有多少个_无序的_有根三叉树，直到同构？

现在我们要计算到图同构，所以我们的两棵树 现在_被认为_是同构的。实际上，如何确定像这样的东西的生成函数并不那么明显，但幸运的是，答案来自 Pólya-Redfield 计数！如果这对你来说是新的，你可能会对我的最近的 博客文章 感兴趣，我在其中谈到了一些它的推论。但是今天，我们将以一种更复杂的方式使用它。

假设你有一个结构 $X$，它受到群 $G$ 的作用，以及一个“颜色”的集合 $C$。我们如何计算在 $G$ 的作用下，为每个 $x \in X$ 赋予一种来自 $C$ 的颜色的方式的数量？

我们首先构建作用 $G \curvearrowright X$ 的 循环指标多项式，我们称之为 $P_G(x_1, \ldots, x_n)$。然后我们可以将各种各样的东西插入到变量 $x_i$ 中，以解决各种计数问题。例如，如果 $C$ 实际上只是一个有限的颜色集，我们可以插入 $x_1 = x_2 = \ldots = x_n = |C|$ 来恢复我最近的博客文章中的表达式。但我们也可以做更多的事情！

假设 $C$ 是一系列可能无限的允许的“颜色”，每种颜色都有一个固定的“权重”。（对于我们来说，我们的“颜色”将是树，而“权重”将是节点的数量）。然后我们可以将它们排列成一个生成函数 $F(t) = \sum c_i t^i$，其中 $c_i$ 计算权重为 $i$ 的颜色的数量[5](https://grossack.site/2025/04/08/<#fn:11>）。然后一个简单的论证（在 wikipedia 页面 上给出了完整信息）表明 $P_G(F(t), F(t^2), \ldots, F(t^n))$ 是一个生成函数，用于计算用来自 $C$ 的颜色着色 $X$ 的方式的数量，在 $G$ 作用下计数，并按其总权重排序6。查看 wikipedia 页面以获取大量很棒的示例！

对于我们来说，我们意识到一个无序的有根三叉树要么是空的，要么是一个带有 3 个递归孩子的根7。在递归情况下，我们还希望计算直到明显的 $\mathfrak{S}3$ 作用，该作用排列孩子，因此通过前面的讨论我们了解到 \[T(z) = 1 + z P{\mathfrak{S}3}(T(z), T(z^2), T(z^3))\] 其中 \(P{\mathfrak{S}_3}(x_1, x_2, x_3) = \frac{1}{6}(x_1^3 + 3x_1 x_2 + 2 x_3)\) 是三个字母上的对称群的循环指标多项式。将其插入后我们看到 \[T(z) = 1 + \frac{z}{6} \left ( T(z)^3 + 3 T(z) T(z^2) + 2 T(z^3) \right )\] 现在，我们如何使用这个函数方程获得 $t_n$ 的渐近线？

首先让我们考虑一下我们对热身问题的解决方案是如何工作的。我们写 $F(z,T)=0$，其中 $F$ 是一个多项式，使用隐函数定理得到 $T$ 在原点的泰勒级数，然后在主要奇点 $\omega$ 附近得到一个 Puiseux 级数，这让我们能够准确地估计泰勒系数 $t_n$[8](https://grossack.site/2025/04/08/<#fn:14>）。

我们将在这里玩同样的游戏，除了我们将假设 $F$ 仅仅是_全纯的_而不是多项式。因为我们不再使用多项式，这似乎真的需要无限量的数据，所以我不知道如何获得相关常数的精确解……但按照 Flajolet 和 Sedgewick 的 VII.5 节，我们可以得到我们想要的数值解！

我们将假设函数 $T(z^2)$ 和 $T(z^3)$ 已经是已知的解析函数，因此我们可以写 $F(z,w) = -w + 1 + \frac{z}{6} \left ( w^3 + 3 T(z^2) w + 2 T(z^3) \right )$。这是一个满足 $F(z,T) = 0$ 的解析函数。

现在来点魔法。假设我们可以找到一对 $(r,s)$，使得 $F(r,s)=0$ 和 $\left . \frac{\partial F}{\partial w} \right |{(r,s)} = 0$……那么 $F$ 在 $w$ 方向上在 $(r,s)$ 处是奇异的，所以这是 $T$ 的一个分支点。由于 $F$ 和 $F_w = \frac{\partial F}{\partial w}$ 都在 $(r,s)$ 处消失，因此 $F$ 在 $(r,s)$ 处的泰勒级数从 \[F_z(r,s) (z-r) + \frac{1}{2} F{ww}(r,s) (w-s)^2\] 开始。由于我们知道 $F(z,T)$ 消失，我们估计直到较小的阶数项 \[F_z(r,s) (z-r) + \frac{1}{2} F_{ww}(r,s) (T-s)^2 = 0\] 因此 $T$ 在 $(r,s)$ 处的 Puiseux 级数开始 \[T = s \pm \sqrt{\frac{2r F_z(r,s)}{F_{ww}(r,s)}} \left ( 1 - \frac{z}{r} \right )^{1/2}\] 如果我们写 $\gamma = \sqrt{\frac{2r F_z(r,s)}{F_{ww}(r,s)}}$ 并且对我们的误差项更加小心，则来自热身的相同技术显示 \[t_n = \frac{\gamma}{\Gamma(-1/2)} \frac{r^{-n}}{n^{3/2}} \left ( 1 + O \left ( \frac{1}{n} \right ) \right )\] 有关此定理的更仔细的证明，请参见 Flajolet 和 Sedgewick 第 468 页上的定理 VII.3。

现在我们如何_使用_它？我们可以通过 $T$ 在原点的泰勒级数来近似 $T$，然后使用这个近似值来数值求解方程组 $F(r,s) = F_w(r,s) = 0$ 的唯一9正实数解：

xxxxxxxxxx

1

# how far we taylor expand T. This controls the accuracy 

2

# of our approximation of (s,r).

3

# the sagecell times out if you make this too big, so you 

4

# might want to run this locally.

5

N = 5

6

​

7

# get the first n taylor coefficients for T

8

def approx(n):

9

  B = PolynomialRing(QQ, 't', n+1)

10

  t = B.gens()

11

  R.<z> = B[[]]

12

​

13

  # cycle index polynnomials

14

  S.<x1,x2,x3> = QQ[]

15

  P3 = (x1^3 + 3*x1*x2 + 2*x3)/6

16

​

17

  # to start, the taylor coefficients of T are variables

18

  T = sum([t[i] * z^i for i in range(n)]) + O(z^n)

19

​

20

  lhs = T

21

  rhs = 1 + z*P3.subs(x1=T(z), x2=T(z^2), x3=T(z^3))

22

​

23

  # formally expand out the rhs and set the coefficients 

24

  # equal to each other. This gives a recurrence relation 

25

  # for t[n] in terms of the t[i] for i<n. 

26

  # Then we solve this recurrence via groebner bases, 

27

  # which is extremely fast.

28

  I = B.ideal([lhs.coefficients()[i] - rhs.coefficients()[i] 

29

         for i in range(n)])

30

​

31

  # add all our solved coefficients back together to 

32

  # get an approximation for T

33

  return sum([I.reduce(t[i])*z^i for i in range(n)]) + O(z^n)

34

​

35

z,w = var('z,w')

36

T = SR(approx(N).truncate())

37

F = -w + 1 + (z/3)*T.subs(z=z^3) + (z/2)*T.subs(z=z^2)*w + (z/6)*w^3

38

​

39

eqns = [diff(F,w)==0, F==0]

40

solns = [[a.rhs(), b.rhs()] for [a,b] in solve(eqns,[z,w])]

41

realSolns = [[a,b] for [a,b] in solns if a in RR and b in RR]

42

[r,s] = realSolns[0]

43

​

44

show(html("$r={}$".format(r)))

45

show(html("$s={}$".format(s)))

46

​

47

gamma = -sqrt(2*r*diff(F,z).subs(z=r,w=s)/diff(F,w,2).subs(z=r,w=s))

48

​

49

show(html("$\\gamma={}$".format(gamma)))

Evaluate Language: Sage Gap GP HTML Macaulay2 Maxima Octave Python R Singular Messages 如果我们在本地运行这段代码，其中 $N=20$，我们会得到近似值 \[\begin{align} r &\approx 0.3551817478731632 \\ s &\approx 2.1174205967276225 \\ \gamma &\approx -1.8358222405236164 \end{align}\] 因此我们期望 \[t_n \approx \frac{(1.835\ldots)}{2 \sqrt{\pi}} \frac{(0.355\ldots)^{-n}}{n^{3/2}}\] 事实上，这似乎效果很好！我们对 $T$ 的泰勒展开与 A000598 一致，正如我们所期望的那样，并且将我们的近似值与我们的泰勒展开进行比较给出：

xxxxxxxxxx

1

r = 0.3551817478731632

2

s = 2.1174205967276225

3

gamma = -1.8358222405236164

4

​

5

def approx(n):

6

  return (gamma / (-2 * sqrt(pi))) * (r^(-n) / n^(3/2))

7

​

8

def approxList(n,N):

9

  return [approx(k) for k in range(n,N)]

10

​

11

def actualList(n,N):

12

  B = PolynomialRing(QQ, 't', N+1)

13

  t = B.gens()

14

  R.<z> = B[[]]

15

​

16

  S.<x1,x2,x3> = QQ[]

17

  P3 = (x1^3 + 3*x1*x2 + 2*x3)/6

18

​

19

  T = sum([t[i] * z^i for i in range(N)]) + O(z^N)

20

​

21

  lhs = T

22

  rhs = 1 + z*P3.subs(x1=T(z), x2=T(z^2), x3=T(z^3))

23

​

24

  I = B.ideal([lhs.coefficients()[i] - rhs.coefficients()[i] 

25

         for i in range(N)])

26

​

27

  return [I.reduce(t[i]) for i in range(n,N)]

28 29

show(html("Plot the error ratios in the range [n,N]"))

30

show(html("This is likely to time out if you make N too large online,"))

31

show(html("so you might want to play around with it locally instead!"))

32

@interact

33

def _(n=input_box(10, width=20