在约束求解器中处理无限性:挑战与应对 (Grappling with Infinity in Constraint Solvers)
在约束求解器中处理无限性:挑战与应对 (Grappling with Infinity in Constraint Solvers)
Published November 17, 2019 by Chris Patuzzo
2016年,我创建了一种名为 Sentient 的编程语言。 从那时起,我花时间反思并思考了这门语言。这个系列文章就是关于这些思考的。
许多约束满足问题都以某种形式涉及无限性。 即使是像“找到两个加起来等于 10 的整数”这样的基本问题,其解也包括:
- (4, 6)
- (-7, 17)
- (-1953856112, 1953856122)
这个升级速度有点快!
事实上,存在无限多的解和无限多对整数需要测试。 这是一个用 Sentient 编写的程序来解决此问题:
int a, b;invariant a + b == 10;expose a, b;
▲ 一个寻找和为10的整数的 Sentient 程序
本文是关于 Sentient 的,但许多概念普遍适用于约束求解器。
我们可以使用 [--number 0 option](https://tuzz.tech/blog/https:/sentient-lang.org/cli/number) 运行它,以连续查找解决方案:
当 Sentient 返回 {} 时,它已经穷尽了搜索空间,无法找到更多解决方案。
几秒钟后,该程序终止,这似乎_不对劲_。 为什么一个有无限多解的问题会终止? 它不应该永远运行吗?
我有时会同义地使用“程序”和“问题”。 程序是对问题的描述。
简单的答案是,Sentient 中的整数并不是数学定义中的真正整数。 它们的幅度受到表示它们的位数限制。 默认情况下,这是 8 位,但可以指定,例如 int9、int32。
int 的范围从 -128 到 127。
在许多情况下,这没问题。 我们可以选择一个“足够大”的位数而不必担心它。 但在其他时候,这就不行了。 我们经常想从小处着手,逐步增加表示范围,但这意味着每次都要重新启动程序。
对于某些问题,解决方案极其罕见(或不存在),Sentient 可能需要数周或数月才能找到一个解决方案。 在这些情况下,从较小的表示开始,逐步排除越来越大的搜索空间是有意义的。
对于较小空间的否定结果优于对较大空间没有结果。
不幸的是,当程序重新启动时,我们失去了它的进度。 已经探索过的区域会被再次探索。 如果我们将 int 增加到 int9,Sentient 会找到新的解决方案,但也会再次找到所有相同的解决方案。 这是浪费。
我们可以通过添加约束来补偿:
int9 a, b;invariant a < -128 || a > 127 || b < -128 || b > 127;# ...
▲ 消除我们已经探索过的区域
但这变得笨拙,并且对于许多问题来说,不容易指定。 这也是一个手动过程,因此容易出错。 理想情况下,Sentient 会为此类事物提供一流的支持。 我对它如何工作有一些想法。
这指定 a 或 b 必须位于已探索的八位整数的区域之外。
在 一些情况下,我 编写了脚本 来生成具有越来越大整数的 Sentient 程序。
近似值 (Approximations)
我发现一种有用的思考方式是从_近似值_的角度来看待它。 八位整数实际上是数学(无限)版本的整数的近似值。 它的域是有限的,但只要我们保持在界限内,它的行为方式相同。
我正在以_字面_意义使用“近似值”,而不是根据一些精确的数学定义。
大多数时候,当我们编写计算机程序时,我们不必考虑这一点,因为我们处理具体化。 变量被赋予具体的值,并且只要我们保持在范围内而不溢出,一切都会检查出来。
在我们的例子中,变量是“符号化”的。 我们实际上并没有为 int a, b 分配值,我们只是告诉 Sentient 它们存在并指定一些约束。 它的工作是发现 a, b 的值,但它必须处理一些有形的东西。 它无法推理无限。
“符号化”是 KLEE 项目用于这个概念的术语。
为什么 Sentient 不能推理无限?
好问题!
从技术上讲,它可以,但目前,它的实现与其用于求解的机制密切相关。 程序被编译成 SAT 的实例,根据定义,它是包含有限多个变量和子句的布尔方程。
但这并非必须如此。 Sentient 可以抽象这些方程并自动引入新变量来表示更大的整数。
我认为这可以_更好地逼近_整数的无限版本。
实际上,Sentient 对 [--number option](https://tuzz.tech/blog/https:/sentient-lang.org/cli/number) 做了类似的事情。 Sentient 通过重复求解相同的方程来查找问题的多个解决方案。 它每次都会引入一个新的子句来禁止它刚刚找到的解决方案。
Sentient 不自己求解这些方程。 它委托给 SAT 求解器,例如 lingeling。
我们可以动态地更改表示的大小吗?
我们可以,但如何做到这一点并不明显。 如果一个程序声明了多个整数,我们应该一次性更改它们的位数还是逐个更改? 例如,我们应该一次性将 a 和 b 增加到 int9,还是先增加 a 再增加 b?
对于某些问题,大小上的差异可能很重要:
int a, b;int15 target;invariant a * b == target;expose a, b, target;
这个程序包含隐式知识,即在 -128 到 127 范围内乘以两个数字会得到一个在 -16,384 到 16,383 范围内的数字。 每次我们将 a 和 b 的表示增加一位时,我们_可能应该_将 target 的表示增加两位。
从技术上讲,我们应该使用 int16,因为 -128 x -128 是 16,384,它刚好位于 -2^14 到 2^14 - 1 之外。
更重要的是,我们还没有考虑更复杂的情况。 整数数组或数组的数组呢? 我们还需要考虑 Sentient 如何沟通它的进度。 它到目前为止已经穷尽了哪些搜索空间的区域?
更多无限 (More infinity)
在我们尝试回答其中一些问题之前,让我们首先考虑一下无限可能出现的其他地方。 在 Numberphile 上有一个 很棒的系列 关于寻找三个立方体加起来等于目标数字的问题。 让我们用它来帮助推理。
Brady 也在 这个视频 中与 Adam Savage 讨论了这个问题。
这是一个用 Sentient 编写的程序来解决这个问题:
int a, b, c, target;invariant a.cube + b.cube + c.cube == target;expose a, b, c, target;
▲ 一个寻找三个立方体加起来等于目标的程序
我们可以硬编码 target,但这使得程序更通用。 我们可以 在运行时分配它的值 。
首先,假设我们要进一步推广我们的程序。 如果我们能够编写一个将 N 个立方体相加的程序,而不是将三个立方体相加,那就太好了。 如果我们愿意,可以在运行时分配 N,或者将其保留为未指定。
这不是有效的语法,但这样的程序可能看起来像:
array<int> numbers;int target;invariant numbers.map(*cube).sum == target;expose numbers, target;
▲
一个寻找 N 个立方体加起来等于目标的程序
这不是有效的,因为你必须指定数组的大小,例如
array3<int> numbers;
此外,为什么指数应该是固定的? 如果也可以在运行时分配该值或将其保留为未指定以获得额外的自由度,那就太棒了。
该程序可能如下所示:
array<int> numbers;int target, exp;invariant numbers.map(*pow, exp).sum == target;expose numbers, target, exp;
▲
一个寻找 N 个数字的幂加起来等于目标的程序
这进一步偏离了 Sentient 的语法,因为 map 不支持将参数传递给函数指针,但希望你能明白我的意思。
也许这太泛泛了,但请考虑一下:只需四行代码,我们就能够编写一个程序来解决各种 丢番图方程 。 我觉得这很诱人。 这将是我们向机器传达意图的能力的胜利。
但它可以实现吗?
这与近似值如何匹配?
如果我们在近似值的上下文中考虑这些情况,则固定大小的数组可以被视为对无限大小的通用数组的近似。 我们可以通过运行多个具有不同大小的程序来近似一个通用数组。
有无限多种数组大小需要尝试,也有无限多个指数。 这些情况与之前的情况略有不同,因为搜索空间没有重叠。 九位整数_包含_所有八位整数,但“平方”和“立方”是_不同的_问题。
一些近似导致包含层次结构,另一些定义独立空间。
多维空间 (Multi-dimensional space)
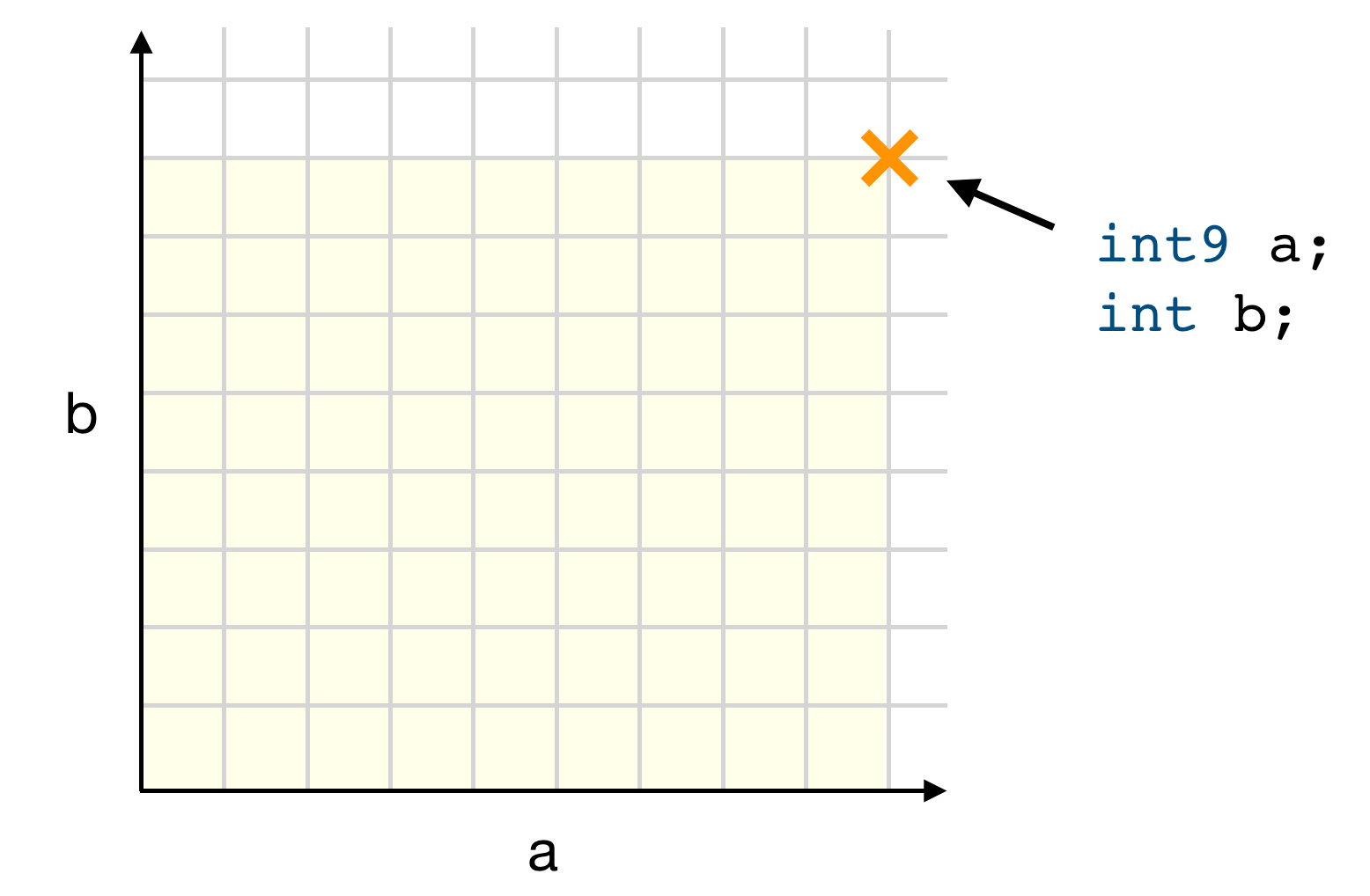
对于每个近似值,我们可以将它们视为定义了空间中的一个维度。 例如,这是一个整数 a 和 b 的二维空间:
突出显示的点是用九位和八位分别近似的整数 a 和 b 的 Sentient 程序的实例。 阴影区域显示了正在考虑的空间,其中包括位数较少的整数。 轴延伸到无穷远。
对于具有不同搜索空间的近似值,不会有阴影区域 - 只有点或线。
整数近似值定义区域是因为 int9 包含 int、int7、int6 等。
_这个_空间的大小并不代表搜索空间的大小,每次我们向近似值添加一位时,搜索空间的大小都会增加一倍。
每次我们近似一个整数时,这都会向我们的空间添加一个新的维度。 如果我们使用不同的近似值多次运行 Sentient 程序,我们可以将其视为定义了通过这个多维空间的行走或路径。
无限维空间 (Infinite-dimensional space)
我们上面非常通用的程序包含这一行:
array<int> numbers;
这里有两种无限。 数组可以具有无限大小,并且整数可以任意大。 这是有问题的,因为我们首先需要近似数组的大小,然后近似该数组中的整数。
这两个自由度的结果是一个无限维空间,每个可能的数组大小都有一个维度。 该空间中的第 n 个维度定义了用于近似数组中位置 n 处的整数的位数。
当我们添加更多近似值时,这些空间会复合,并且这种空间隐喻开始崩溃。 我不确定当我们超过少量维度时,以这种方式思考近似值是否有用。
当我想到整数数组的数组时,我头疼。
增量性 (Incrementality)
现在让我们回到如何随时间改变近似值的问题。 除了像 循环赛 (round-robin) 这样简单的方法之外,似乎没有明显的方法。 具有重叠/非重叠空间的近似值使事情变得更加复杂。
在我看来,最稳健的方法是将这些决定委托给程序员。 定义一个_协议_,以便程序可以确定在搜索的各个阶段应如何更改近似值。
这个程序甚至可以要求用户输入来决定该怎么做。
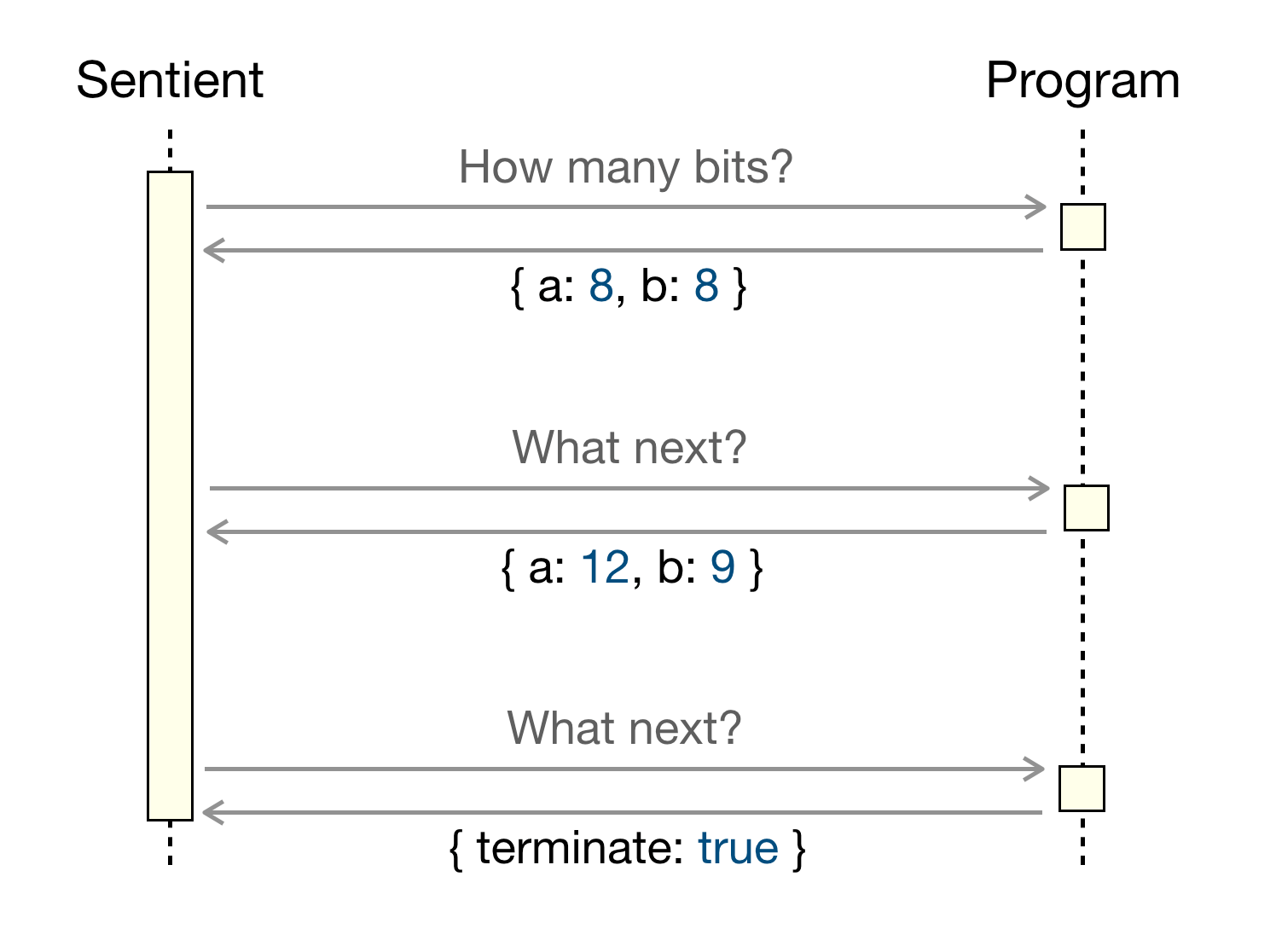
例如,我们“找到两个加起来等于 10 的整数”的程序最初可以调用一个外部程序,该程序指示它使用多少位来表示其近似值。 一旦搜索空间耗尽,它就可以询问程序下一步该怎么做:
或者它可以按时间间隔或在找到每个解决方案后询问。
Sentient 可以将其他信息发送到程序,例如:
- 找到的解决方案以及花费的时间
- 每个近似值对搜索空间的影响
- 近似值是否具有重叠空间
该协议甚至可以允许 Sentient 产生新的进程并并行搜索不同的空间。 例如,它可以同时搜索“平方”和“立方”问题的解决方案,同时控制每个实例中的近似值。
从历史上看,很难 有效地并行化 SAT 求解,因此该策略可能效果很好。
增量 SAT (Incremental SAT)
在 SAT 求解领域,已经存在一种机制,用于在搜索期间与求解器进行通信。 它被称为“可重入增量可满足性应用程序编程接口”,并以其反向首字母缩写词“IPASIR”表示。
IPASIR 首次在 本文 的 6.2 节中介绍。
事实上,不久前我编写了一个 Rust crate 用于通过此接口进行通信。 使用它的优势在于可以加快求解以小方式修改的问题的速度,而无需每次都从头开始重新启动搜索:
可以独立解决此类问题,但是,与增量 SAT 求解器相比,这可能非常低效,后者可以重用在求解先前实例时获得的知识。 – SAT Race 2015 (缩写)
目前,Sentient 根本不使用 IPASIR。 当我编写该语言时,它还相当新,但今天已被更广泛地采用。 至少,它可以加快搜索问题多个解决方案的速度,但我认为它也可以帮助处理近似值。
理想情况下,SAT 问题的单个实例会在 Sentient 程序的整个生命周期内存在。 随着近似值的变化,底层的布尔方程也会发生变化。 这将允许最大量的信息或“知识”被重用。
从理论上讲,这意味着重叠的搜索空间不会被多次探索。
表示 (Representations)
可以对 IPASIR 做的事情有一些限制,否则求解器很难重用先前搜索中的知识。 例如,你不能删除子句,但你可以改为做出短期的“假设”。
你可以通过向要删除的每个子句添加一个子句来_有效_删除子句。
需要仔细考虑如何以允许以后更改的方式表示近似值。 如果我们从 int 变为 int9,我们不想不得不扔掉所有东西。 应该可以使近似值“增长”或“缩小”。
我们应用于整数的所有操作都需要能够处理不断变化的位数。 例如,整数加法是根据 行波进位加法器 (ripple-carry adders) 建模的。 它在布尔方程中的子句需要以巧妙的方式使用假设。
我需要花更多的时间思考这将如何工作。
如果我们提前知道近似值将_如何_变化,甚至可能会提高效率。 如果它们只增长,并且每次精确地增长两位,那么也许有一种更有效的方式来构造这些方程。 我不确定。
NP 难问题 (NP-hard problems)
关于增量性的最后一个想法是,它将使 Sentient 达到能够解决 NP 难 (NP-hard) 问题的高度。 目前,Sentient 无法解决优化问题。 它没有专门搜索_最小值_或_最大值_。
但是,你可以通过多次运行相同的程序来_有效_地做到这一点。 例如,假设你想找到两个加起来等于 10 的数字,使它们的平方和最小化。 你可以编写如下程序:
这不是一个 NP 难问题,因为它可以用线性代数解决,但它证明了这一点。
int a, b, max;sum = a.square + b.square;invariant a + b == 10;invariant sum < max;expose a, b, sum, max;
▲ 使用 Sentient 解决优化问题
更现实的优化问题是 旅行商问题 (Travelling Salesman) 或 背包问题 (Knapsack) 。
然后,你可以多次运行它,减少 max 直到没有解决方案:
这找到了最佳解决方案 { a: 5, b: 5 },其平方和为 50,这是最小的。
视频略有加速。
我不确定我对近似值的定义是否扩展到优化问题,但肯定有机会以多种有用的方式使用增量性。
图灵完备性 (Turing-completeness)
当我们讨论 NP 难问题时,可能值得说几句关于可计算性和图灵完备性的话。 在 Sentient 网站 上,我写道:
事实上,Sentient 不是图灵完备的。 它是一种 Total 编程语言 – 它是完全可判定的,并且不会遇到停机问题。 这大大限制了它可以做的事情。 例如,不支持递归函数调用,并且永远不会支持。
永远不要说永不!
事实上,通过近似值的视角,Sentient 可能成为图灵完备的。 目前,Sentient 不支持递归函数调用:
int a;function factorial (n) {return n > 0 ? n * factorial(n - 1) : 1;};invariant a.factorial > 150;expose a;
▲ 一个假设的 Sentient 程序,使用递归
最小的解决方案是 { a: 6 },因为 6! = 720 > 150。
递归函数调用可以通过限制其递归深度来近似。 例如,如果 factorial 的近似深度为 5(或更小),它将找不到解决方案,但将其提高到 6 将会找到解决方案。 同样,你现在无法做到这一点:
int a;sum = 0;a.times(function^ () { sum += 3;});invariant sum > 10;expose a;
▲ 另一个不允许的假设程序
#times 方法调用函数 a 次。 它是从 Ruby 借来的。
^ 修饰符允许函数访问在外部定义的变量。
当你尝试运行此程序时,Sentient 会抛出一个错误:
使用
a调用times,但times仅支持整数文字 (arg #0)
不支持这样做,因为 a 是“符号化的”。 Sentient 无法将此程序编译为布尔方程,因为无法确定该方程的大小。 它的结构不是固定的。 #times 方法仅适用于“整数文字”,例如 5。
这是 Sentient 区分“符号化”变量和“字面”变量的几个地方之一。
同样,我们可以通过限制 a 的值来用近似值解决这个问题。
循环展开 (Loop unrolling)
这种技术已经以各种形式使用。 编译器经常出于性能原因展开循环和递归函数调用。 模型检查器 (Model checkers) 执行静态分析以检查不变量,通常使用 霍尔逻辑 (Hoare logic) 中建立的技术。
我很幸运能够在一次会议上见到 Tony Hoare,我在 这个播客 的第 12 集中谈到了这一点。
我认为循环展开是另一种近似。 可以通过静态分析来识别递归函数,并且外部程序可以决定当前搜索实例允许多少次调用。
从理论上讲,这些技术将允许 Sentient 在某种意义上成为图灵完备的。 这与增量 SAT 结合起来可以形成一个非常强大的系统。 能够解决与任意图灵机相关的问题将是惊人的。
我在 这个项目 中对此进行了一些探索,该项目根据 Cook-Levin 定理 (Cook-Levin theorem) 将图灵机简化为 SAT 。
下一步是什么?(Where next?)
我不确定。 我想更多地尝试这些想法,也许有一天将它们融入到 Sentient 或其他东西中。 增量性和接口设计显然存在挑战,但我认为我走在了正确的轨道上。
这是我写的第一篇关于 Sentient 和约束求解的深入文章,但希望会有更多。 如果你想了解更多信息,我将在 Twitter 上发布未来的更新。 感谢关注。