Doing the Prospero-Challenge in RPython
在 RPython 中完成 Prospero 挑战
CF Bolz-Tereick 2025-04-09 15:07 评论
最近我玩 Matt Keeter 的 Prospero Challenge 感到非常有趣。这个挑战是渲染莎士比亚《暴风雨》中的一句引言的 1024x1024 图像。输入是一个包含 7866 个操作的数学公式,每个像素都要计算一次。
对我个人而言,这个挑战特别吸引人的是,这个公式基本上是 SSA-form 中的一个轨迹——一个操作的线性序列,其中每个变量只被赋值一次。挑战在于尽可能快地评估这个公式。我尝试了许多加速执行的想法,并将在本篇有些漫无边际的文章中讨论它们。其中大部分内容与 Matt 的实现 Fidget 非常相似。有两个不同之处:
- 我尝试添加更多的窥孔优化,但它们最终并没有太大帮助。
- 我实现了一个“需求信息”优化,通过仅保留结果的符号来删除许多操作。这个优化最终是有用的。
这篇文章中的大部分原型设计都是在 RPython(Python2 的静态类型子集,可以编译成 C)中完成的,但我后来用 C 重写了程序以获得更好的性能。所有代码都可以在 GitHub 上找到。
输入程序
输入程序是一个操作序列,如下所示:
_0const2.95
_1var-x
_2const8.13008
_3mul_1_2
_4add_0_3
_5const3.675
_6add_5_3
_7neg_6
_8max_4_7
...
第一列是结果变量的名称,第二列是操作,其余的是操作的参数。var-x 是一个特殊操作,它返回正在渲染的像素的 x 坐标,var-y 类似,返回 y 坐标。结果的符号给出像素的颜色,绝对值并不重要。
一个基准解释器
为了运行程序,我首先解析它们并将寄存器名称替换为索引,以避免运行时进行任何字典查找。然后,我为 SSA-form 输入程序实现了一个简单的解释器。该解释器是一个简单的寄存器机器,其中每个操作按顺序执行。操作的结果存储到结果列表中,然后执行下一个操作。这是解释器的慢速基准实现,但对于与优化版本进行比较非常有用。
以下是代码的大致样子:
classDirectFrame(object):
def__init__(self, program):
self.program = program
self.next = None
defrun_floats(self, x, y, z):
self.setxyz(x, y, z)
return self.run()
defsetxyz(self, x, y, z):
self.x = x
self.y = y
self.z = z
defrun(self):
program = self.program
num_ops = program.num_operations()
floatvalues = [0.0] * num_ops
for op in range(num_ops):
func, arg0, arg1 = program.get_func_and_args(op)
if func == OPS.const:
floatvalues[op] = program.consts[arg0]
continue
farg0 = floatvalues[arg0]
farg1 = floatvalues[arg1]
if func == OPS.var_x:
res = self.x
elif func == OPS.var_y:
res = self.y
elif func == OPS.var_z:
res = self.z
elif func == OPS.add:
res = self.add(farg0, farg1)
elif func == OPS.sub:
res = self.sub(farg0, farg1)
elif func == OPS.mul:
res = self.mul(farg0, farg1)
elif func == OPS.max:
res = self.max(farg0, farg1)
elif func == OPS.min:
res = self.min(farg0, farg1)
elif func == OPS.square:
res = self.square(farg0)
elif func == OPS.sqrt:
res = self.sqrt(farg0)
elif func == OPS.exp:
res = self.exp(farg0)
elif func == OPS.neg:
res = self.neg(farg0)
elif func == OPS.abs:
res = self.abs(farg0)
else:
assert 0
floatvalues[op] = res
return self.floatvalues[num_ops - 1]
defadd(self, arg0, arg1):
return arg0 + arg1
defsub(self, arg0, arg1):
return arg0 - arg1
defmul(self, arg0, arg1):
return arg0 * arg1
defmax(self, arg0, arg1):
return max(arg0, arg1)
defmin(self, arg0, arg1):
return min(arg0, arg1)
defsquare(self, arg0):
val = arg0
return val*val
defsqrt(self, arg0):
return math.sqrt(arg0)
defexp(self, arg0):
return math.exp(arg0)
defneg(self, arg0):
return -arg0
defabs(self, arg0):
return abs(arg0)
在 prospero 图像文件上运行朴素的解释器非常慢,因为它执行 7866 * 1024 * 1024 次浮点运算,加上解释开销。
使用四叉树渲染图片
Matt 在他非常精彩的 演讲 中描述的方法是使用 四叉树:将图像递归地细分为象限,并在每个象限中评估公式。对于每个象限,您可以通过进行范围分析来简化公式。经过几个递归步骤后,公式会变得明显更小,通常只有几百或几十个操作。
在递归的底部,您要么到达一个范围分析显示所有像素的符号都已确定的正方形,然后您可以填充象限的所有像素。或者,您可以执行每个像素来评估象限中的(现在简单得多的)公式。
这是 JIT 编译器/优化技术的一个有趣的用例,需要优化器本身执行得非常快,因为它对于算法的性能至关重要。优化器运行数百次以渲染单个图像。如果该算法用于 3D 模型,则它变得更加重要。
编写一个简单的优化器
实现四叉树递归很简单。由于程序没有控制流,因此优化器很容易编写。我写了几篇关于如何轻松为线性操作序列编写优化器的博客文章,并且我正在使用这些 Toy Optimizer 文章中描述的方法。区间分析基本上是操作的 抽象解释。优化器对输入程序进行顺序正向传递。对于每个操作,计算输出区间。优化器还基于计算的区间执行优化,这有助于减少执行的操作数量(我将在稍后进一步讨论)。
这是进行优化的 Python 代码的草图:
classOptimizer(object):
def__init__(self, program):
self.program = program
num_operations = program.num_operations()
self.resultops = ProgramBuilder(num_operations)
self.intervalframe = IntervalFrame(self.program)
# old index -> new index
self.opreplacements = [0] * num_operations
self.index = 0
defget_replacement(self, op):
return self.opreplacements[op]
defnewop(self, func, arg0=0, arg1=0):
return self.resultops.add_op(func, arg0, arg1)
defnewconst(self, value):
const = self.resultops.add_const(value)
self.intervalframe.minvalues[const] = value
self.intervalframe.maxvalues[const] = value
#self.seen_consts[value] = const
return const
defoptimize(self, a, b, c, d, e, f):
program = self.program
self.intervalframe.setxyz(a, b, c, d, e, f)
numops = program.num_operations()
for index in range(numops):
newop = self._optimize_op(index)
self.opreplacements[index] = newop
return self.opreplacements[numops - 1]
def_optimize_op(self, op):
program = self.program
intervalframe = self.intervalframe
func, arg0, arg1 = program.get_func_and_args(op)
assert arg0 >= 0
assert arg1 >= 0
if func == OPS.var_x:
minimum = intervalframe.minx
maximum = intervalframe.maxx
return self.opt_default(OPS.var_x, minimum, maximum)
if func == OPS.var_y:
minimum = intervalframe.miny
maximum = intervalframe.maxy
return self.opt_default(OPS.var_y, minimum, maximum)
if func == OPS.var_z:
minimum = intervalframe.minz
maximum = intervalframe.maxz
return self.opt_default(OPS.var_z, minimum, maximum)
if func == OPS.const:
const = program.consts[arg0]
return self.newconst(const)
arg0 = self.get_replacement(arg0)
arg1 = self.get_replacement(arg1)
assert arg0 >= 0
assert arg1 >= 0
arg0minimum = intervalframe.minvalues[arg0]
arg0maximum = intervalframe.maxvalues[arg0]
arg1minimum = intervalframe.minvalues[arg1]
arg1maximum = intervalframe.maxvalues[arg1]
if func == OPS.neg:
return self.opt_neg(arg0, arg0minimum, arg0maximum)
if func == OPS.min:
return self.opt_min(arg0, arg1, arg0minimum, arg0maximum, arg1minimum, arg1maximum)
...
defopt_default(self, func, minimum, maximum, arg0=0, arg1=0):
self.intervalframe._set(newop, minimum, maximum)
return newop
defopt_neg(self, arg0, arg0minimum, arg0maximum):
# peephole rules go here, see below
minimum, maximum = self.intervalframe._neg(arg0minimum, arg0maximum)
return self.opt_default(OPS.neg, minimum, maximum, arg0)
@symmetric
defopt_min(self, arg0, arg1, arg0minimum, arg0maximum, arg1minimum, arg1maximum):
# peephole rules go here, see below
minimum, maximum = self.intervalframe._max(arg0minimum, arg0maximum, arg1minimum, arg1maximum)
return self.opt_default(OPS.max, minimum, maximum, arg0, arg1)
...
然后,在四叉树递归的底部简单地解释生成的优化轨迹。 Matt 还谈到了从它们生成机器代码,但是当我尝试使用 PyPy 的 JIT 来执行此操作时,它在生成机器代码方面太慢了。
测试区间抽象域的可靠性
为了确保我在优化器中的区间计算是正确的,我实现了一个基于假设的基于属性的测试。它检查区间域的抽象转换函数的可靠性。它通过为操作生成随机具体输入值和围绕随机具体值的随机区间来实现此目的,然后执行具体操作以获得具体输出,最后检查应用于输入区间的抽象转换函数是否给出包含具体输出的区间。
例如,square 操作的随机测试如下所示:
fromhypothesisimport given, strategies, assume
frompyfidget.vmimport IntervalFrame, DirectFrame
importmath
regular_floats = strategies.floats(allow_nan=False, allow_infinity=False)
defmake_range_and_contained_float(a, b, c):
a, b, c, = sorted([a, b, c])
return a, b, c
frame = DirectFrame(None)
intervalframe = IntervalFrame(None)
range_and_contained_float = strategies.builds(make_range_and_contained_float, regular_floats, regular_floats, regular_floats)
defcontains(res, rmin, rmax):
if math.isnan(rmin) or math.isnan(rmax):
return True
return rmin <= res <= rmax
@given(range_and_contained_float)
deftest_square(val):
a, b, c = val
rmin, rmax = intervalframe._square(a, c)
res = frame.square(b)
assert contains(res, rmin, rmax)
此测试生成一个随机浮点数 b,以及另外两个浮点数 a 和 c,以使区间 [a, c] 包含 b。然后,该测试检查 b 上的 square 操作的结果是否包含在 square 操作的抽象转换函数返回的区间 [rmin, rmax] 中。
窥孔重写
Matt 在他的实现中唯一做的优化是一个窥孔优化规则,它删除了参数区间不重叠的 min 和 max 操作。在这种情况下,优化器可以静态地知道哪个参数将是操作的结果。我在我的实现中也实现了这种窥孔优化,但我也添加了一些我认为有用的窥孔优化。
classOptimizer(object):
defopt_neg(self, arg0, arg0minimum, arg0maximum):
# new: add peephole rule --x => x
func, arg0arg0, _ = self.resultops.get_func_and_args(arg0)
if func == OPS.neg:
return arg0arg0
minimum, maximum = self.intervalframe._neg(arg0minimum, arg0maximum)
return self.opt_default(OPS.neg, minimum, maximum, arg0)
@symmetric
defopt_min(self, arg0, arg1, arg0minimum, arg0maximum, arg1minimum, arg1maximum):
# Matt's peephole rule
if arg0maximum < arg1minimum:
return arg0 # we can use the intervals to decide which argument will be returned
# new one by me: min(x, x) => x
if arg0 == arg1:
return arg0
func, arg0arg0, arg0arg1 = self.resultops.get_func_and_args(arg0)
minimum, maximum = self.intervalframe._max(arg0minimum, arg0maximum, arg1minimum, arg1maximum)
return self.opt_default(OPS.max, minimum, maximum, arg0, arg1)
...
但是,事实证明,我尝试添加其他窥孔优化规则的所有尝试都不是很有用。大多数规则从未触发,而触发的规则仅对程序的性能产生了很小的影响。我发现唯一有用的窥孔优化是 Matt 在他的演讲中描述的窥孔优化。对于 prospero.vm 输入,Matt 的 min / max 优化是我的窥孔优化器应用的所有重写的 96%。剩余的 4% 的重写是(百分比是那 4% 的):
--x => x 4.65%
(-x)**2 => x ** 2 0.99%
min(x, x) => x 20.86%
min(x, min(x, y)) => min(x, y) 52.87%
max(x, x) => x 16.40%
max(x, max(x, y)) => max(x, y) 4.23%
最后,事实证明,拥有这些额外的优化规则使系统的总运行时间上升了。检查重写并非没有成本,并且由于它们很少应用,因此它们无法通过提高性能来支付自己的成本。
我尝试过的一些其他规则根本没有触发:
a * 0 => 0
a * 1 => a
a * a => a ** 2
a * -1 => -a
a + 0 => a
a - 0 => a
x - x => 0
abs(known positive number x) => x
abs(known negative number x) => -x
abs(-x) => abs(x)
(-x) ** 2 => x ** 2
如果这是一个真正严肃的实现,那么这种调查显然过于关注单个程序,应该使用更大的示例输入集来重新进行。
需求信息优化
LLVM 有一个名为“demanded bits”的静态分析通道。它是一个向后分析,允许您确定值的哪些位实际上在最终结果中使用。然后,此信息可用于窥孔优化。例如,如果您有一个表达式来计算一个值,但只有该值的最后一个字节在最终结果中使用,则可以优化该表达式以仅计算最后一个字节。
这是一个例子。假设我们首先字节交换一个 64 位整数,然后屏蔽掉最后一个字节:
uint64_tbyteswap_then_mask(uint64_ta){
returnbyteswap(a)&0xff;
}
在这种情况下,byteswap(a) 表达式的“需求位”是 0b0...011111111,这反过来说明我们不关心上面的 56 位。因此,整个表达式可以优化为 a >> 56。
对于 Prospero 挑战,我们可以观察到,对于生成的像素值,根本不使用结果的值,而只使用它的符号。本质上,每个程序都隐含地以一个 sign 操作结束,该操作为负值返回 0.0,为正值返回 1.0。为了清楚起见,我将在本节的其余部分显示此 sign 操作,即使它实际上不在真实代码中。
这使得进一步简化某些 min/max 操作成为可能。这是一个程序示例,以及变量的区间:
xvar-x# [0.1, 1]
yvar-y# [-1, 1]
mminxy# [-1, 1]
outsignm
这个程序可以优化为:
yvar-y
outsignm
因为该表达式与原始表达式具有相同的结果:如果 x > 0.1,则 min(x, y) 的结果要为负数,则 y 需要为负数。
另一个更复杂的例子是:
xvar-x# [1, 100]
yvar-y# [-10, 10]
zvar-z# [-100, 100]
m1minxy# [-10, 10]
m2maxzout# [-10, 100]
outsignm2
可以优化为:
yvar-y
zvar-z
m2maxzy
outsignm2
这是因为如果 x > 0,则 min(x, y) 的符号与 y 的符号相同,因此 max(z, min(x, y)) 的符号与 max(z, y) 的符号相同。
为了实现这种优化,我在窥孔优化正向传递之后对程序进行向后传递。对于我遇到的每一个 min 调用,其中一个参数是正的,我可以优化掉 min 调用,并用另一个参数替换它。对于 max 调用,我递归地简化它们的参数。
代码大致如下所示:
defwork_backwards(resultops, result, minvalues, maxvalues):
defdemand_sign_simplify(op):
func, arg0, arg1 = resultops.get_func_and_args(op)
if func == OPS.max:
narg0 = demand_sign_simplify(arg0)
if narg0 != arg0:
resultops.setarg(op, 0, narg0)
narg1 = demand_sign_simplify(arg1)
if narg1 != arg1:
resultops.setarg(op, 1, narg1)
if func == OPS.min:
if minvalues[arg0] > 0.0:
return demand_sign_simplify(arg1)
if minvalues[arg1] > 0.0:
return demand_sign_simplify(arg0)
narg0 = demand_sign_simplify(arg0)
if narg0 != arg0:
resultops.setarg(op, 1, narg0)
narg1 = demand_sign_simplify(arg1)
if narg1 != arg1:
resultops.setarg(op, 1, narg1)
return op
return demand_sign_simplify(result)
在我的实验中,这种优化使我可以在八叉树的各个级别删除 prospero 中 25% 的操作。我将在稍后简要介绍性能结果。
关于需求符号简化的进一步想法
还有另一种想法是如何对表达式的评估进行短路,我简要尝试过但没有坚持到底。让我们回到上一小节的第一个示例,但使用不同的区间:
xvar-x# [-1, 1]
yvar-y# [-1, 1]
mminxy# [-1, 1]
outsignm
现在我们不能在优化器中使用“需求符号”技巧,因为 x 和 y 都不是已知的正数。但是,在程序_执行_期间,如果 x 结果为负数,我们可以立即结束此轨迹的执行,因为我们知道结果必须为负数。
因此,我尝试将 return_early_if_neg 标志添加到具有此属性的所有操作。然后,解释器检查是否在操作上设置了该标志,如果结果为负数,则提前停止程序的执行:
xvar-x[return_early_if_neg]
yvar-y[return_early_if_neg]
mminxy
outsignm
这看起来很有希望,但这也是一种权衡,因为检查标志和值的成本并不为零。这是对解释器的更改的草图:
classDirectFrame(object):
...
defrun(self):
program = self.program
num_ops = program.num_operations()
floatvalues = [0.0] * num_ops
for op in range(num_ops):
...
if func == OPS.var_x:
res = self.x
...
else:
assert 0
if program.get_flags(op) & OPS.should_return_if_neg and res < 0.0:
return res
floatvalues[op] = res
return self.floatvalues[num_ops - 1]
我在 RPython 版本中实现了这一点,但最终没有将其移植到 C,因为它会干扰 SIMD。
死代码消除
Matt 通过对程序进行单个向后传递来执行死代码消除。这是一个非常简单有效的优化,我也在我的实现中实现了它。死代码消除传递非常简单:它首先将结果操作标记为已使用。然后,它向后遍历程序。如果当前操作已使用,则其参数也被标记为已使用。之后,从程序中删除所有未标记为已使用的操作。PyPy JIT 实际上以完全相同的方式对轨迹执行死代码消除(并且我认为我们从未在博客上解释过它是如何工作的),因此我认为值得一提。
Matt 还将寄存器分配作为向后传递的一部分执行,但我没有实现它,因为我对这方面不太感兴趣。
优化器的随机测试
为了确保我没有破坏优化器中的任何内容,我实现了一个测试,该测试生成随机输入程序并检查优化器的输出是否等效于输入程序。该测试生成随机操作,操作的随机区间以及该区间内的随机输入值。然后,它在输入程序上运行优化器,并检查输出程序是否与输入程序具有相同的结果。这又是使用 hypothesis 实现的。Hypothesis 的测试用例最小化功能对于查找优化器错误非常有用。分析一个包含数千个操作的输入文件的问题并不有趣,但 Hypothesis 经常生成仅包含几个操作的简化测试用例。
可视化程序
实际上,很好地可视化 prospero.vm 是非常令人烦恼的,因为它太大而无法将其直接馈送到 Graphviz 中。通过将几个操作组合在一起,我使问题稍微容易了一些,其中只有组中的第一个操作被用作程序中进一步的多个操作的参数。这使得 Graphviz 稍微易于管理。但是,它仍然没有足够的改进来能够以其在八叉树顶部的未优化形式可视化所有 prospero.vm。
这是八叉树级别之一的优化 prospero.vm 的可视化:
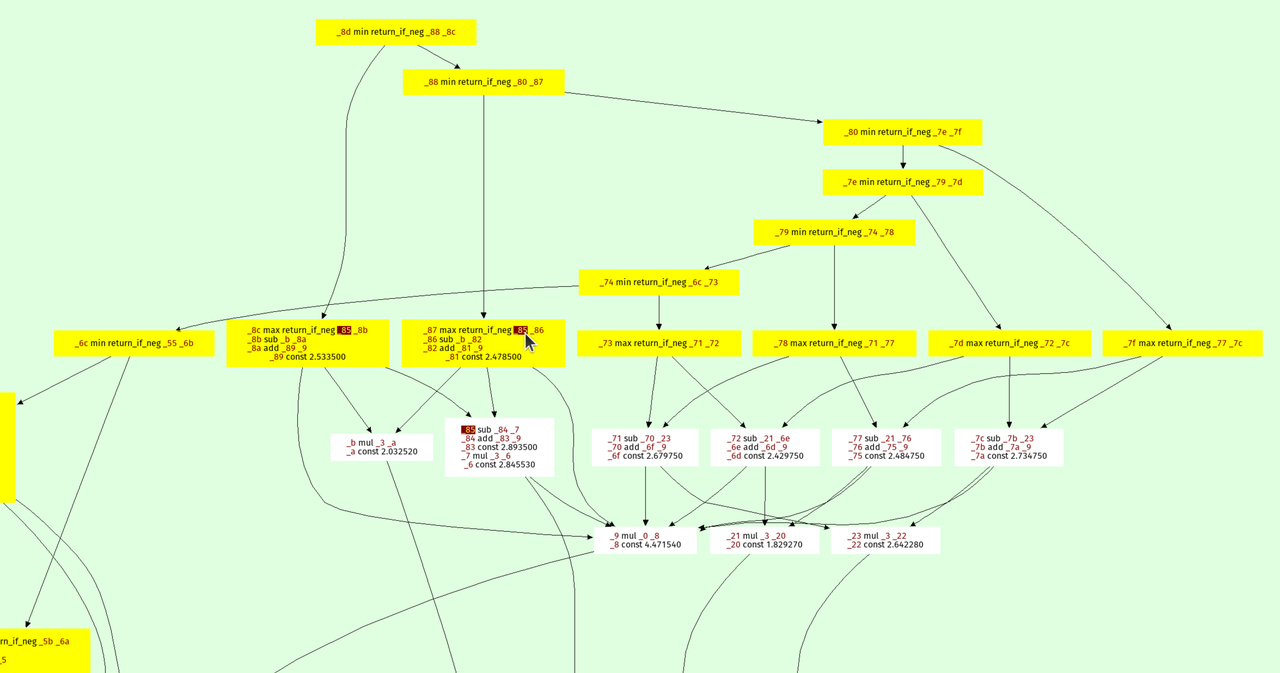
结果位于顶部,每个节点指向其参数。 min 和 max 操作形成了表达式树的一种“脊柱”,因为它们在构造实体几何意义上是并集和交集。
我还编写了一个函数来可视化八叉树递归本身,输出如下所示:

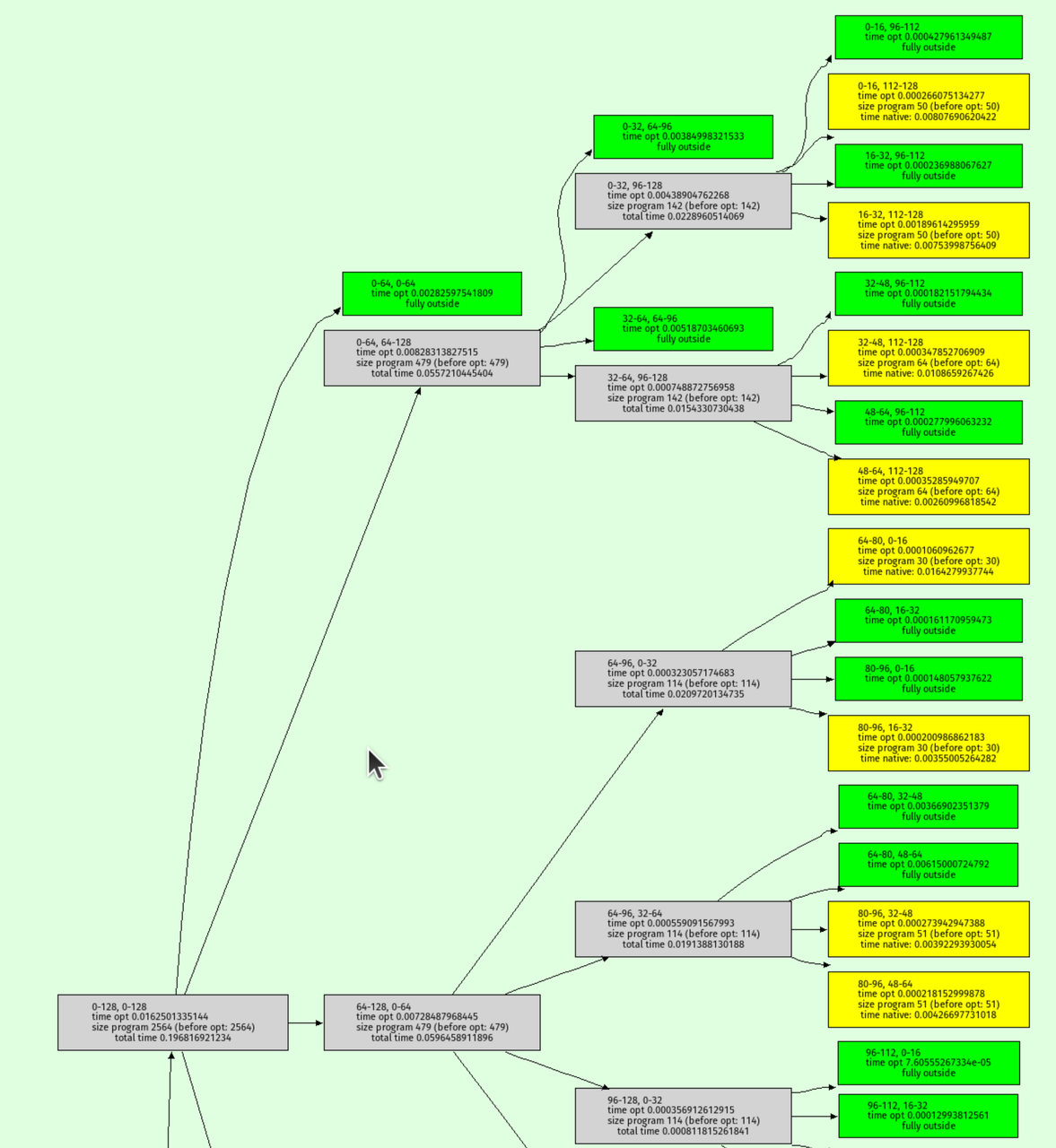
绿色节点是区间分析确定输出必须完全在形状之外的地方。黄色节点是八叉树递归到底的地方。
C 实现
为了实现更快的性能,我决定用 C 重写实现。虽然 RPython 非常适合原型设计,但控制代码的底层方面可能具有挑战性。在 C 中重写使我可以尝试我一直很好奇的几种技术:
- 用于解释器的
musttail优化。 - SIMD (Single Instruction, Multiple Data): 使用 Clang 的
ext_vector_type,我一次处理八个像素,使用 AVX(或其他一些我不完全理解的 SIMD 魔法)。 - 有效的结构体打包:我将操作结构体打包成仅 8 个字节,方法是将操作的最大数量限制为 65,536,目的是使优化器更快。
我没有严格研究每种技术的性能影响,因此其中一些技术可能没有显着贡献。但是,重写对我来说是一次有趣的探索这些技术的练习。代码可以在 此处 找到。
测试 C 实现
在各个时间点,我的 C 实现中都存在错误,导致出现了一个有趣的、充满故障的 Prospero 版本:

为了找到这些错误,我使用了与 RPython 版本中相同的随机测试方法。我以 Python 字符串的形式生成随机输入程序,并检查 C 实现的输出是否等效于 RPython 实现的输出(只需调用 shell 并读取生成的图像,然后比较像素)。这有助于确保 C 实现正确并且没有引入任何错误。要做到这一点非常棘手,原因是我没有想到。它们中的很多都与我在 C 中使用 float 而 Python 使用 double 作为其(Python)float 类型有关。这使得随机测试仪找到了奇怪的浮点数极端情况,其中宽度之间的舍入行为不同。
我通过在运行随机测试时使用 IFDEF 在 C 中使用 double 解决了这些问题。
观看随机程序生成器生成随机图像非常有趣,以下是一些:
性能
以下是我的笔记本电脑(一台配备 32 GiB RAM 并在 Ubuntu 24.04 上运行的 AMD Ryzen 7 PRO 7840U)上的一些非常粗略的性能结果,比较了 RPython 版本、C 版本(带和不带需求信息)以及 Fidget(在 vm 模式下,它的 JIT 对我来说更糟),对于 1024x1024 和 4096x4096 图像:
| 实现 | 1024x1024 | 4096x4096 | | --------------------- | -------- | -------- | | RPython | 26.8ms | 75.0ms | | C (无需求信息) | 24.5ms | 45.0ms | | C (需求信息) | 18.0ms | 37.0ms | | Fidget | 10.8ms | 57.8ms |
需求信息似乎有很大帮助,这很高兴看到。
结论
就是这样!我从这个挑战中获得了许多乐趣,并且还有很多其他想法想要尝试,感谢 Matt 提出了这个有趣的难题。
评论
PyPy 博客文章
通过向 源代码存储库 发起 PR 来创建访客帖子
近期文章
- 在 RPython 中完成 Prospero 挑战
- PyPy v7.3.19 发布
- 在 PyPy 的 GC 中使用 VMProf 进行低开销分配采样
- PyPy v7.3.18 发布
- PyPy 中跟踪的思考
- 迈向 PyPy3.11 - 更新
- 访客帖子:RPython 解释器中的最终编码
- PyPy JIT 中整数运算的窥孔转换规则的 DSL
- 访客帖子:PortaOne 如何使用 PyPy 进行高性能处理,每月连接超过 10 亿次电话
- PyPy v7.3.17 发布