骰子与队列:使用模拟理解 Queuing Theory
骰子与队列
Feb 25, 2025
介绍
Queuing Theory 的一个关键见解是,对于无界系统,随着利用率接近 100%,平均队列长度会显著增加。理论模型显示这种增长没有上限,并且在 100% 利用率时,产生的平均队列长度趋向于无穷大。这一点很重要,因为队列本身会消耗资源,无论是计算机上的内存或磁盘空间,还是工厂中的车间空间。在一个理想的世界里,我们不需要队列。毕竟,谁喜欢排队呢?只有当队列中项目的到达率小于或等于离开率,并且两者都没有变化时,这才是可能的。这在现实世界中不太可能发生。
队列模型通常使用 Kendall Notation (例如 M/M/1 或 M/D/1) 来表示。这些模型指定了不同的到达和离开分布,例如 Poisson 或 Deterministic。它们最终会有封闭形式的表达式,将平均队列长度定义为不同系统参数的函数。虽然这些公式相当容易使用,但我希望对这些模型的行为有更直观的理解,并决定构建一个基于多次掷骰子想法的模拟。
理论与模拟设置
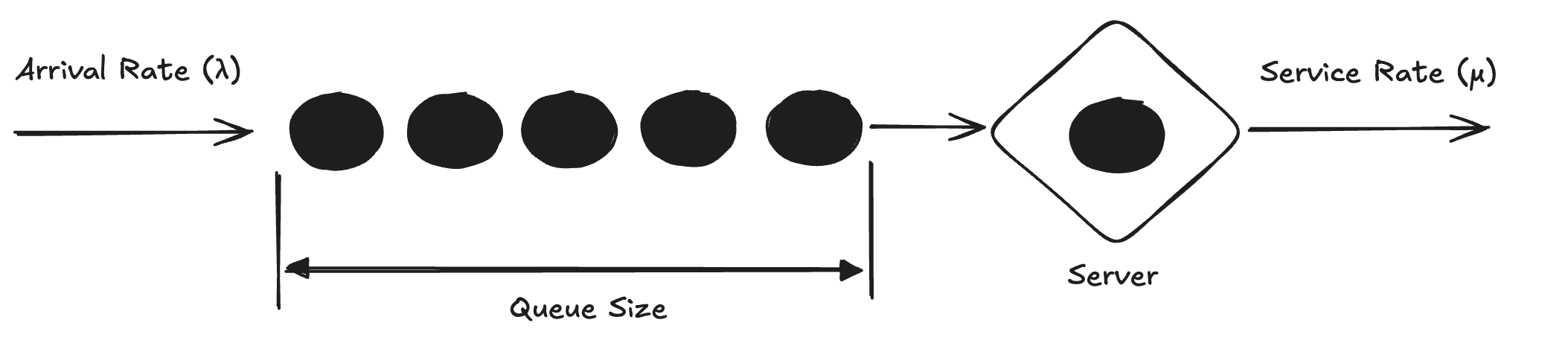
队列很容易可视化。在下图中,我们有一个包含 5 个项目的队列,以及 1 个正在被服务的项目。这是一个先进先出 (FIFO) 队列,因此当一个项目到达时,它必须等待排在它前面的所有项目都被服务完才能离开队列。在标有“server”的块中也有一个项目。此项目不在队列中,但仍被视为“系统”的一部分。因此,在我们的示例中,我们的队列大小为 5,系统中共有 6 个项目。
到达率 (λ) 是项目进入队列的平均速率。服务或离开率 (μ) 是项目离开队列的平均速率。这两个速率都以单位时间内的项目数表示(例如,10 个项目/分钟)。很容易推断,如果到达率超过离开率,队列大小将随着时间推移而增加。同样,如果到达率低于离开率,队列大小将随着时间推移而减小。有趣的是,当像许多现实世界系统中那样,平均值周围存在变化时,队列的行为方式。
在分析队列系统行为时,利用率 (ρ) 是一个有用的指标。这有助于估计 server 繁忙的时间百分比。
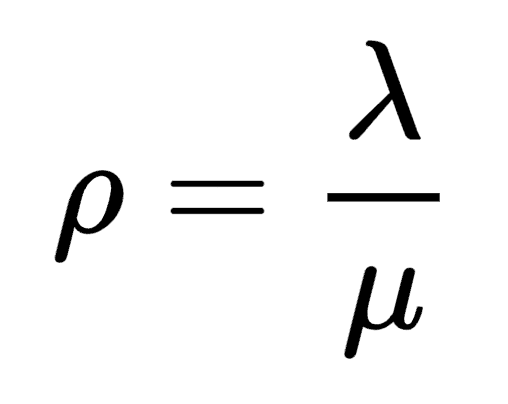
理论和经验证据表明,当利用率趋于 0 时,平均队列大小也趋于 0。但是,随着利用率接近 1,队列大小会显着增加。如果利用率大于 1,则意味着平均到达率大于服务率,并且队列将持续无限增长。
为了更好地理解这些动态,让我们考虑一个实验,我们将一分钟分成 60 秒,并在每秒掷一个 6 面骰子。如果骰子落在 6 上,我们将计数记录到我们的笔记本中。在一分钟结束时,我们将所有计数加起来。这将是我们在给定分钟内队列中的项目到达数量。这里的想法是,所有到达的可能性均等,并且它们彼此不依赖。
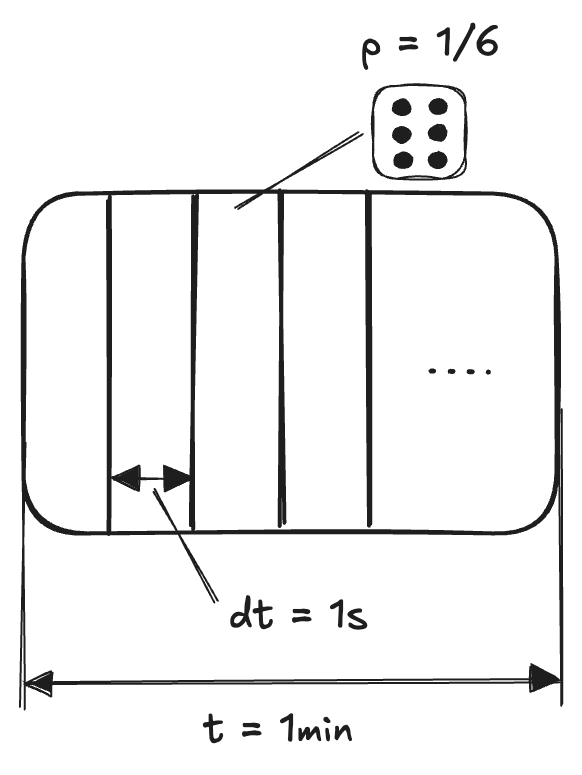
与其耗尽我们的手掷数百次骰子,我们可以编写一个 Python 函数 arrivals() 来模拟上述场景。请注意,每次掷骰子都有 1/6 的几率落在 6 上。我们可以使用 random() 函数,该函数返回 0 到 1 之间的均匀随机十进制值。每次它返回的值小于 1/6 时,我们都会增加计数。
def arrivals():
"""
This function simulates 60 roles of a die and
returns the number of times a single face
(e.g. 6) shows up. This simulates a binomial
distribution where the expected value is
E[X] = n * p = (1/6) * 60 = 10.
"""
p = 1 / 6 # chances of rolling a six
n = 60 # number of rolls
count = 0
for i in range(n):
if random.random() < p: count += 1
return count
所以我们现在有了一种随机生成到达的方法。对于服务率 (λ),我们可以保持简单并假设我们的 server 每分钟可以服务 10 个项目,且没有变化。下面的公式显示了队列每分钟的变化,其中队列大小的变化由 arrivals() 和服务率 λ 之间的差异决定。但是,由于没有负大小的队列,max() 函数有助于防止队列大小低于 0。
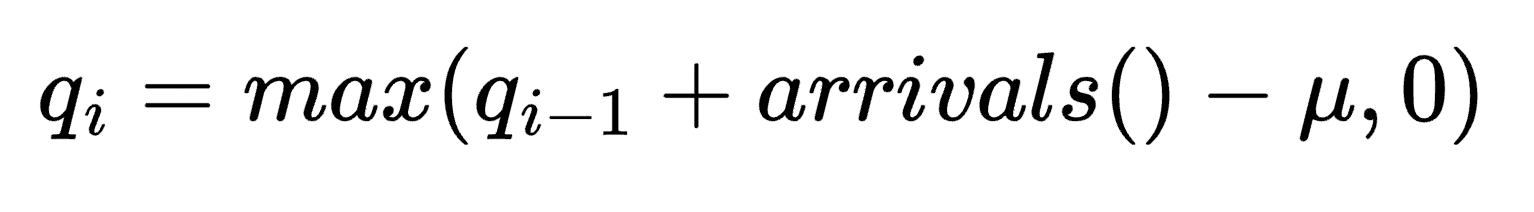
下表显示了运行如上所述的模拟获得的结果示例。arrivals() 函数每分钟运行一次,以获得已到达的新项目数。同时,server 服务并从队列中移除 10 个项目。例如,队列从大小为 0 开始。在第一分钟结束时,到达 11 个项目并处理 10 个项目,这使队列大小为 1。
请注意,到达的值分散在 10 左右。这是因为 6 面骰子掷 60 次最可能的结果是平均落在特定面上的次数为 10 次。我们看到的最大偏差是在第 8 分钟,当 6 的计数只有 5 时。
分钟 | 到达数 (6's) | 队列大小 ---|---|--- 1 | 11 | 1 2 | 7 | 0 3 | 8 | 0 4 | 13 | 3 5 | 8 | 1 6 | 12 | 3 7 | 8 | 1 8 | 5 | 0 9 | 10 | 0 10 | 7 | 0
我们上面模拟的是 Kendall Notation 中 M/D/1 队列的估计版本。M 代表 Markovian,表示到达过程遵循 Poisson 分布。有时这也称为“无记忆”到达过程。这实际上是我们在每分钟掷 60 次虚拟骰子并计算每次出现 6 的次数来近似的。每秒都是一次掷骰子,代表另一个项目可能到达队列的 1/6 的机会。每次掷骰子都是独立的,因此系统中没有“记忆”。这样做之所以有效,是因为以这种方式掷骰子并计算成功事件的数量是二项式分布的一种形式,对于大量的掷骰子,它近似于 Poisson 分布。M/D/1 中的“D”代表 deterministic,这意味着我们假设一个完美的 server,没有变化。其服务率是恒定的。最后,M/D/1 中的“1”表示我们只有一个 server。此形式的队列中项目的平均数量的理论解由下面的公式给出,该公式显示为利用率的函数。
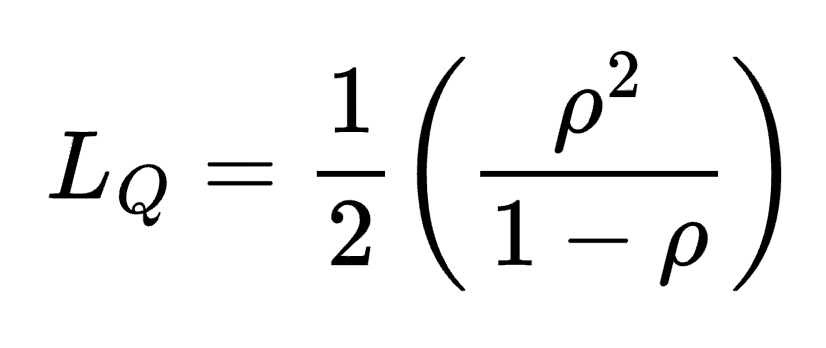
上面的等式仅适用于小于 1 的利用率。在该等式中,如果利用率为 0,则平均队列大小为 0,这很有意义,因为它对应于 0 到达或无限服务率。但是,我们可以看到,随着利用率接近 1,平均队列大小会增加。在利用率达到 1 的极限时,平均队列大小将变为无穷大。
结果及与理论的比较
我们已经开发了一个简单的 M/D/1 队列模拟。现在,让我们在不同的场景下运行此模拟 24 小时,并将一些平均队列大小结果与理论进行比较。在所有这些场景中,预期到达率将保持在 10 的值。只会改变服务率以显示不同的利用率。
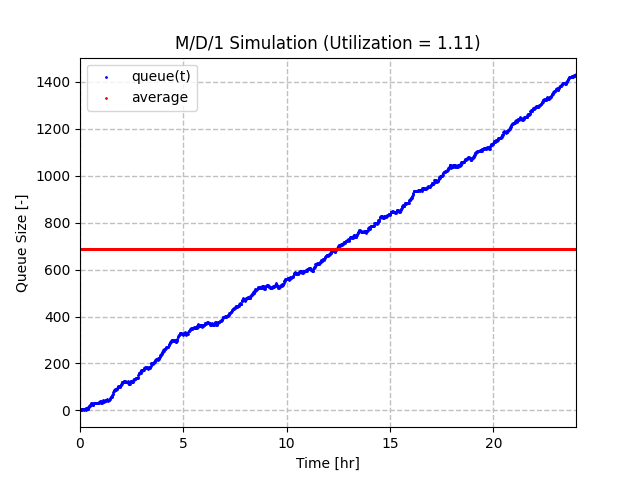
第一个示例是到达率为 10,服务率为 9,这使我们的利用率为 1.11。您可以看到队列从 0 增长到略高于 1400 个项目。由于预期速率每分钟相差 1 个项目,因此这很有意义,因为 24 小时内有 1440 分钟。随着队列由于到达量的自然变化而增加,也存在一些明显的噪声和变化。另请注意,平均队列大小约为 700,但如果允许模拟持续超过 24 小时,则该值将继续增加到无穷大。
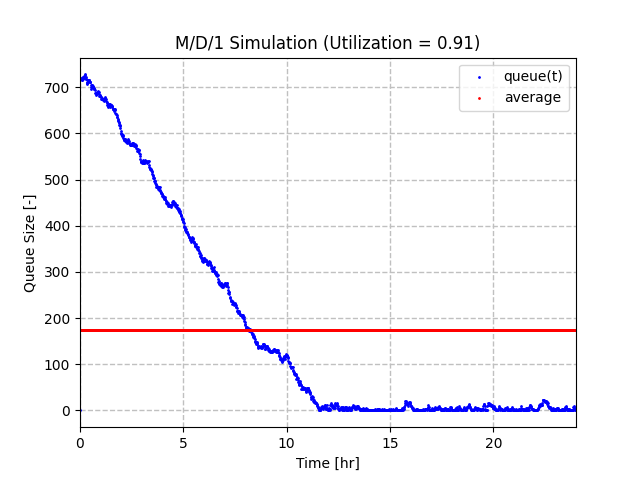
为了测试相反的情况,我们可以显示一个服务率为 11 且到达率为 10 的队列,这给出了 0.91 的利用率。该队列也被赋予了从 720 个项目开始的初始条件。您可以看到队列大小平均以每分钟 1 个项目的速率下降。之后,由于到达的变化,它往往会在 0 附近波动。这里的平均队列大小约为 175,这主要是由于队列从一个较大的值开始。
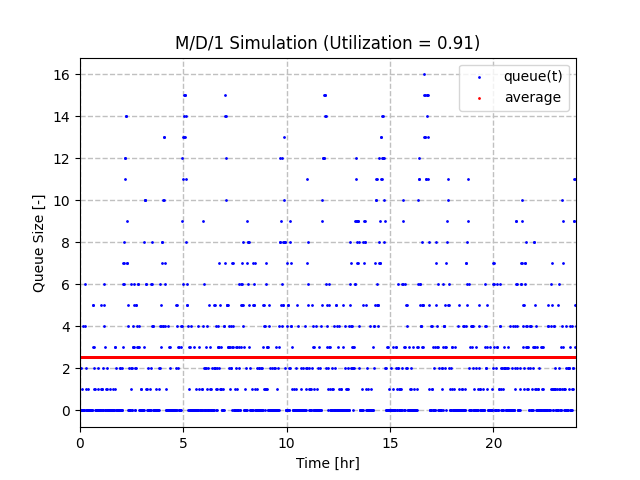
让我们看一下与最后一个场景相同的场景,但从队列大小为 0 开始。在利用率为 0.91 的情况下,我们看到的最大队列大小为 16。但是,平均值要低得多,为 2.5。这与 M/D/1 队列的理论平均队列大小为 4.6(利用率为 0.91)的量级相同。
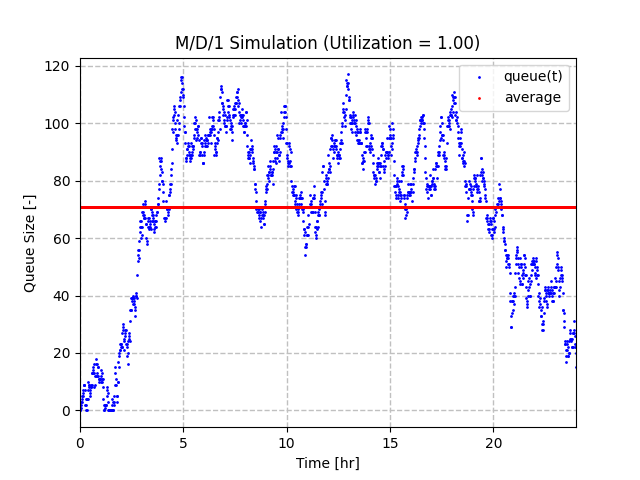
最后,我们可以看一下当利用率为 1.0 时的结果。在这里,队列大小增加到接近 120,平均大小约为 70。参考 M/D/1 队列的队列大小方程,我们预计此大小的平均队列的利用率为 0.993。因此,我们的模拟模型和封闭形式的方程之间存在一些细微的差异。话虽如此,该图表明,接近 100% 利用率的排队系统在队列大小方面存在很大波动。这是因为预期值是平衡的,并且队列是否会继续增加在很大程度上取决于运气。无论如何,在这种情况下,您都不能假设队列不会增加。
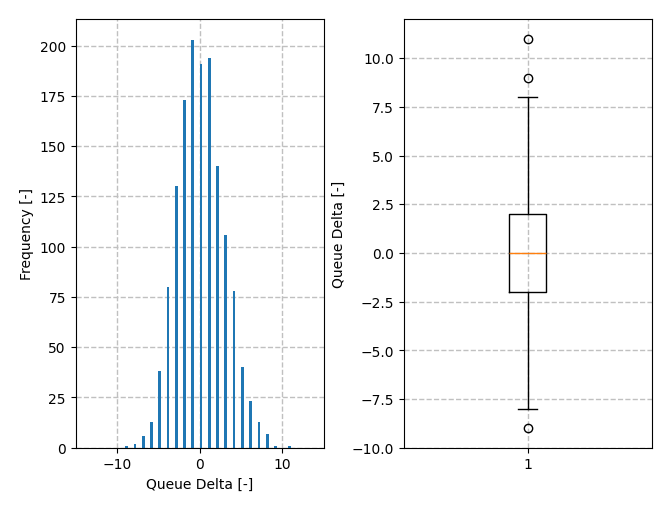
对于 100% 利用率的情况,有趣的是看一下整个 24 小时模拟中每分钟队列大小变化的分布。下面的直方图显示 deltas 主要集中在零附近。请注意,有一些大于 10 的长尾 deltas,因为可能会获得比 10 大得多的到达量(例如,60),但可能发生的最小到达量是 0。须状图和箱线图也显示了一些高端的异常值。从这些图表中并不明显,但是平均 delta 也略微为正。部分原因是如果队列大小小于 10,则 server 无法使用其全部容量。换句话说,队列不能具有负长度。
结论
我希望您从这个从掷骰子的角度对 Queuing Theory 进行的小型探索中有所收获。我的目标是提供一个更直观的示例,说明什么是遵循 Poisson 分布的到达过程。此外,查看这些队列的时序表示很有用,因为大多数等式都是针对某种形式稳定下来的系统的平均队列长度而提出的。我们看到,模拟在定性上确实与理论相符,因为平均队列大小往往会随着利用率接近 100% 而显着增加。有趣的是,由于队列不能为负数,因此几乎可以保证队列的平均大小,这仅仅是由于到达和离开的变化所致。
Justin Cartwright
In theory there is no difference between theory and practice. In practice there is. - Yogi Berra (in theory)