使用 Racket 编写我自己的图像抖动算法
Amanvir Parhar • 2025 年 2 月 9 日
现在，黑白图像似乎已经成为过去。在这样一个我们 постоянно被可以轻松显示 RGB 色彩空间中所有 1670 万种颜色的屏幕所包围的时代，不难理解为什么会这样。
那么，在 2025 年，为什么还有人关心黑白图像呢？
嗯，大概在一个多月前，我也会问同样的问题。但是，在今年一月，我制作了 Guten，这是一个依靠嵌入式热敏打印机在每天早上 7:00 推出我自己的定制报纸的设备。在构建这个有趣的小项目时，我意识到，如果我希望 Guten 打印出一张图像，它将需要只包含黑色和白色像素。
我很难接受这个现实……我该如何拍摄一张可爱的三通道猫的照片，并让我的打印机正确地打印出来呢？
本文介绍了解决我这个问题的方案：图像抖动。在此过程中，我还会尝试带您了解我在 Racket 编程语言中实现新的抖动算法的历程。
什么是图像抖动？
Image dithering 是一种技术，用于使用更小的调色板（在我们的例子中，是黑白）来表示依赖于大型调色板（例如 RGB）的图像，从而使人眼感知到新图像具有比实际更多的颜色深度。
这是一个泰姬陵的彩色照片和同一照片的抖动版本的并排比较：
为了正确理解抖动的工作原理，我们首先需要讨论灰度。
转换为灰度
在我们甚至开始研究我们的抖动算法之前，我们需要将我们色彩鲜艳的猫照片（我将在整个博客文章中使用它作为示例）转换为仅由白色、灰色和黑色组成的照片。
换句话说，我们需要将图像中的每个像素转换为红色、绿色和蓝色通道的值都相同的像素：
R = G = B
一种简单的方法是将任何给定像素设置为其三个 RGB 值的平均值：
(R + G + B) / 3
但是，我们也可以使用这个奇特的公式来执行转换，该公式根据每个 RGB 分量对颜色整体感知亮度的相对贡献来为其分配系数：
- 2126 * R + 0.7152 * G + 0.0722 * B
用 Racket 代码实现最后一个公式以将图像转换为灰度看起来像这样（注意 - 从此处开始显示的所有代码也可以在 GitHub 上找到）：
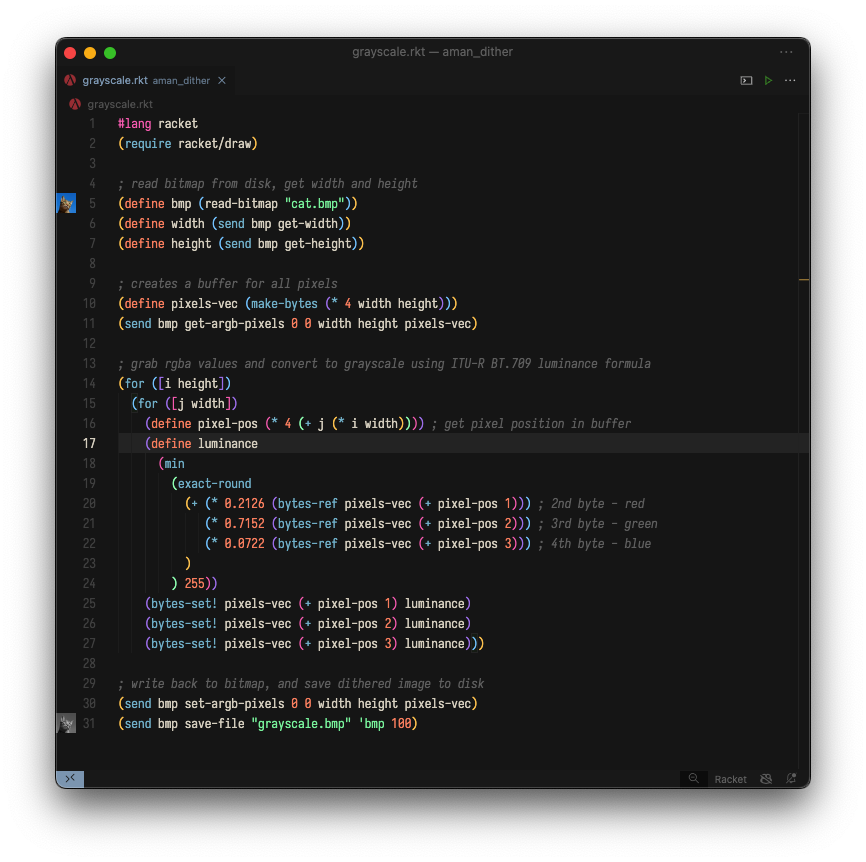
该程序使用 Racket Drawing Toolkit 从磁盘加载位图，然后创建一个缓冲区来存储位图中每个像素的信息。位图逐行遍历，从左到右，并且每个像素的 RGB 值使用转换公式转换为亮度值。然后将像素缓冲区写入新文件并保存到磁盘。
在我们的原始猫照片上运行上面的代码，我们可以得到这个：
太棒了 - 进入下一步！
阈值化
现在，我们位图中的每个像素都在灰度范围内，我们可以考虑根据像素接近哪种颜色（黑色或白色），将其向下舍入为黑色或向上舍入为白色。
这称为阈值化（或“平均抖动”）。顾名思义，我们可以选择一个任意阈值（即，一个介于 0 到 255 之间的数字），它将确定新图像中的任何给定像素变为黑色还是白色。
例如，如果我们设置阈值为 0 到 255 之间的中点，那么...
RGB(101, 101, 101) -> RGB(0, 0, 0)
因为 101 ≤ 127。
此算法的代码如下：
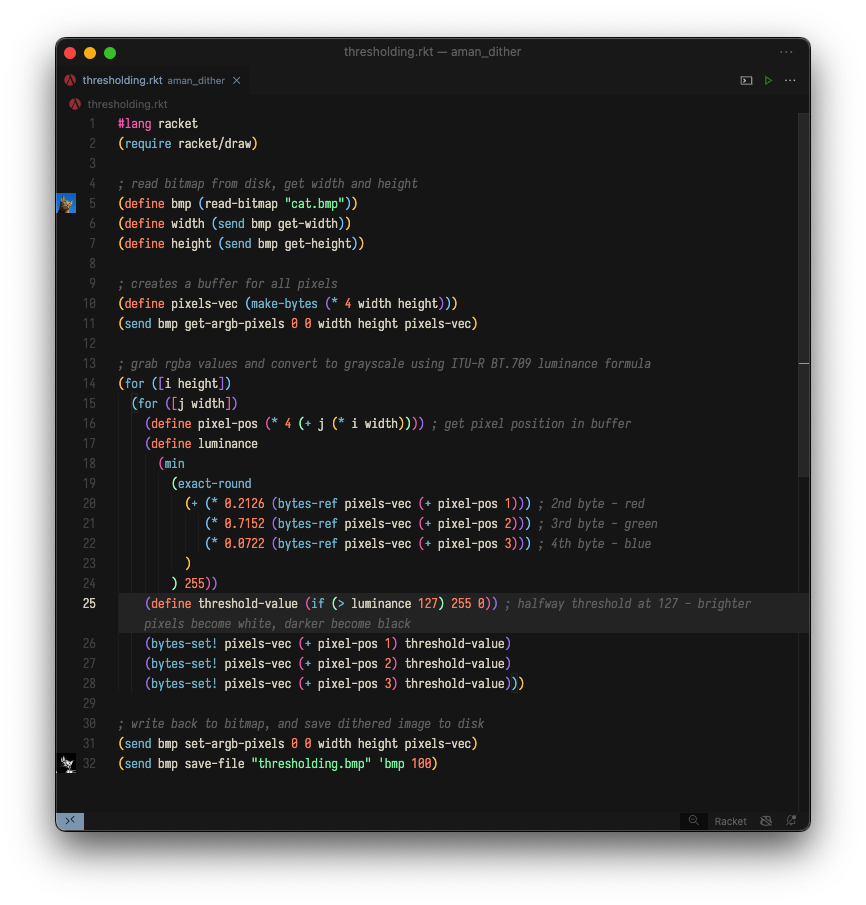
它与灰度转换的代码几乎相同，除了第 25-28 行，其中颜色值根据我们的阈值设置为黑色或白色（正好在 0 和 255 之间）。
该程序输出以下图像：
是的……阈值化不是很好。新图像中几乎整个天空现在都是黑色的，这最终与猫的一部分融为一体。
但这绝对是一个开始！阈值化终于让我们得到了一张热敏打印机可以实际打印的图像。让我们继续进行更复杂的抖动算法，希望它能给我们带来更好的结果。
误差扩散抖动
假设我们正在遍历一个灰度位图，逐行遍历，每行从左到右。对于我们处理的每个像素，我们仍然需要做出一个二元决策：选择黑色或白色作为像素的颜色。
但是，我们是否可以不对每个像素的实际亮度/灰度值进行舍弃，而是利用像素的真实亮度与我们被迫选择的二元黑色或白色值之间的差异做一些事情？
这就是误差扩散抖动的基础！与在将像素转换为黑白时单独考虑每个像素的阈值化不同，误差扩散抖动将每个像素的“量化误差”（即我们之前谈到的差异）扩散到其任何未处理的邻居。
这确保了已被向下舍入的像素的邻居更有可能被向上舍入，从而平均而言，量化误差会减少。
在上图中，我们目前正在处理以蓝色阴影显示的像素，箭头表示我们已选择将误差扩散到的所有相邻像素。
我们选择的特定邻居像素集是相当随意的，但我们在扩散模式中包含的任何邻居像素都必须是我们尚未处理的像素。在我们的示例中，这意味着我们不能将所选像素的误差扩散到标有红色 X 的两个像素。
但是，除此之外，任何一组相邻像素都可以用于抖动算法，实际上，这是不同算法之间的关键区别！
Atkinson 抖动
考虑 Atkinson dithering，这是一种由 Bill Atkinson 设计的误差扩散抖动算法，用于原始 Macintosh 计算机中。它依赖于以下扩散模式：
特定像素的量化误差的八分之一扩散到上面显示的六个相邻像素中的每一个。
这是一个使用 Atkinson 算法进行误差扩散抖动的具体示例：如果我们有一个亮度/灰度值为 178 的像素，我们将首先决定将此像素设置为白色 (255)。我们将使用这两个数字来计算此像素的误差...
178 - 255 = -77
...然后我们将此误差乘以八分之一：
-77 * (1/8) = -9.625
最后，我们将把这个误差 (-9.625) 分配/添加到图中显示的六个相邻像素中的每一个。请注意，Atkinson 抖动向外扩散任何给定像素的量化误差的四分之三：
(1/8) * 6 = (6/8) = (3/4)
看看 Racket 实现的 Atkinson 抖动的前半部分：
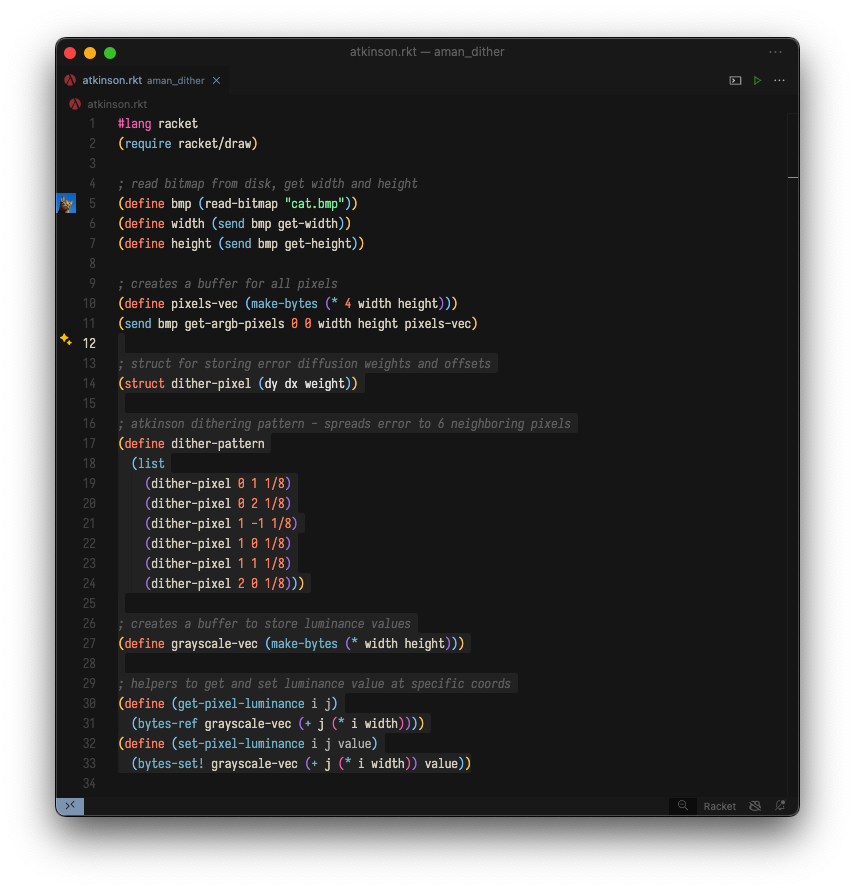
第 13-33 行是新的：我们创建一个结构体来存储误差扩散的偏移量/权重，我们创建一个这些结构体的列表来表示 Atkinson 算法中使用的误差扩散模式，并且我们创建一个新的中间缓冲区（以及一些辅助方法）来抽象出一些字节级操作。
继续到这个程序的主要部分！
这是为位图中每个像素执行误差扩散的主循环：
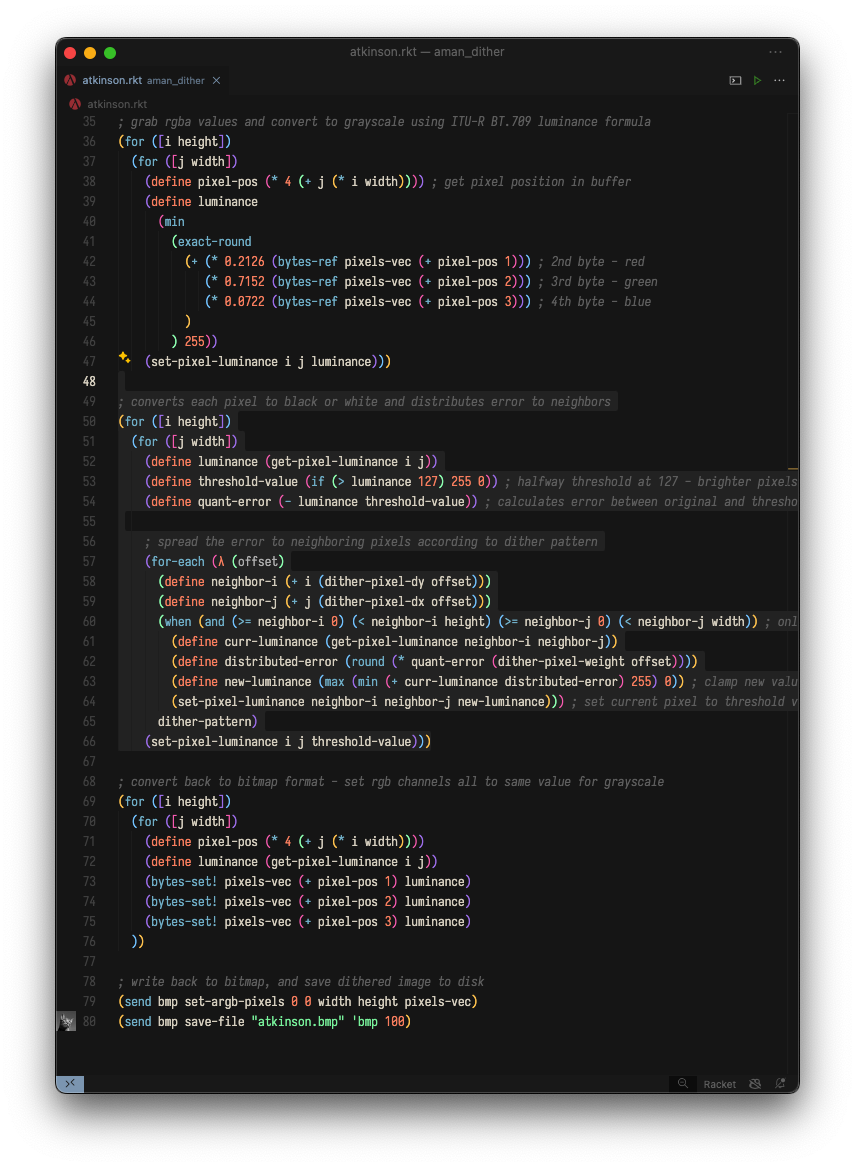
浏览这段代码，您会注意到我们正在遵循我们之前抽象讨论的相同步骤。
如果我们运行这个程序，我们成功地得到了使用 Atkinson 抖动创建的猫的单色图像：
与阈值化相比，这是一个多么大的改进！
创建新的抖动算法
Atkinson 抖动很棒，但抖动算法的优点在于没有明确的“最佳”算法！每种算法都会导致略有不同的结果。
例如，我之前提到过，Atkinson 抖动仅扩散任何给定像素的量化误差的四分之三（六个不同像素中每个像素的八分之一）。这使图像更“突出”，但也具有使图像的某些非常暗或非常亮的区域看起来“曝光过度”的不良影响。
其他误差扩散抖动算法，如 Floyd-Steinberg，往往没有这个问题，因为它们会将整个量化误差扩散到相邻像素。但是，这是以牺牲图像的对比度为代价的。
当然，什么看起来更好（以及在什么情况下）完全取决于个人喜好，但我想要创建一种 Atkinson 和 Floyd-Steinberg 之间的折中算法：一种将任何给定像素的误差的七分之八 (7/8) 精确地传播到其邻居的算法。
这是我想出的模式：
这是 Racket 代码：
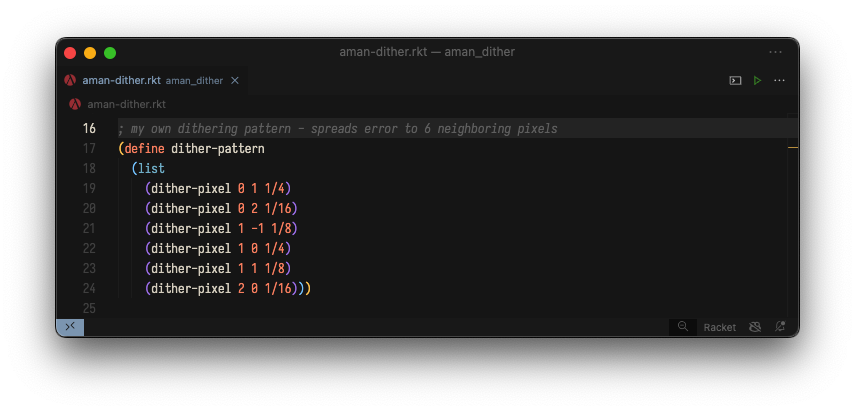
就是这样 - 这是从 Atkinson 算法的实现中所需要做的唯一更改！我自己的抖动算法诞生了。 🙃
这是应用了我的抖动算法的猫照片：
我不知道你怎么看，但我喜欢它！