ARJF Academia

Resonate

Resonate | Resonate 是一种低延迟、低内存占用和低计算成本的算法，用于评估来自音频（和其他）信号的感知相关的频谱信息。
---|---

概述

Resonate 基于一个谐振器模型，该模型使用指数加权移动平均 (Exponentially Weighted Moving Average, EWMA)（也称为信号处理中的低通滤波器）在时域中累积其谐振频率周围的信号贡献。与在线感知信号分析一致，EWMA 给予最近的输入值更高的权重，而较旧的值的贡献呈指数衰减。该模型的紧凑迭代公式可以在每个信号输入样本处计算更新，无需缓冲，并且仅涉及少量的算术运算。

每个谐振器，以其谐振频率 f=ω2π 为特征，由一个复数 R 描述，其幅度捕获输入信号分量在频率 f 附近的贡献。以下公式通过一个相位器 P 捕获 R 的递归更新，该相位器应用于每个实值输入信号 x(t)∈[−1,1] 的样本 x，该信号以采样率 sr 定期采样。 Δt=1/sr 是样本持续时间，α∈[0,1] 是一个常数参数，它决定了每个新测量对累积值的影响程度。

P←Pe−iωΔt
R←(1−α)R+αxP

这两个复数 P 和 R 捕获了谐振器的完整状态。在每个输入信号样本处更新状态只需要少量的算术运算。功率和/或幅度的计算对于更新不是必需的，并且可以仅在应用程序需要时才执行，且相对有效率。单个参数 α 可以与时间常数相关，它控制系统的动态特性。对于音频应用中感兴趣的频率范围（20-20000 Hz），函数 αf=1−e−Δtflog(1+f) 是一个合理的启发式方法。平滑状态 ˜R 通过将 EMWA 与相同的 α 应用于 R 来产生，以抑制功率和相位振荡。最后，每个谐振器的输出可以可选地通过谐振器频率的阶跃信号的总响应进行归一化（均衡）。

谐振器阵列独立地调谐到感知相关的频率尺度，实时计算输入信号的频谱内容的瞬时、感知相关的估计。这种阵列的内存和每个样本的计算复杂度都与谐振器的数量成线性关系，并且与处理的输入样本的数量或处理信号的持续时间无关。此外，由于谐振器是独立的，因此对其谐振频率或时间常数的调谐没有约束，并且所有每个样本的计算都可以跨谐振器并行化。在离线处理上下文中，给定持续时间的累积计算成本随处理的输入样本的数量线性增加。

频谱图

频谱信息作为时间的函数通常以频谱图的形式以图形方式呈现供人消费，其中水平轴代表时间，垂直轴代表频率。每个点的值代表输入信号在给定时间片中频率的功率。这些值通常通过信号的最大值进行归一化，并映射到对数颜色标度以生成如下图所示的图。一个具有适当调谐谐振器的 Resonate 振荡器阵列可以直接有效地计算任意频率尺度的频谱图，与基于 FFT 的方法相比，具有更相关的频率分辨率和更高的时间分辨率。

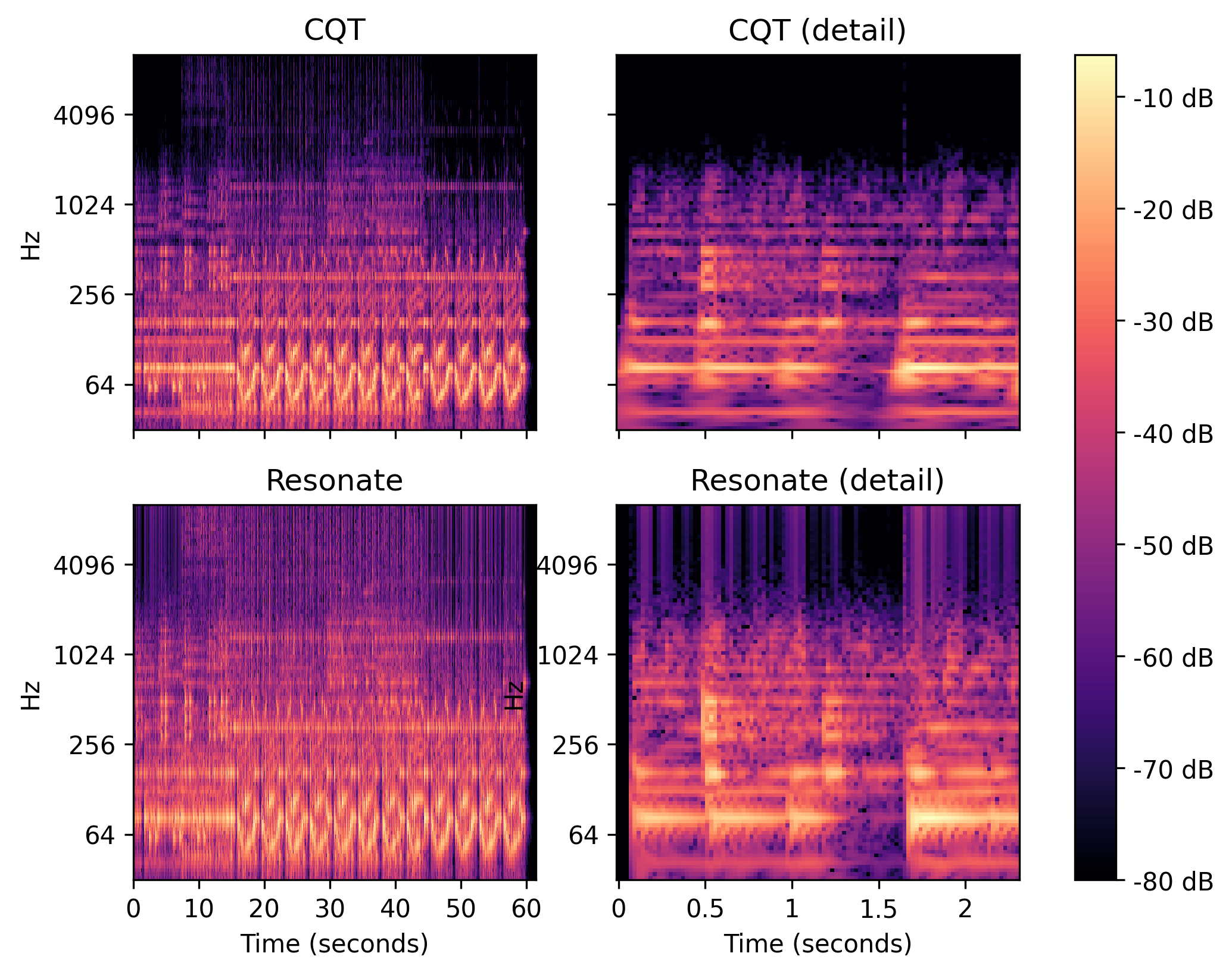对数频率刻度频谱图 从恒定 Q 变换 (CQT) 和 Resonate 实现计算的Librosa's vibeace 音乐示例的对数频率功率频谱图（频谱图显示和来自 Librosa 的 CQT，采样率：22050Hz，跳跃长度：512 个样本，从 32.7Hz 到 9955.1Hz 的 100 个频率仓，每倍频程 12 个仓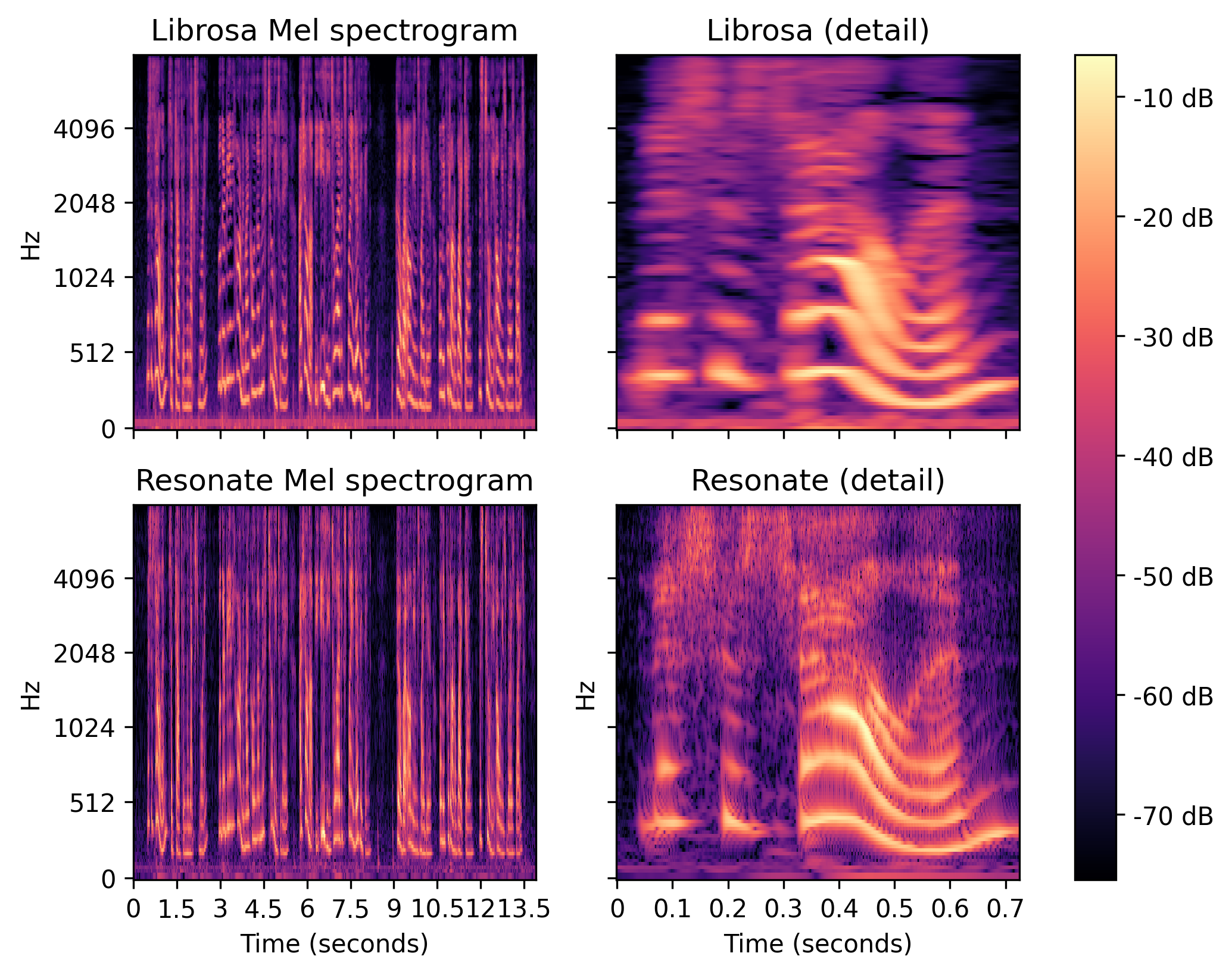）。 Mel 频率刻度频谱图 从恒定 Q 变换 (CQT) 和 Resonate 实现计算的Librosa's Libri3 语音样本的 Mel 频率功率频谱图（频谱图显示和来自 Librosa 的 CQT，采样率：22050Hz，跳跃长度：32 个样本，从 0 到 8000Hz 的 128 个频率仓）。

出版物

Alexandre R.J. François, “Resonate: Efficient Low Latency Spectral Analysis of Audio Signals,” to appear in Proceedings of the 50th Anniversary of the International Computer Music Conference 2025, Boston, MA, USA, 8-14 June 2025.

资源