没有废话的 Markov Chain Monte Carlo (2015)
没有废话的 Markov Chain Monte Carlo
#markov chain #mathematics #MCMC #monte carlo #random walk 2015-04-06
这篇文章是从我以前的 Wordpress 博客 这里 迁移过来的。如果您发现渲染或布局有任何问题,请给我发送电子邮件。
我有一个小秘密:我不喜欢统计学中的术语、符号和写作风格。我发现它不必要地复杂。这在试图阅读关于 Markov Chain Monte Carlo 方法的文章时表现得很明显。例如,以下是 Encyclopedia of Biostatistics 中 Markov Chain Monte Carlo 文章的摘要:
Markov chain Monte Carlo (MCMC) 是一种通过模拟来估计复杂模型中统计量的期望的技术。连续的随机选择形成一个 Markov 链,其平稳分布是目标分布。它对于评估复杂 Bayesian 模型中的后验分布特别有用。在 Metropolis–Hastings 算法中,项目是从任意的“提议”分布中选择的,并根据接受规则保留或不保留。Gibbs 采样器是一种特殊情况,其中提议分布是向量参数的单个分量的条件分布。考虑了各种特殊情况和应用。
我只能模糊地理解作者在这里所说的话(而且真的只是因为我事先知道 MCMC 是什么)。当然,其中提到了比我将在本文中介绍的更高级的内容。但是,似乎很难找到对 Markov Chain Monte Carlo 的解释,没有 多余的术语。这里的“废话”是作者暗示需要这些术语。也许需要它们来解释高级应用(例如尝试在 “Bayesian 网络中进行推断”),但绝对不需要它们来定义或分析基本思想。
因此,为了反驳,这是我对 Markov Chain Monte Carlo 的解释,灵感来自 John Hopcroft 和 Ravi Kannan 的处理方法。
问题是从分布中抽取样本
Markov Chain Monte Carlo 是一种解决 从复杂分布中采样 的问题的技术。让我通过以下虚构的场景来解释。假设我有一个魔盒,它可以很好地估计婴儿名字的概率。我可以给它一个像“Malcolm”这样的字符串,它会告诉我确切的概率 pMalcolm,你会为你的下一个孩子选择这个名字。因此,在所有名称上都有一个分布 D,它非常具体地反映你的偏好,并且为了论证起见,假设这个分布是固定的,你不能篡改它。
现在问题来了:我想 有效地从 这个分布 D 中抽取一个名字。这就是 Markov Chain Monte Carlo 旨在解决的问题。为什么这是一个问题?因为我不知道你用什么过程来选择名字,所以我无法自己模拟这个过程。这是你可以尝试的另一种方法:均匀随机地生成一个名字 x,询问机器 px,然后抛一枚概率为 px 的有偏差的硬币,如果硬币正面朝上则使用 x。问题在于,名字的数量呈指数增长!这里的变量是写下一个名字所需的位数 n=|x|。因此,要么概率 px 将呈指数级的小,并且我将抛掷很长时间才能获得一个名字,要么只有少数几个具有非零概率的名字,并且我将需要呈指数级的抽取次数才能找到它们。效率低下是我的死穴。
所以这是一个严重的问题!让我们正式地重申它,以明确说明。
定义(抽样问题): 设 D 是有限集合 X 上的分布。你可以通过黑盒访问概率分布函数 p(x),该函数输出根据 D 绘制 x∈X 的概率。设计一种高效的随机算法 A,该算法输出 X 的一个元素,以便输出 x 的概率近似等于 p(x)。更一般地,输出从 X 中根据 p(x) 抽取的元素样本。
假设 A 只能访问公平的随机硬币,尽管这允许人们有效地模拟抛掷 任何所需概率的有偏差的硬币。
请注意,使用这样的算法,我们将能够做一些事情,例如估计某个随机变量 f:X→R 的期望值。我们可以通过抽样问题的解决方案获取一个大的样本 S⊂X,然后计算 f 在该样本上的平均值。这就是 Monte Carlo 方法在抽样很容易时所做的事情。事实上,抽样问题的 Markov Chain 解决方案将允许我们一次性完成抽样 和 E(f) 的估计(如果你愿意)。
但核心问题确实是一个抽样问题,“Markov Chain Monte Carlo” 更准确地称为“Markov Chain 抽样方法”。因此,让我们看看 Markov Chain 如何可能帮助我们。
随机游走,MCMC 的“Markov Chain”部分
Markov Chain 本质上是一个图上的随机游走的炫酷术语。
你给我一个有向图 G=(V,E),对于每条边 e=(u,v)∈E,你给我一个数字 pu,v∈[0,1]。为了使随机游走有意义,pu,v 需要满足以下约束:
对于任何顶点 x∈V,所有出边 (x,y) 上的所有值 px,y 的总和必须为 1,即形成一个概率分布。
如果满足此条件,那么我们可以根据概率在 G 上进行随机游走,如下所示:从某个顶点 x0 开始。然后根据出边上的概率随机选择一个出边,并沿着它到达 x1。如果可能,则重复。
我说“如果可能”是因为任意图不一定具有从给定顶点发出的任何出边。我们需要对图施加一些额外的条件,以便将随机游走应用于 Markov Chain Monte Carlo,但在任何情况下,随机游走的思想都是明确定义的,我们将整个对象 (V,E,{pe}e∈E) 称为 Markov 链。
这是一个示例,其中图中的顶点对应于情绪状态。
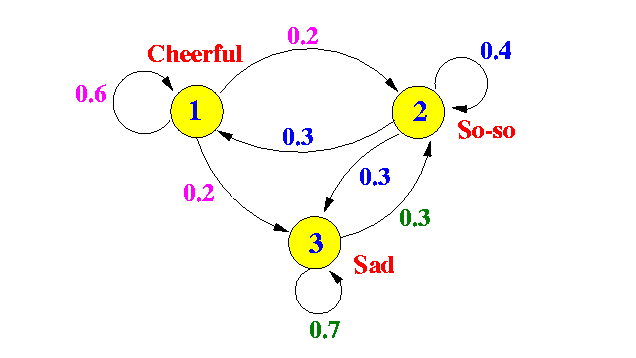
一个示例 Markov 链
在统计领域,他们非常重视随机游走的“状态”解释。他们称边概率为“状态到状态的转换”。我们需要使用 Markov 链来做任何有用的事情的主要定理是平稳分布定理(有时称为 “Markov 链基本定理”,这是有充分理由的)。它直观地表示,对于非常长的随机游走,你最终停留在某个顶点 v 的概率与你从哪里开始无关!所有这些概率放在一起被称为随机游走的 平稳分布,它由 Markov 链唯一确定。
然而,由于我们上面陈述的原因(“如果可能”),平稳分布定理并非对每个 Markov 链都成立。我们需要的主要属性是图 G 是 强连通的。回想一下,如果忽略方向,从每个顶点到每个其他顶点都有一条路径,则称有向图是连通的。如果考虑方向时仍然可以在任何地方获得路径,则称其为 强连通的。如果我们另外要求没有边可以具有零概率的愚蠢的边界情况捕获器,那么强连通性(图的一个分量)等效于以下属性:
对于每个顶点 v∈V(G),从 v 开始的无限随机游走将以概率 1 返回到 v。
事实上,它会无限次返回。统计学家称此属性为状态 v 的 持久性。我不喜欢这个术语,因为它似乎描述了顶点的属性,而对我来说,它描述了包含该顶点的连通分量的属性。在任何情况下,由于在 Markov Chain Monte Carlo 中,我们将选择要行走的图(剧透!),我们将通过设计来确保该图是强连通的。
最后,为了以更熟悉的方式(使用线性代数)描述平稳分布,我们将转换概率写成矩阵 A,其中条目 aj,i=p(i,j),如果存在边 (i,j)∈E,否则为零。这里行和列对应于 G 的顶点,每个 列 i 形成从状态 i 到随机游走中的某个其他状态的概率分布。请注意,A 是有向加权图 G 的加权邻接矩阵的转置,其中权重是转换概率(我这样做是因为矩阵向量乘法将矩阵放在左边而不是右边;参见下文)。
这个矩阵允许我使用线性代数的语言来很好地描述事物。特别是,如果你给我一个基向量 ei,解释为“随机游走当前在顶点 i”,那么 Aei 给出一个向量,其第 j 个坐标是在随机游走中再走一步后,随机游走将位于顶点 j 的概率。同样,如果你给我一个顶点上的概率分布 q,那么 Aq 给出一个概率向量,解释如下:
如果随机游走以概率 qi 处于状态 i,那么 Aq 的第 j 个条目是在随机游走中再走一步后到达顶点 j 的概率。
以这种方式解释,平稳分布是一个概率分布 π 使得 Aπ=π,换句话说,π 是 A 的特征值为 1 的特征向量。
对于这个博客的忠实读者来说,一个简短的旁注是:这种对随机游走的分析与我们在本博客早期研究用于对网页进行排名的 PageRank 算法 时所做的完全相同。在那里,我们将矩阵 A 称为 “web 矩阵”,对其进行随机游走,并找到一个特殊的特征值,其特征向量是一个“平稳分布”,我们用它来对网页进行排名(这使用了称为 Perron-Frobenius 定理 的东西,该定理说随机游走矩阵具有该特殊的特征向量)。在那里,我们描述了一种通过迭代相乘 A 来实际找到该特征向量的算法。以下定理本质上是该算法的一种变体,但在较弱的条件下有效;对于 web 矩阵,我们添加了额外的“伪造”边,这些边提供了所需的更强的条件。
定理: 设 G 是一个强连通图,其相关的边概率 {pe}e∈E 形成一个 Markov 链。对于概率向量 x0,定义 xt+1=Axt 对于所有 t≥1,并让 vt 为长期平均值 vt=1t∑s=1txs。然后:
- 存在一个唯一的概率向量 π 使得 Aπ=π。
- 对于所有 x0,极限 limt→∞vt=π。
证明。 由于 vt 是一个概率向量,我们只想证明当 t→∞ 时,|Avt–vt|→0。实际上,我们可以将此数量展开为 Avt–vt=1t(Ax0+Ax1+⋯+Axt−1)–1t(x0+⋯+xt−1)=1t(xt–x0) 但是 xt,x0 是单位向量,所以它们的差最多为 2,这意味着 |Avt–vt|≤2t→0。现在很明显,这不依赖于 v0。为了唯一性,我们将放弃并诉诸 Perron-Frobenius 定理,该定理表明这种形式的任何矩阵都具有唯一的此类(归一化)特征向量。 ◻
一个额外的说明是,除了通过实际计算该平均值或使用特征求解器来计算平稳分布之外,还可以通过分析方式将其求解为特定矩阵的逆矩阵。定义 B=A−In,其中 In 是 n×n 单位矩阵。设 C 为 B,并在底部附加一行 1,并删除最顶行。然后可以(非常不透明地)证明 C−1 的最后一列是 π。我们将此留给读者作为练习,因为我很确定在实践中没有人使用此方法。
最后一个说明是关于为什么我们需要对上述定理中的所有 xt 取平均值。可以添加到强连通性的一个额外的技术条件,称为 非周期性,它允许人们加强该定理,以便 xt 本身收敛于平稳分布。严格地说,非周期性是指,无论你从哪里开始随机游走,经过足够大的步数 n 之后,随机游走在随后的每个步骤中都有正概率位于每个顶点。作为一个非周期性失败的图的示例:偶数个顶点的无向循环。在这种情况下,只有在_每隔一步_ 的某些顶点上存在正概率,并且对这两个长期序列求平均值会给出实际的平稳分布。
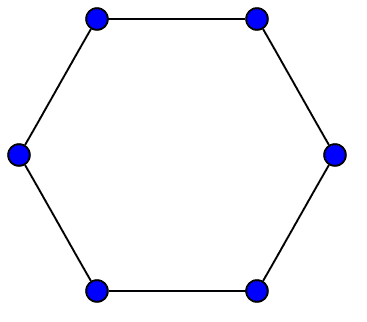
图片来源:Wikipedia
保证您的 Markov 链是非周期性的一种方法是确保在任何顶点都有正概率停留。也就是说,您的图有一个自循环。这就是我们将在下一节中要做的事情。
构建一个可以行走的图
回想一下,我们试图解决的问题是从具有概率函数 p(x) 的有限集合 X 上的分布中抽取样本。MCMC 方法是构建一个 Markov 链,其平稳分布正是 p,即使您只有对评估 p 的黑盒访问权限。也就是说,你(隐式地)选择一个图 G 并(隐式地)选择边的转换概率以使平稳分布为 p。然后,您在 G 上进行足够长的随机游走,并输出与您最终停留在的任何状态相对应的 x。
简单部分是想出一个具有正确平稳分布的图(事实上,“大多数”图都可以工作)。困难的部分是想出一个图,你可以证明随机游走到平稳分布的收敛速度与 X 的大小相比是很快的。这样的证明超出了本文的范围,但对图的 “正确” 选择并不难理解。
我们将在本文中选择的图称为 Metropolis-Hastings 算法。输入是你对 p(x) 的黑盒访问权限,输出是一组规则,这些规则隐式地定义了在顶点集合为 X 的图上的随机游走。
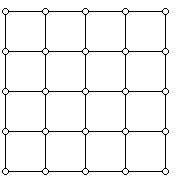
它的工作方式如下:你选择某种方式将 X 放在一个格子上,以便每个状态对应于 {0,1,…,n}d 中的某个向量。然后,您向所有相邻的格点添加(双向有向)边。对于 n=5,d=2,它看起来像这样:
图片来源 http://www.ams.org/samplings/feature-column/fcarc-taxi
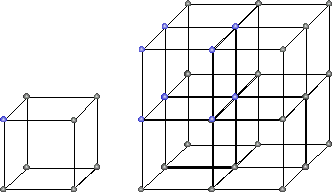
对于 d=3,n∈{2,3},它看起来像这样:
lattice
你必须小心,以确保你为 X 选择的顶点不是断开连接的,但在许多应用中,X 自然已经是一个格子。
现在我们必须描述转换概率。令 r 为该格子中顶点的最大度数 (r=2d)。假设我们位于顶点 i 并且我们想知道下一步要去哪里。我们这样做:
- 以概率 1/r 选择邻居 j(有一些机会留在 i)。
- 如果你选择了邻居 j 并且 p(j)≥p(i),那么确定性地去 j。
- 否则,p(j)<p(i),并且你以概率 p(j)/p(i) 去 j。
我们可以将边 (i,j) 上的概率权重 pi,j 更紧凑地表示为 pi,j=1rmin(1,p(j)/p(i))pi,i=1–∑(i,j)∈E(G);j≠ipi,j 很容易检查出对于每个顶点 i,这确实是一个概率分布。因此,我们只需要证明 p(x) 是此随机游走的平稳分布。
这是一个事实:如果一个概率分布 v,其中每个 x∈X 的条目为 v(x),具有属性 v(x)px,y=v(y)py,x 对于所有 x,y∈X,则 v 是平稳分布。为了证明它,固定 x 并对该方程的两边求和所有 y。结果正是方程 v(x)=∑yv(y)py,x,这与 v=Av 相同。由于平稳分布是唯一满足该方程的向量,因此 v 必须是它。
使用我们选择的 p(i) 很容易做到这一点,因为通过对定义应用一点代数,p(i)pi,j 和 p(i)pj,i 都等于 1rmin(p(i),p(j))。所以我们完成了!人们可以根据这些概率随机行走并获得样本。
最后的话
我想说的关于 MCMC 的最后一件事是,你可以同时估计函数 E(f) 的期望值,同时在你的 Metropolis-Hastings 图(或任何平稳分布为 p(x) 的图)中随机行走。根据定义,f 的期望值为 ∑xf(x)p(x)。
现在我们可以做的是仅在我们随机游走期间访问过的状态中计算 f(x) 的平均值。通过一些额外的工作,你可以证明此数量将在随机游走收敛到平稳分布的同时,收敛到 f 的真实期望值。(这里的“大约”意味着我们与一个取决于 f 的常数因子相差甚远)。为了证明这一点,你需要一些额外的工具,我太懒了,无法在本文中进行介绍,但重点是它可以工作。
我没有首先从估计函数的期望值方面描述 MCMC 的原因是,核心问题是一个抽样问题。此外,MCMC 的许多应用只需要一个样本。例如,MCMC 可用于估计任意(可能高维)凸集的体积。请参阅 Alistair Sinclair 的 这些讲义 了解更多信息。
如果需求足够大,我可以用代码实现 Metropolis-Hastings 算法(它不会达到行业强度,但也许会启发人?我不确定……)。
下次再见!
想要回复?给我发送电子邮件,发布 webmention,或在 互联网上的其他地方 找到我。