前进的事件：iCalendar 与光线步进有何关联？（Marching Events: What does iCalendar have to do with ray marching?）

Marching Events: What does iCalendar have to do with ray marching?

Source | HN Comments

文章探讨了如何使用 iCalendar 的重复事件规则，并将其与光线步进技术联系起来。作者将 iCalendar 的重复规则转化为类似 SQL 的查询，并借鉴光线步进中的有符号距离函数（SDF）概念，构建了用于计算重复事件发生时间的距离函数。通过组合这些距离函数，可以高效地确定事件的下一次发生时间，从而避免了传统方法中复杂的逻辑判断，并简化了代码实现。文章还讨论了如何通过“或”和“与”操作符组合规则，以及优化算法的思路。

Marching Events: iCalendar 与光线步进有何关联？

2025-04-16 #ical #rust 最近，我有幸（也可能是不幸）实现了一个用于操作 iCalendar 文件的库。如果你没听说过它，但你可能已经用过它 - 它是用于传输电子邮件 RSVP 的格式，例如：

尽管 iCal 已经有些年头了——RFC 2245 的日期是 1998 年，与克林顿-莱温斯基丑闻同年——但我认为它是一种非常好的格式™。它相当容易打印和解析：

BEGIN:VEVENT
UID:1234-1234-1234-1234
DTSTAMP:20250608T160000Z
DTSTART:20250628T160000Z
DTEND:20250628T190000Z
SUMMARY:在邻居的垃圾中发现了一些好蜡烛，准备吸食。
CATEGORIES:BUSINESS
END:VEVENT

...并且支持很多东西——今天，我们要重点关注重复事件。

这是一个约会！

我是一个简单的人——对我来说，重复意味着像“每天”或“每周”这样简单的事情；但世界并非如此简单。

每天每小时每周每个月第二个星期一从 2018-02-29 开始的每年每三年最后一个星期三每隔一月的每个第四个星期日，时间为 12:34:56 每个月最后一个星期二，从 2018-03 开始的每个第五个月的中午从 2018-04 开始的每个月最后一个工作日，除非是 2018-01-01

我们如何驯服它？ iCalendar 建议我们定义：

FREQ，说明事件重复的频率（每小时、每天、每周……），
DTSTART，说明事件从何时开始重复，

...这基本上就是全部了，至少就必需属性而言：

FREQ=HOURLY;DTSTART=20180101T120000

-> 2018-01-01 12:00:00
-> 2018-01-01 13:00:00
-> 2018-01-01 14:00:00
-> [...]

我们还可以指定 INTERVAL，它产生频率的倍数：

FREQ=DAILY;INTERVAL=3;DTSTART=20180101T120000

-> 2018-01-01 12:00:00
-> 2018-01-04 12:00:00
-> 2018-01-07 12:00:00
-> [...]

但这很无聊，这是你自己也能想到的——这里有一些有趣的东西：

FREQ=MONTHLY;INTERVAL=2;BYMONTHDAY=1,-1;BYDAY=MO;DTSTART=20180101

从 2018-01 开始，每隔一个月重复一次，在每个月的第一个和最后一个日期，但
仅当该天是星期一时：
-> 2018-01-01
-> 2019-07-01
-> 2019-09-30
-> 2020-11-30

...这里有一些实用的东西：

FREQ=MONTHLY;BYDAY=MO,TU,WE,TH,FR;BYSETPOS=-1;DTSTART=20180131

从 2018-01 开始，在每个月的最后一个工作日重复：
-> 2018-01-31 (星期三)
-> 2018-02-28 (星期三)
-> 2018-03-30 (星期五)
-> [...]

你可能会看到它的走向：给定一个 iCal 公式，我们如何找出它何时重复？

计算机之爱

听起来容易，对吧？或者可能不是非常容易，但——就像——可行的。即使你意识到潜在的障碍（重复如何在时区转换中定义？），你可能也会想到，从_直觉上_来说，实现这件事不应该非常困难。

而且你在某种程度上是对的。大多数实现都倾向于具有某种手动展开的、特定于频率的逻辑：

fniter(recur:&Recur)->implIterator<Item=DateTime>{
matchrecur.freq{
"yearly"=>iter_yearly(recur),
"monthly"=>iter_monthly(recur),
"daily"=>iter_daily(recur),
/* ... */
}
}
/* ... */
fniter_monthly(recur:&Recur)->implIterator<Item=DateTime>{
letmutcurr=recur.dtstart;
loop{
ifrecur.by_month_day.is_empty(){
// FREQ=MONTHLY;INTERVAL=3 只是简单地使用
// 连续的、基于频率的增量来重复 DTSTART
yieldcurr;
}else{
// FREQ=MONTHLY;BYMONTHDAY=10,20,30 创建*新的*日期，这些日期是
// 基于当前迭代的日期
fordayinrecur.by_month_day{
yieldcurr.with_day(day);
}
}
curr+=Span::Year*recur.interval;
}
}
/* ... */

这是因为根据上下文，参数可以用作过滤器：

FREQ=DAILY;BYDAY=MO

fordayindays_since(dtstart){
ifday.is(Monday){
yieldday;
}
}

...或者作为生成器：

FREQ=MONTHLY;BYDAY=MO

formonthinmonths_since(dtstart){
fordayinmonth.every(Monday){
yieldday;
}
}

RFC 将所有这些情况收集到一个相当可怕的表格中：

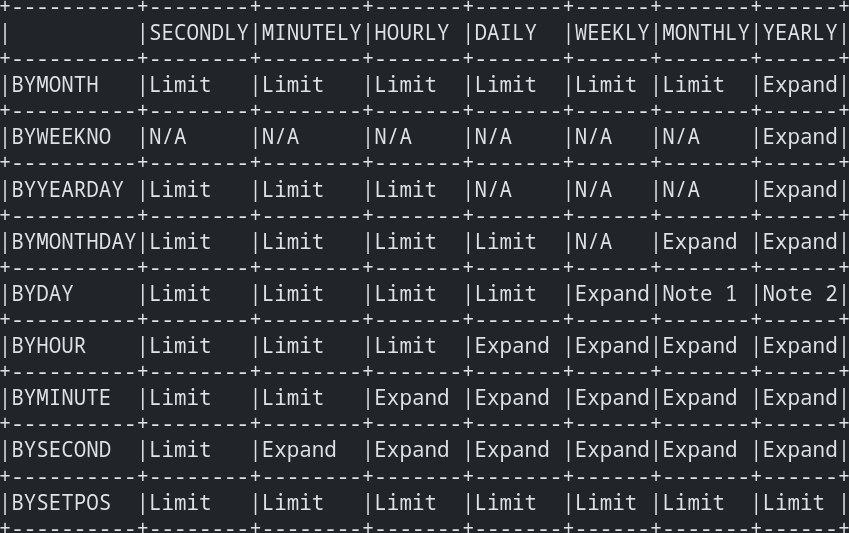
...其明显的复杂性导致库仅部分实现 iCal 功能，例如 libical 和 BYSETPOS 规则——因为它必须为它出现的每个上下文提供，所以自然只为常见的用例实现。 (不是对 libical 的吹毛求疵，这只是一个我意识到的例子。) 这也是我开始实现的方式，但有些东西让我感觉不对劲——我感觉必须有一种更好的方法来处理它。我开始将那些重复规则想象成 SQL 查询：

FREQ=DAILY;BYDAY=MO;DTSTART=20180101

selectday
fromdates-- 所有可能日期的无限表
whereday_of_week(day)='Monday'
andday>='2018-01-01'

FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10;DTSTART=20180101

selectday
fromdates
whereday_of_week(day)='Monday'orday_of_week(day)='Tuesday'
andday_of_month(day)=10
andday>='2018-01-01'

...然后我意识到，在这个框架下，FREQ 规则消失了——FREQ=DAILY;BYDAY=MO、FREQ=WEEKLY;BYDAY=MO 和 FREQ=MONTHLY;BYDAY=MO 都对应于相同的查询，即使在一种情况下 BYDAY 用作过滤器，而在其他情况下它是一个生成器：

FREQ=DAILY/WEEKLY/MONTHLY;BYDAY=MO;DTSTART=20180101

selectday
fromdates
whereday_of_week(day)='Monday'
andday>='2018-01-01'

有了这个，我开始思考如何实现这个查询——天真地，我们可以简单地遍历所有可能的日期，并检查是否所有条件都匹配（模 >= '2018-01-01' 部分，因为这个假设的 dates 表是无限的）。但也许有更好的方法？然后我意识到我可以从渲染社区 ~~偷~~ 借用一些东西。

爱的三角形的数学

三角形是那些尖尖的、性感的家伙：

...它们的生活目的是说明 ~~Pytagorean~~ ~~Pythagoran~~ ~~Pytagoream~~ 毕达哥拉斯定理——它们也倾向于用于对计算机图形学中的东西进行建模，以及诸如此类的东西：

https://commons.wikimedia.org/wiki/File:CG_WIKI.jpg

三角形很酷，因为 GPU 每秒可以绘制数百万个三角形，但渲染中的简单性是有代价的。某些操作——比如找出两个形状的差异：

...当在三角形（又名多边形）上操作时，会相当麻烦。思考形状的另一种方式是通过分析的方式来描述它们，最流行的方法（需要引用）是通过有符号距离函数。有符号距离函数接受一个点，并返回从该点到最近表面的距离。你可能认为实现它听起来很困难，但实际上非常简单——例如，半径=1 的球体（中心位于 xyz=(0,0,0)）的 SDF 只是：

structVec3{
x:f32,
y:f32,
z:f32,
}
fnsphere(point:Vec3)->f32{
// 计算从原点 (0,0,0) 到给定点的距离
letdist_to_origin=(
point.x*point.x
+point.y*point.y
+point.z*point.z
).sqrt();
dist_to_origin-1.0
}

...因为：

sphere(vec3(2.0,2.0,2.0))=~2.46
// ^ 我们距离最近的球体 2.46 个单位
sphere(vec3(0.57,0.57,0.57))=~0.0
// ^ 我们正好*在*球体上 (0.57 = 1/sqrt(3))
sphere(vec3(0.0,0.0,0.0))=-1.0
// ^ 我们在球体表面过去了 -1.0 个单位（我们在形状内部）

值得注意的是，当给定点直接位于函数表示的表面上时，SDF 返回零——因此，如果我们想渲染这个表面，我们将使用一个相机：

...和一个视口（我们要在其上投影图像的画布）：

...然后对于这个视口的每个像素，我们将从相机发射一条光线，穿过视口，向外射向世界：

...我们将缓慢地沿着每条光线前进，寻找 SDF 返回零的位置，表明特定的光线已到达表面：

fnrender_image(
sdf:fn(Vec3)->f32,
camera:Camera,
)->Image{
letmutimage=Image::new(width,height);
forxin0..width{
foryin0..height{
letmutcurr=camera.origin;
letdir=camera.ray((x,y));
for_iterin0..128{
ifsdf(curr)==0.0{
// 耶，到达表面了！
image.set_color(x,y,Color::Green);
break;
}
// 不，还没 - 向前走一小步！
curr+=0.01*dir;
}
}
}
image
}

然而，以恒定的步长前进效率很低——它没有很好地利用 SDF，因为它将其视为一个二元函数（0 => yay，!= 0 => nay），而实际上 SDF 告诉我们更多。

我们可以使用从 SDF 返回的值作为指导，告诉我们应该走多长的步长，而不是采取恒定长度的步长——这被称为 球体追踪：

for_iterin0..128{
letstep=sdf(point);
ifstep==0.0{
image.set_color(x,y,Color::White);
break;
}
curr+=step*dir;
}

你可能会想：

但是因为该函数告诉我们最近的表面在哪里，我们不能简单地调用一次该函数，在 O(1) 中完成吗？为什么要循环？？

不幸的是，我们必须多次调用 SDF，因为此函数仅告诉我们到最近表面的距离，而不是到与我们行进方向一致的最近表面的距离：

因此，具体的属性是，当我们在表面时，SDF 返回零，否则它返回到最近表面的距离，或者最多是对该距离的低估。

前进的事件

酷，但这与重复事件有什么关系？

我找到了一种通过距离函数描述事件发生的方式。这意味着，我们可以简单地将几个距离函数组合在一起，而不是为频率和参数的所有组合实现逻辑——正如之前那个可怕的表格所暗示的那样。

我们最终得到的是 7 + 9，而不是 7（频率）* 9（BY* 参数）个代码路径。

与 SDF 类似，我们正在寻找的是一个接受日期、返回一个跨度（+1 小时、+2 天等）的函数，并满足以下属性：

如果 date 是事件的发生，则此函数返回零，
否则，此函数返回一个正跨度，该跨度指向下一次事件发生，或者对它的低估。

将这些作为唯一的要求意味着我们在实现方面有很多回旋余地——事实上，想出一个基本的距离函数只需几行代码：

typeDistFn=Box<dynFn(Date)->Span>;
fncompile_recur(recur:&Recur)->DistFn{
Box::new(move|curr:Date|->Span{
// 检查 `curr` 是否匹配任何 `BYDAY` 规则
// (如果 `by_day` 为空，则计算结果为 `true`)
letmatches_by_day=recur.by_day.iter().any(|wd|{
curr.weekday()==wd
});
// 检查 `curr` 是否匹配任何 `BYMONTHDAY` 规则
// (当 `by_month_day` 为空时，则计算结果为 `true`)
letmatches_by_month_day=recur.by_month_day.iter().any(|md|{
curr.month_day()==md
});
/* ... */
letmatches_all=
matches_by_day
&&matches_by_month_day
&&/* ... */;
ifmatches_all{
// 如果所有规则都满足，太棒了！——返回零，因为
// 这个日期一定是底层事件的发生。
Span::zero()
}else{
// 如果任何规则都不匹配，则猜测下一次
// 发生的时间。 我们可以低估，但不能高估，所以让我们取一秒钟的
// epsilon - 不会出错的！
//
// (这是因为重复规则不支持毫秒 - 一个
// 秒是最低单位。)
Span::seconds(1)
}
})
}

现在我们有了这个神奇的东西，我们能用它做什么？我们前进！

fniter(
dist:DistFn,
dtstart:Date,
)->implIterator<Item=Date>{
// 从事件重复的第一个日期开始
letmutcurr=dtstart;
loop{
// 调用距离函数并记下步长
letstep=dist(curr);
// 如果步长为零，则表示 `curr` 是 `event` 的重复 -
// 在这种情况下，我们可以简单地将其返回给调用者。
//
// 相反，非零步长告诉我们如何更接近
// 下一次发生； 不一定直接在它那里，只是更接近。
ifstep.is_zero(){
yieldcurr;
// 与光线步进相比，我们在这里感兴趣的不是
// 第一次发生，而是*所有*的发生 - 因此在达到
// `dist` 的根之后，让我们添加一个任意小的跨度，以使
// 在下一次迭代中再次滚动。
//
// 如果没有这个，下一次迭代将再次返回 `curr`，
// 永远，因为 `step` 为零。
curr+=Span::seconds(1);
}else{
curr+=step;
}
}
}

嘿，这很愚蠢，你只是在迭代所有可能的日期

你是对的！到目前为止，我们得到的本质上是：

fniter(
recur:&Recur,
dtstart:Date,
)->implIterator<Item=Date>{
letmutcurr=dtstart;
loop{
ifrecur.matches(curr){
yieldcandidate;
}
curr+=Span::seconds(1);
}
}

...这_是_愚蠢的——例如，给定：

FREQ=DAILY;BYSECOND=0,10,20;DTSTART=20180101T120000

...该算法将执行：

curr = 2018-01-01 12:00:00
iteration 1:
  # 12:00:00 匹配 BYSECOND=0,10,20
  yield curr
  curr += 1 second
iteration 2:
  # 12:00:01 不匹配 BYSECOND=0,10,20
  curr += 1 second
iteration 3:
  # 12:00:02 不匹配 BYSECOND=0,10,20
  curr += 1 second
iteration 4:
  # 12:00:03 不匹配 BYSECOND=0,10,20
  curr += 1 second
/* ... */
iteration 11:
  # 12:00:10 匹配 BYSECOND=0,10,20
  yield curr
  curr += 1 second

...这需要大量的迭代，我同意——但重要的是结果是正确的。

它是低效的，是的——但是正确的。这意味着我们的方法是合理的，我们只需要找到一种方法使其更有效、更实用；我们需要对其进行优化。当然，我们还必须实现更多的规则，例如，很方便的是，我们跳过了 FREQ 规则应该如何工作，但不用担心——我们会到达那里。

原子

让我们忽略时间片刻。没有时间。零。空。幸福。还记得 Jeff 曾经对你说过刻薄的话吗？不，你不记得，因为没有时间。

嗯，无论如何。让我们关注日期，例如 2018-01-01——假设我们有以下规则：

FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10;DTSTART=20180101

...这对应于这个伪 SQL：

selectday
fromdates
whereday_of_week(day)='Monday'orday_of_week(day)='Tuesday'
andday_of_month(day)=10
andday>='2018-01-01'

我们如何从这里走向一个好的距离函数？逐步地。让我们先处理 day_of_week。

忽略它出现的上下文，我们_希望_理想的 day-of-week 距离函数如何工作？我们可以提出几个例子：

(day-of-week Monday 2018-01-01) = 0
// 2018-01-01 是星期一
(day-of-week Tuesday 2018-01-01) = +1d
// 2018-01-01 距离星期二有一天
(day-of-week Friday 2018-01-01) = +5d
// 2018-01-01 距离星期五有五天

由于我们不关心时光倒流，我们也可以这样说：

(day-of-week Monday 2018-01-02) = +6d
// 从技术上讲，2018-01-02 距离最近的星期一 (2018-01-01) 有 -1d，
// 但由于我们希望返回的跨度是正数，让我们选择下一个
// 星期一 (2018-01-08)，它距离 2018-01-02 有 +6d

请注意，时光倒流可能是一个有用的属性。如果我们的函数是一个_有符号_距离函数，我们可以实现一个在两个方向上都有效的迭代器，也就是说，我们可以同时拥有 find_next_occurrence() 和 find_prev_occurrence()。但由于通常是人们想要找到的下一次事件发生，我们将只关注它们。

现在我们有几个例子了，是时候提出一个实现了——我们将使用 Jiff 作为我们算法的基础，因为我已经有机会使用它并且它非常令人愉快。在我们进入代码之前，我们将简化一件事——我们将继续使用 fn(Date) -> Date 而不是处理 fn(Date) -> Span，其中 span.is_zero() 条件编码为函数返回与输入日期相同的日期：

(day-of-week Monday 2018-01-01) = 2018-01-01
(day-of-week Tuesday 2018-01-01) = 2018-01-02
(day-of-week Friday 2018-01-01) = 2018-01-05

这并没有真正改变任何东西，我们只是让我们的生活更轻松，因为实际上处理日期往往比处理跨度更容易。废话不多说：

usejiff::Span;
usejiff::civil::{Date,Weekday};
enumRule{
DayOfWeek(Weekday),
}
implRule{
fnnext(&self,curr:Date)->Date{
matchself{
Rule::DayOfWeek(wd)=>{
curr+Span::new().days(curr.weekday().until(*wd))
}
}
}
}

这并不难，对吧？我们可以确认它是否按预期工作：

在 playground 中打开

#[cfg(test)]
modtests{
usesuper::*;
#[track_caller]
fndate(s:&str)->Date{
s.parse().unwrap()
}
#[test]
fnday_of_week(){
assert_eq!(
date("2018-01-01"),
Rule::DayOfWeek(Weekday::Monday)
.next(date("2018-01-01"))
);
assert_eq!(
date("2018-01-02"),
Rule::DayOfWeek(Weekday::Tuesday)
.next(date("2018-01-01"))
);
assert_eq!(
date("2018-01-05"),
Rule::DayOfWeek(Weekday::Friday)
.next(date("2018-01-01"))
);
assert_eq!(
date("2018-01-08"),
Rule::DayOfWeek(Weekday::Monday)
.next(date("2018-01-02"))
);
}
}

好的，所以距离函数似乎并不像它们看起来那么可怕！或者至少这个不是，但我可以告诉你它们中的大多数都同样直观。

继续讨论 day-of-month——和以前一样，首先让我们想象一下我们希望它的行为方式：

(day-of-month 14 2018-01-14) = 2018-01-14
// 2018-01-14 已经是当月的第 14 天
(day-of-month 16 2018-01-14) = 2018-01-16
// 2018-01-16 是从 2018-01-14 开始的最近的当月第 16 天 (+2d)
(day-of-month 12 2018-01-14) = 2018-02-14
// 2018-01-12 是从 2018-01-14 开始的最近的当月第 12 天 (-2d)，
// 但这对应于一个负跨度，所以我们跳到下个月

实现这个有点棘手，但没有危险——有三个边缘情况：

/* ... */
usestd::cmp::Ordering;
enumRule{
/* ... */
DayOfMonth(i8),
}
implRule{
fnnext(&self,curr:Date)->Date{
matchself{
/* ... */
Rule::DayOfMonth(day)=>{
matchcurr.day().cmp(day){
// E.g. curr=2018-01-14 and day=16
Ordering::Less=>todo!(),
// E.g. curr=2018-01-14 and day=14
Ordering::Equal=>todo!(),
// E.g. curr=2018-01-14 and day=12
Ordering::Greater=>todo!(),
}
}
}
}
}

...其中 Less 和 Equal 分支非常简单：

matchself{
/* ... */
Rule::DayOfMonth(day)=>{
matchcurr.day().cmp(day){
// E.g. curr=2018-01-14 and day=16
Ordering::Less=>curr+Span::new().days(day-curr.day()),
// E.g. curr=2018-01-14 and day=14
Ordering::Equal=>curr,
// E.g. curr=2018-01-14 and day=12
Ordering::Greater=>todo!(),
}
}
}

那么 => Ordering::Greater 呢？嗯，我们可以提供一个确切的解决方案：

// E.g. curr=2018-01-14 and day=12
Ordering::Greater=>{
// 2018-01-14 -> 2018-02-14
letdst=curr+Span::months(1);
// 2018-02-14 -> 2018-02-01
letdst=dst.first_of_month().unwrap();
// 2018-02-01 -> 2018-02-12
dst+Span::days(*day-1)
}

...但由于低估是合法的，我们不妨选择更简单的方法：

Ordering::Greater=>curr.last_of_month().tomorrow().unwrap(),

给定 curr=2018-01-14 和 day=12，该函数将建议跳到 2018-02-01，然后在下一次迭代中，我们将访问 Less 分支，最终得到 2018-02-12。有点低效，但合法。

明白了，你没有考虑到不存在的日期，例如 2018-02-31 ！！！

调整领结 实际上，这样的日子可以正常工作，但也有些低效，例如：

Rule::DayOfMonth(31)
.next(date("2018-02-14"))

...会说 2018-03-03——这是合法的，因为实际的下一次发生是在 2018-03-31 上，对于 2018-03-31 来说，2018-03-03 是一个有效的低估。

请注意，理想情况下我们的函数_会_返回 2018-03-31，但它不必这样做。

好的，我们有 day-of-week，我们有 day-of-month——是时候进行条件判断了！

Yield Me Maybe

我们需要支持两种类型的布尔运算符，or 和 and。 or 用于组合同一参数的值，而 and 用于跨参数组合：

FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10;DTSTART=20180101

(and
 (or (day-of-week Monday) (day-of-week Tuesday))
 (day-of-month 10))

...或者，没那么 LISP-y：

FREQ=DAILY;BYDAY=MO,TU;BYMONTHDAY=10;DTSTART=20180101

(day-of-week(Monday) or day-of-week(Tuesday)) and day-of-month(10)

那么 day-of-week(Monday) or day-of-week(Tuesday) 是什么意思？悲观地看，它就像：

if day-of-week(Monday) == 0 or day-of-week(Tuesday) == 0:
  return 0
else
  return +1s

...也就是说，我们慢慢地前进，寻找任何返回零的函数。我们知道以秒为单位前进是合法的，只是不是最佳的，所以现在的问题变成了——我们如何做得更好？

我们的函数具有这个很好的属性：

if:
  f(x) = y
then, for t >= 0 && x + t <= y:
  f(x + t) = y

直观地说——如果 (day-of-week Friday 2018-01-01) 返回 2018-01-05，那么当从 2018-01-01 询问到包括 2018-01-05 时，它会说相同的话：

(day-of-week Friday 2018-01-01) = 2018-01-05
(day-of-week Friday 2018-01-02) = 2018-01-05
(day-of-week Friday 2018-01-03) = 2018-01-05
(day-of-week Friday 2018-01-04) = 2018-01-05
(day-of-week Friday 2018-01-05) = 2018-01-05

这意味着 f(x) or g(x) 对应于 min(f(x), g(x))，我们可以通过执行以下操作来估计：

FREQ=DAILY;BYDAY=MO,TU;DTSTART=20180103

since 2018-01-03 is Wednesday, we'd expect for the next ocurrences to be:
-> 2018-01-08 (Monday, since it comes before the next Tuesday)
-> 2018-01-09 (Tuesday, since it comes before the next Monday)
-> 2018-01-15 (Monday, ...)
-> [...]

这可以归结为以下可爱的代码片段：

enumRule{
/* ... */
Or(Vec<Self>),
}
implRule{
fnnext(&self,curr:Date)->Date{
matchself{
/* ... */
Rule::Or(rules)=>{
rules
.iter()
.map(|rule|rule.next(curr))
.min()
.unwrap_or(curr)
}
}
}
}

相反，and = max，原因类似：如果 f(x) 说它在某个日期 A 之前不会有效，并且 g(x) 说它在某个日期 B 之前不会有效，那么两者至少在 max(A, B) 之前都不会有效。这并不一定意味着这两个规则_在_ max(A, B) 处都有效，例如：

FREQ=DAILY;BYDAY=MO;BYMONTHDAY=10;DTSTART=20180101

(and
  (day-of-week Monday)
  (day-of-month 10))
Given 2018-01-03, we'll evaulate:
  (day-of-week Monday 2018-01-03)
  =