如何优化你的 Rust 程序以降低速度：受图灵机新结果的启发

编写一个在宇宙终结后才完成的简短程序

Carl M. Kadie Carl M. Kadie · Follow 20 min read · Apr 1, 2025

Share Source: https://openai.com/dall-e-2/. All other figures from the author.

另有：本文的 Python 版本。

每个人都在谈论如何让 Rust 程序更快 [1, 2, 3]，但如果我们追求相反的目标呢？ 让我们探索如何让它们更慢——慢得离谱。 在此过程中，我们将研究计算的本质、内存的作用以及难以想象的大数字的规模。

我们的指导性挑战是：编写运行时间极长的短小的 Rust 程序。

为此，我们将探索一系列规则集——每个规则集通过对停止、内存和程序状态的约束来定义允许我们编写的程序类型。 这个序列不是一个递进的过程，而是一系列视角的转变。 每个规则集都有助于揭示简单的代码如何能延长时间。

以下是我们将会研究的规则集：

  1. 随心所欲 — 无限循环
  2. 必须停止，有限内存 — 嵌套的、固定范围的循环
  3. 无限的、零初始化的内存 — 5 状态图灵机
  4. 无限的、零初始化的内存 — 6 状态图灵机 (>10↑↑15 步)
  5. 无限的、零初始化的内存 — 纯 Rust (计算 10↑↑15 而无需图灵机模拟)
  6. 奖励 — 快速(er)运行慢速程序

旁注：10↑↑15 不是拼写错误或双重指数。 这是一个非常大的数字，以至于“指数”和“天文数字”都无法描述它。 我们将在规则集 4 中定义它。

我们从最宽松的规则集开始。 从那里，我们将逐步更改规则，以了解不同的约束如何影响长时间运行的程序的外观——以及它们能教会我们什么。

规则集 1：随心所欲 — 无限循环

我们从最宽松的规则开始：程序不需要停止，可以使用无限内存，并且可以包含任意代码。

如果我们的唯一目标是永远运行，那么解决方案是立竿见影的：

fn main() {  loop {}}

这个程序很短，使用的内存可以忽略不计，并且永远不会完成。 它以最字面的方式满足了挑战——永远不做任何事情。

当然，它并没有什么意义——它什么也不做。 但它给了我们一个基线：如果我们移除所有约束，无限的运行时是微不足道的。

在下一个规则集中，我们将引入我们的第一个约束：程序最终必须停止。 让我们看看在新要求下，我们能将运行时间延长到什么程度——仅使用有限内存。

规则集 2：必须停止，有限内存 — 嵌套的、固定范围的循环

如果我们想要一个比宇宙存在时间更长_然后停止_的程序，这很容易。 只需编写四个嵌套循环，每个循环都在从 0 到 2¹²⁸−1 的固定范围内计数：

fn slow_enough() {  for a in 0..u128::MAX {    for b in 0..u128::MAX {      for c in 0..u128::MAX {        for d in 0..u128::MAX {          if d % 1_000_000_000 == 0 {            println!("{} {} {} {}", a, b, c, d);          }        }      }    }  }}

你可以看到这个程序在 u128::MAX × u128::MAX × u128::MAX × u128::MAX 步之后停止。 也就是 340,282,366,920,938,463,463,374,607,431,768,211,455⁴ 步，或大约 10¹⁵⁴ 步。 并且——忽略 println!——这个程序仅使用少量堆栈内存来保存其四个 u128 循环变量——仅 64 字节。

我的台式计算机以大约每秒 10 亿步的速度运行此程序的发布版本。 但假设它能以 普朗克速度 (物理学中最小的有意义的时间单位) 运行。 那将是大约每年 10⁵⁰ 步——因此完成需要 10¹⁰⁴ 年。

当前的宇宙学模型估计 宇宙的热寂 将在 10¹⁰⁰ 年后发生，因此我们的程序将比宇宙的预计寿命长大约 10,000 倍。

旁注：关于在宇宙终结后运行程序的实际问题不在本文的讨论范围内。

为了增加余量，我们可以使用更多内存。 与其使用 64 字节的变量，不如使用 64 GB——这大约是你在配置良好的个人计算机中能找到的。 那是多 10⁹ 倍的内存，这给了我们大约 4 × 10⁹ 个变量而不是 4 个。 如果每个变量都在完整的 u128 范围内迭代，则总步数将大约为 u128::MAX^(4×10⁹)，或大约 10^(1650 亿) 步。 以普朗克速度——大约每年 10⁵⁰ 步——这相当于 10^(1650 亿 − 50) 年的计算时间。

我们能做得更好吗？ 好吧，如果我们允许一个不切实际但有趣的规则更改，我们就能做得更好得多。

规则集 3：无限的、零初始化的内存 — 5 状态图灵机

如果我们允许无限内存——只要它完全以零开始初始化呢？

旁注： 为什么我们不允许无限的、任意初始化的内存？ 因为它使挑战变得微不足道。 例如，你可以在内存中很远的地方用 0x01 标记一个字节——例如，在位置 10¹²⁰ 处——并编写一个微小的程序，该程序只需扫描直到找到它。 该程序将花费极长的时间来运行——但这并没有什么意义。 缓慢已融入数据中，而不是代码中。 我们追求的是更深层次的东西：小型的程序可以从简单、统一的起始条件下生成自己的长时间运行。

我的第一个想法是使用内存以二进制方式向上计数：

011011100101110111...

我们可以做到这一点——但我们如何知道何时停止？ 如果我们不停止，我们就会违反“必须停止”规则。 那么，我们还能尝试什么呢？

让我们从计算机科学之父 Alan Turing 那里获得灵感。 我们将编程一个简单的抽象机器——现在称为 图灵机 ——在以下约束下：

位于无限磁带上的读/写头。

enum State { A, B, C, D, E, H }

我们可以将完整的图灵机程序表示为转换表。 这是一个我们将逐步执行的示例。

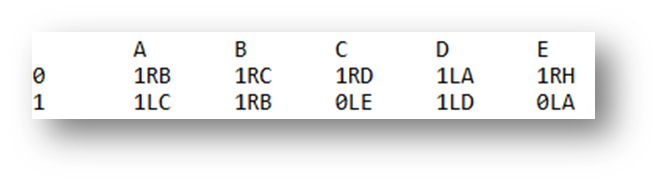一个 5 状态图灵机转换表。

现在我们已经定义了机器，让我们看看它如何随时间变化。

我们将时间上的每个时刻——机器和磁带的完整配置——称为 步。 这包括当前的磁带内容、磁头位置和机器的内部状态(如 A、B 或 H)。

下面是 第 0 步。 磁头指向磁带上的 0，机器处于 状态 A。

查看程序表中的 第 0 行，A 列，我们找到指令 1RB。 这意味着：

第 0 步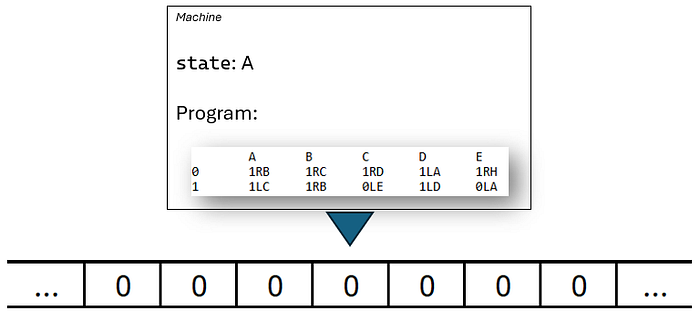： 这使我们进入 第 1 步：

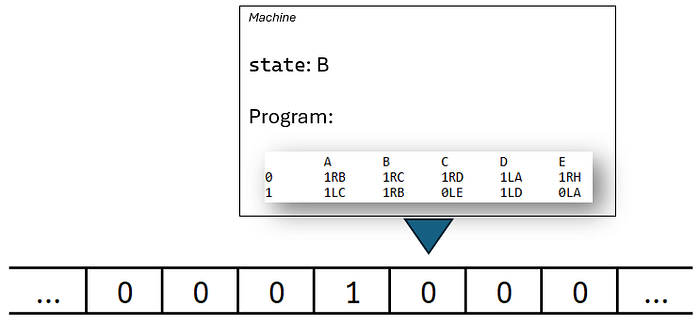机器现在处于 状态 B，指向下一个磁带单元格(同样是 0)。

如果我们让这个图灵机继续运行会发生什么？ 它将运行整整 47,176,870 步 ——然后停止。

这个数字本身就令人惊讶，但看到完整的运行过程使其更加具体。 我们可以使用 时空图 可视化执行过程，其中每一行显示磁带在单个步骤中的状态，从顶部(最早)到底部(最新)。 在图像中：

冠军 5 状态图灵机的时空图。 它在停止之前运行 47,176,870 步。 每一行显示磁带在单个步骤中的状态，从顶部开始。 橙色表示 1，白色表示 0。

在 2023 年，一个由业余研究人员组成的在线小组通过 bbchallenge.org 组织，证明这是最终停止的 运行时间最长的 5 状态图灵机。

旁注：他们使用 Coq 证明助手正式验证了他们的证明。 如果你对形式验证和 Rust 感兴趣，请参阅 完美且自动地检查 AI 生成的代码 和 使用 Dafny 在 Towards Data Science 中正式验证 Rust 算法的九条规则。

想看看这个图灵机的运行情况吗？ 你可以在这个 像素完美的视频 中观看完整的 4700 万步执行过程：

或者使用 Busy Beaver Blaze web app 直接与之交互：

Busy Beaver Blaze 使用这个由 Rust 驱动的交互式 WASM 模拟器探索图灵机和忙碌的海狸。carlkcarlk.github.io

视频生成器和 web app 是 busy-beaver-blaze 的一部分，它是本文随附的开源 Rust 项目。 有关将 Rust 代码移植到 WASM 的提示，请参阅我在 Towards Data Science 中的 在浏览器中运行 Rust 的九条规则。

很难相信如此小的机器可以运行 4700 万步 并仍然停止。 但它变得更加令人震惊：bbchallenge.org 的团队发现了一个 6 状态机器，其运行时间如此之长，甚至无法用普通指数来书写。

规则集 4：无限的、零初始化的内存 — 6 状态图灵机 (>10↑↑15 步)

截至撰写本文时，人类已知的运行时间最长(但仍然停止)的 6 状态图灵机是：

  A  B  C  D  E  F0  1RB 1RC 1LC 0LE 1LF 0RC1  0LD 0RF 1LA 1RH 0RB 0RE

这是一个显示其 前 10 万亿步 的视频：

你可以在 web app 中交互式运行它。

那么，如果我们有耐心——极度耐心——这个图灵机将运行多久？ 超过 10↑↑15，其中 “10 ↑↑ 15” 表示：

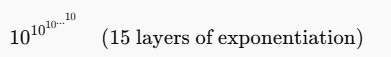
这 不是 与 10¹⁵ 相同 (这只是一个普通指数)。 相反：

Pavel Kropitz 于 2022 年 5 月 30 日宣布了这台 6 状态机器。 Shawn Ligocki 有一篇 很棒的文章 解释了他和 Pavel 的发现。 为了证明这些机器运行如此之长然后停止，研究人员使用了分析和自动化工具的组合。 他们没有模拟每个步骤，而是识别出可以证明的重复结构和模式——使用正式的、机器验证的证明——最终导致停止。

到目前为止，我们一直在谈论图灵机——特别是，最终停止的最长已知 5 状态和 6 状态机器。 我们将 5 状态冠军运行到完成并构建可视化来探索其行为。 但是，它是有 5 个状态的最长停止机器的发现——以及 6 状态竞争者的识别——来自广泛的研究和形式证明，而不是来自逐步运行它们。

也就是说，我构建了一个基于 Rust 的可视化工具，可以模拟这些机器数万亿步——足以探索它们的早期行为。 但即使 10 万亿步 与 6 状态机器的完整运行时间相比，也只是大海捞针。 并且像我们所做的那样运行它并不能使我们更接近于理解_为什么_它运行如此之长。

旁注： Rust 将图灵机 “解释” 到某个点——读取它们的转换表并逐步应用规则。 你也可以说它 “模拟” 了它们，因为它完全重现了它们的行为。 我避免使用 “模拟” 这个词：模拟的大象不是大象，但模拟的计算机_是_计算机。

回到我们的中心挑战： 我们想了解是什么使一个短程序运行很长时间。 与其分析这些图灵机，不如构建一个 Rust 程序，其 10↑↑15 运行时间在设计上是明确的。

规则集 5：无限的、零初始化的内存 — 纯 Rust (计算 10↑↑15 而无需图灵机模拟)

我们的挑战是编写一个至少运行 10↑↑15 步的小型 Rust 程序，使用任意数量的零初始化内存。

为了实现这一点，我们将以一种保证程序至少需要那么多步骤的方式计算 10↑↑15 的值。 ↑↑ 运算符称为 tetration —— 回顾一下规则集 4，↑↑ 堆叠指数：例如，10↑↑3 表示 10^(10^10)。 这是一个增长极快的函数。 我们将从头开始编程它。

与其依赖内置运算符，不如从第一原理定义 tetration：

每一层都建立在它下面的一层之上，仅使用零初始化内存和就地更新。

我们将从基础开始——从所有操作中最简单的操作开始：increment。

增量

这是我们对 increment 的定义：

fn increment(increment_acc: &mut BigUint) {  *increment_acc += 1u32;}

例如：

let mut b = BigUint::from(4u32);print!("++{b}\t= ");increment(&mut b);assert_eq!(b, BigUint::from(5u32));println!("{b}");

输出：

++4   = 5

我们正在使用 BigUint，这是 num-bigint crate 中的一种类型，表示任意大的无符号整数——仅受可用内存的限制。 在本文中，我们将假装内存是无限的。

为了保持简单并与我们的规则保持一致，我们将自己限制为仅对 BigUint 执行几个操作：

我们不允许复制、克隆或除增量和减量之外的算术运算。 所有工作都在本地进行——没有临时值。

我们的计算层中的每个函数都遵循一致的结构：它就地更新一个可变累加器。 大多数函数还接受一个输入值 a，但 increment ——作为最简单的——不接受。 我们给累加器提供描述性名称，如 increment_acc、add_acc 等，以使每个操作清晰，并为后面的部分做准备，在后面的部分中，多个累加器将一起出现。

加法

定义了 increment 之后，我们接下来将加法定义为重复增量。

fn add(a: u32, add_acc: &mut BigUint) {  for _ in 0..a {    // 我们手动内联 `increment`，以保持我们的工作明确。    *add_acc += 1u32;  }}

该函数通过递增 add_acc a 次，将 a 添加到 add_acc。

旁注： 你可能想知道为什么 add 不只是调用我们的 increment 函数。 我们可以这样写——但我们故意手动内联每个级别。 这使所有循环都可见，使控制流显式，并帮助我们准确地推断出函数的工作量。

让我们使用我们新的 add 函数：

let a = 2;let mut b = BigUint::from(4u32);print!("{a} + {b}\t= ");add(a, &mut b);assert_eq!(b, BigUint::from(6u32));println!("{b}");

输出：

2 + 4   = 6

即使 BigUint 支持直接加法，我们也不使用它。 我们故意以最原始的级别工作——按 1u32 递增——以保持逻辑简单和缓慢，并使工作量显式。

与 increment_acc 一样，我们就在本地更新 add_acc，没有复制或临时值。 我们使用的唯一操作是 += 1u32，重复 a 次。

接下来，我们定义 乘法。

乘法

有了加法，我们现在可以将乘法定义为重复加法。 这是该函数：

fn multiply(a: u32, multiply_acc: &mut BigUint) {  let mut add_acc = BigUint::ZERO;  for () in multiply_acc.count_down() {    for _ in 0..a {      add_acc += 1u32;    }  }  *multiply_acc = add_acc;}

这会将 a 乘以 multiply_acc 的值，方法是为 multiply_acc 可以递减的每次将 a 添加到 add_acc 一次。 然后它将结果存储回 multiply_acc 中。

让我们使用 multiply：

let a = 2;let mut b = BigUint::from(4u32);print!("{a} * {b}\t= ");multiply(a, &mut b);assert_eq!(b, BigUint::from(8u32));println!("{b}");

输出：

2 * 4   = 8

与之前的函数一样，我们都在本地执行计算，不使用复制、临时值或内置算术运算。 允许的唯一操作是递增、递减和零比较。

你可能想知道这一行在做什么：

for () in multiply_acc.count_down()

因为 BigUint 不支持像 for _ in 0..n 这样的循环，所以我们使用自定义方法 .count_down()。 只要值非零，它就会循环，每次将其递减 1。 即使 n 任意大，这也能为我们提供受控的、就地的 “循环 n 次” 版本。

我们已经通过重复加法构建了乘法。 现在是更进一步的时候了：求幂。

求幂

我们将求幂定义为重复乘法。 与之前一样，我们将就地执行每个乘法步骤，仅使用零初始化内存。

这是该函数：

fn exponentiate(a: u32, exponentiate_acc: &mut BigUint) {  assert!(    a > 0 || *exponentiate_acc != BigUint::ZERO,    "0^0 is undefined"  );  let mut multiply_acc = BigUint::ZERO;  multiply_acc += 1u32;  for () in exponentiate_acc.count_down() {    let mut add_acc = BigUint::ZERO;    for () in multiply_acc.count_down() {      for _ in 0..a {        add_acc += 1u32;      }    }    multiply_acc = add_acc;  }  *exponentiate_acc = multiply_acc;}

这会将 a 提高到 exponentiate_acc 的幂，仅使用递增、递减和循环控制。 我们使用单个增量将 multiply_acc 初始化为 1——因为从零开始重复乘法将一无所获。 然后，对于 exponentiate_acc 可以递减的每次，我们将当前结果 (multiply_acc) 乘以 a。 与之前的层一样，我们直接内联乘法逻辑，而不是调用 multiply 函数——因此控制流和步数计数保持完全可见。

这是我们使用 exponentiate 的方式：

let a = 2;let mut b = BigUint::from(4u32);print!("{a}^{b}\t= ");exponentiate(a, &mut b);assert_eq!(b, BigUint::from(16u32));println!("{b}");

输出：

2^4   = 16

旁注： 并且 += 1u32 被调用了多少次？ 显然至少 2⁴ 次——因为我们的结果是 2⁴，并且我们通过从零开始递增来实现它。 更准确地说，增量数是： • 1 个增量——将 multiply_acc 初始化为 1。然后我们循环 4 次，并且在每个循环中，我们使用重复加法将 multiply_acc 的当前值乘以 a = 2： • 2 个增量——对于 multiply_acc = 1，添加 2 一次 • 4 个增量——对于 multiply_acc = 2，添加 2 两次 • 8 个增量——对于 multiply_acc = 4，添加 2 四次 • 16 个增量——对于 multiply_acc = 8，添加 2 八次 总共是 1 + 2 + 4 + 8 + 16 = 31 个增量，即 2⁵-1。 通常，对 increment 的调用次数将呈指数增长，但该数与我们正在计算的指数不同。

定义了求幂之后，我们就可以到达我们塔的顶部了：tetration。

Tetration

这是该函数：

fn tetrate(a: u32, tetrate_acc: &mut BigUint) {  assert!(a > 0, "we don’t define 0↑↑b");  let mut exponentiate_acc = BigUint::ZERO;  exponentiate_acc += 1u32;  for () in tetrate_acc.count_down() {    let mut multiply_acc = BigUint::ZERO;    multiply_acc += 1u32;    for () in exponentiate_acc.count_down() {      let mut add_acc = BigUint::ZERO;      for () in multiply_acc.count_down() {        for _ in 0..a {          add_acc += 1u32;        }      }      multiply_acc = add_acc;    }    exponentiate_acc = multiply_acc;  }  *tetrate_acc = exponentiate_acc;}

这会计算 a ↑↑ tetrate_acc，这意味着它会重复地将 a 自乘，tetrate_acc 次。

对于 tetrate_acc 的每次递减，我们都会对当前值进行求幂。 我们再次内联整个 exponentiate 和 multiply 逻辑，一直到重复增量。

这是我们使用 tetrate 的方式：

let a = 2;let mut b = BigUint::from(3u32);print!("{a}↑↑{b}\t= ");tetrate(a, &mut b);assert_eq!(b, BigUint::from(16u32));println!("{b}");

输出：

2↑↑3   = 16

正如预期的那样，这会计算 2^(2^2) = 16。 你可以 自己在 Rust Playground 上运行它。

我们还可以在 10↑↑15 上运行 tetrate。 它会开始运行，但它不会在我们的一生中停止——甚至在宇宙的生命周期内也不会停止：

let a = 10;let mut b = BigUint::from(15u32);print!("{a}↑↑{b}\t= ");tetrate(a, &mut b);println!("{b}");

让我们将这个 tetrate 函数与我们在之前的规则集中找到的进行比较。

规则集 1：随心所欲 — 无限循环

回想一下我们的第一个函数：

fn main() {  loop {}}

与这个无限循环不同，我们的 tetrate 函数最终会停止——尽管不会很快。

规则集 2：必须停止，有限内存 — 嵌套的、固定范围的循环

回想一下我们的第二个函数：

fn slow_enough() {  for a in 0..u128::MAX {    for b in 0..u128::MAX {      for c in 0..u128::MAX {        for d in 0..u128::MAX {          if d % 1_000_000_000 == 0 {            println!("{} {} {} {}", a, b, c, d);          }        }      }    }  }}

slow_enough 和我们的 tetrate 函数都包含固定数量的嵌套循环。 但是 tetrate 在一个重要方面有所不同：循环迭代的数量随输入值而增长。 在 slow_enough 中，每个循环都从 0 运行到 u128::MAX —— 一个硬编码的界限。 相比之下，tetrate 的循环边界是动态的——它们随着计算的每一层呈指数增长。

规则集 3 和 4：无限的、零初始化的内存 — 5 状态和 6 状态图灵机

与图灵机相比，我们的 tetrate 函数具有明显的优势：我们可以直接看到它将调用 += 1u32 超过 10↑↑15 次。 更好的是，我们还可以通过构造看到它停止了。

图灵机提供的是一个更简单、更通用的计算模型——以及可能更原则性的定义，即什么算作 “小型程序”。

到此为止，我们为使程序变慢所做的努力就告一段落了。 在结论中，我们将总结并反思这些意外之处。

但在此之前，还有一个转折：让我们让一些慢速程序运行得更快。

奖励：规则集 6 — 运行快(速)慢速程序

在经过所有努力之后，故意放慢速度，这里有一个惊喜：让我们看看使 Rust 程序运行更快的技术。

一些简单但有效的优化使图灵机可视化工具的速度足以使用像素合并(我稍后将定义的一个术语)渲染 10 万亿步。

即使是 Rust WASM 版本 —— 现在是 [bbchallenge.org](https://medium.com/@carlmkadie/</bb