Collatz蚂蚁及其序列的相似性

这是之前一篇文章 (Repo)的简要延续，该文章介绍了基于Langton’s Ant的 Collatz 序列可视化方法。

Collatz蚂蚁基于collatz 函数：

\[f(n) = \begin{cases} n/2 & \text{if} \quad n \equiv 0 \quad (\text{mod}, 2) \\ 3n + 1 & \text{if} \quad n \equiv 1 \quad (\text{mod}, 2) \\ \end{cases}\]

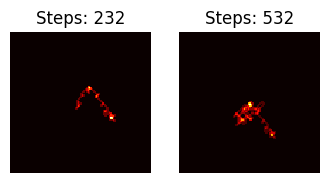
此外，如果 $n \equiv 0 , (\text{mod}, 2)$，蚂蚁顺时针旋转 90º，否则蚂蚁逆时针旋转 90º。在这两种情况下，单元格的状态都会翻转，并且蚂蚁向前移动一个单位。这个过程重复直到 $n = 1$。以下动画展示了一个例子：

从 $n = 10^{40}$ 到 $n = 10^{40} + 20$ 的连续轨迹示例。

虽然这种表示方法很有趣，但状态的翻转最终可能导致模糊的场景1，在这些场景中，轨迹似乎通过省略彼此相似。

鉴于此，下图对应于蚂蚁的“景观”（最终快照），在相同轨迹下不进行状态翻转，并显示了各自的停止时间。 这仅仅是通过将蚂蚁经过的每个坐标的计数加 $+1$2来实现的。

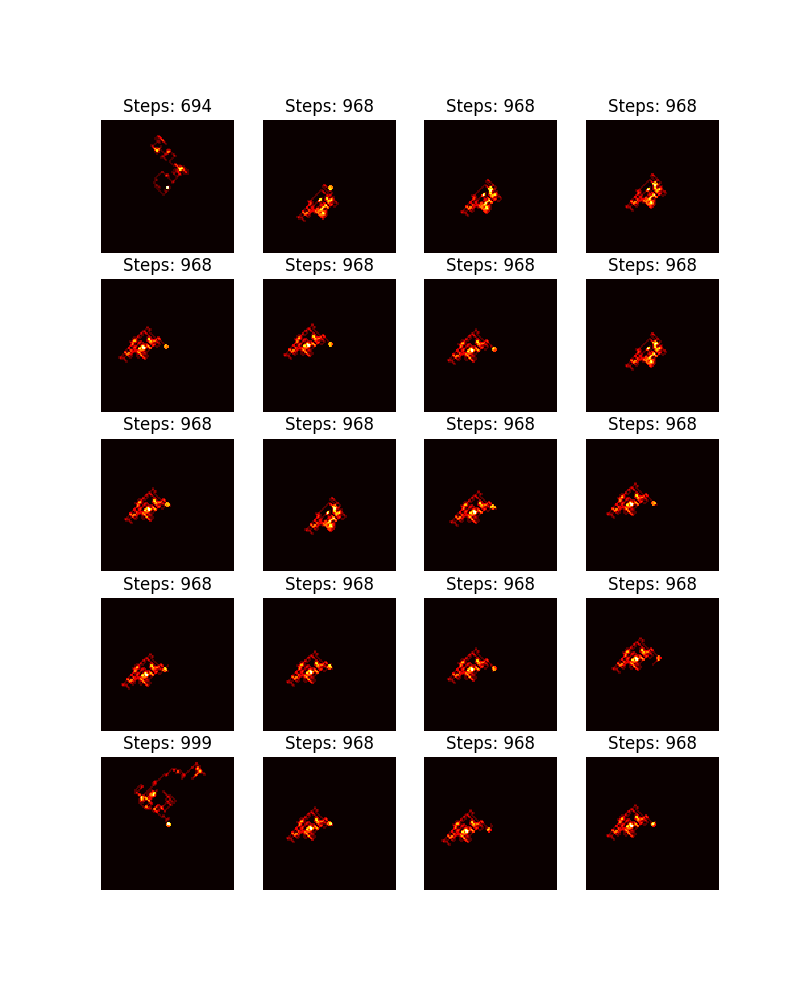
其他一些例子

从 $n = 2$ 到 $n = 102$ 的前 100 个数字。

从 $n = 10^{9}$ 到 $n = 10^{9} + 100$。

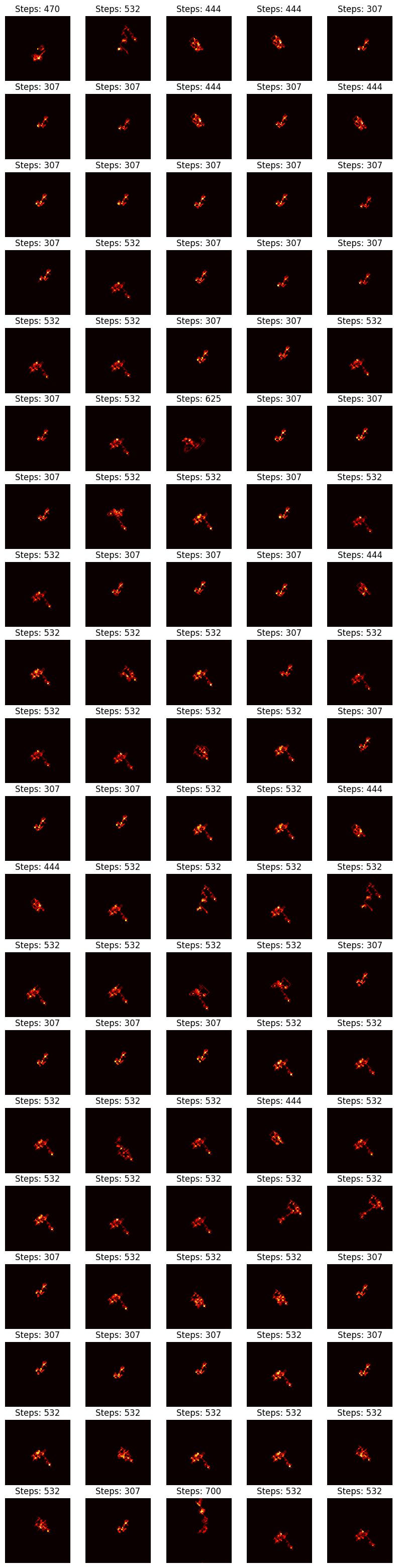
从 $n = 10^{20}$ 到 $n = 10^{20} + 100$。

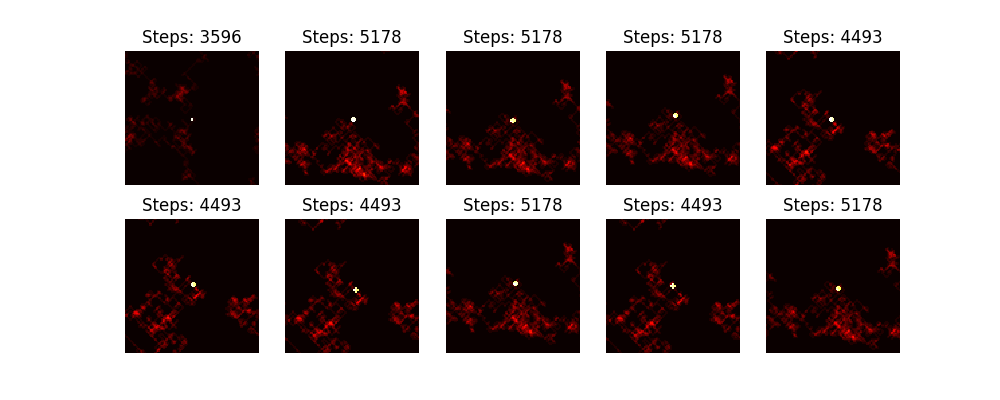
从 $n = 10^{200}$ 到 $n = 10^{200} + 10$。

一些有趣的发现

• 非常相似的“景观”具有相同的停止时间（或相似的停止时间）3，但反之则不然。反之不成立的一个例子是此比较中 $n = 10^{20} + 1$ (第一行，第二列) 和 $n = 10^{20} + 16$ (第四行，第二列) 的情况，它们的停止时间都是 532。

如果我们检查这两个轨迹之间的相似性：

import numpy as np
import mpmath
def collatz_seq(n):
  seq = []
  while n != 1:
    seq.append(n)
    if n % 2 == 0:
    	n /= 2
    else:
    	n = 3*n + 1
  return seq
mpmath.mp.dps = 22
n1 = mpmath.mpf("1e20") + 1
n2 = mpmath.mpf("1e20") + 16
len(np.intersect1d(collatz_seq(n1), collatz_seq(n2)))

Output: 142

如果对 $n = 10^{20} + 16$ 和 $n = 10^{20} + 20$ 执行相同的操作，它们具有相似的“景观”和相同的停止时间，我们会得到：

Output: 527

• 此外，如果我们现在查看子轨迹收敛的一个例子，在本例中，每个子轨迹相差 5 步，我们可以看到“景观”彼此非常相似，只是旋转方向不同 (似乎总体旋转了 90º)3。 这当然是由于蚂蚁在最初的 5 步内进行了重新定向所致。

$n = 18750000000000000004$ 和 $n = 10^{20} + 16$ 的例子，前者是在后者的 5 个归约步骤后找到的。

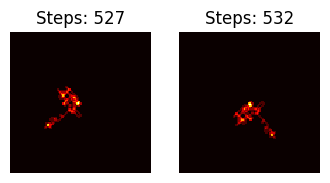
现在相差 100 步， “景观”看起来仍然非常相似，但旋转了 180º。

相差 200 步，“景观”开始失去一些彼此相关的细节。

相差 300 步，现在两个“景观”之间只有少数大规模的特征是相同的。

返回

x.com | GitHub