经过 20 年，全局最优的 Boggle 棋盘

激动人心的消息！这是可能获得的最佳 Boggle 棋盘：

Photo of the best possible Boggle board: P E R S / L A T G / S I N E / T E R S

Boggle 是一种单词搜索游戏。您可以通过连接相邻的字母来组成单词，包括沿对角线连接。较长的单词得分更高。这个棋盘上的好词包括 STRANGERS 和 PLASTERING。在您花费三分钟尝试找到尽可能多的单词后，您会被电脑在这方面的能力所折服。

使用 ENABLE2K word list，这个棋盘上有 3,625 points，来自 1,045 个单词。这个棋盘比任何其他棋盘都获得更高的分数。尝试任何其他字母组合，您都会得到较低的分数。虽然我 早就怀疑 这个棋盘是获胜者，但我现在通过穷举搜索证明了这一点。

很多人 之前都搜索过 高分棋盘，但从未有人构建过计算证明来证明他们找到了最好的棋盘。这是 Boggle 的一项新的、首创的成果。

要了解为什么这很有趣，让我们回到 20 世纪 80 年代。

高分 Boggle 和局部最优

随着 Apple II (1977) 和 IBM PC (1981) 的发布，电脑变得可以被爱好者使用，包括文字游戏爱好者。1982 年，Alan Frank 在 Word Ways 杂志上发表了一篇名为 High-Scoring Boggle 的短文。这是我找到的关于 Boggle 最大化的最早的作品，它说明了为什么这是一个难题。

这是他写的：

Scan of type-written article from 1982 showing the board G N I S / E T R P / S E A C / D B L S and stating: With the aid of a computer, Steve Root and I have discovered that the array at the right is very likely the highest-scoring one for words from the Official Scrabble Players Dictionary; a score of 2047 was achieved.

这篇文章接着列出了 769 个单词，总计 2,047 分。您可以使用第五版 OSPD 在此处浏览该棋盘上的单词：gnisetrpseacdbls。（由于添加了新单词，它已增加到 2,226 分。）

文章没有解释 Alan 和 Steve 是如何提出这个特定棋盘的，但我怀疑他们使用了 hill climbing 过程。这个想法很简单：从一个随机棋盘开始，找到它的分数。调整一个字母，看看分数是否提高。如果是，则保留它。如果不是，则放弃更改。重复直到停滞。您最终会得到一个高分棋盘。

在 1982 年编写 Boggle 解算器并找到这个棋盘是一项真正的成就。但不幸的是，对于 Alan 和 Steve 来说，他们的棋盘不是“得分最高的棋盘”。它甚至还差得很远。本文顶部的棋盘使用 OSPD5 获得了 3,736 points，远远超过他们的。

那么出了什么问题？如果没有他们的代码，很难说，但我有一个预感。爬山法的克星是局部最大值：

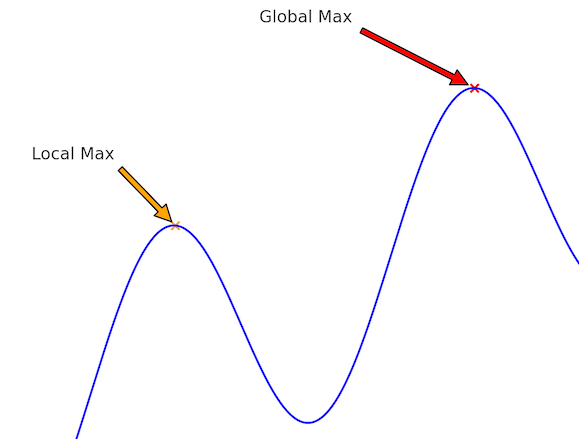
Chart showing a local and global maximum

爬山法很容易找到局部最大值，而不是全局最大值。大概 Alan 和 Steve 的棋盘是局部最优的，并且小的更改无法改进它。但仍然存在一个更好的棋盘，您只需先下降您的小山，然后才能爬上更高的山。局部优化总是会以这种方式失败。您可能只是在错误的社区中寻找。

更深入的搜索

我在 2004 年编写了我的第一个 Boggle Solver，并迅速 got interested 使用爬山法和模拟退火来找到高分棋盘。我 wasn’t the only one。

2000 年代的 Boggle 程序比 1982 年的 Alan 和 Steve 的程序有一些主要优势。内存便宜得多，CPU 快得多，互联网使得获取单词列表容易得多。

这意味着您可以进行“更深入”的搜索：

使用 process like this，我发现，无论我从哪个棋盘开始，我总是会得到少数几个高分棋盘之一，包括我们最喜欢的 3,625 分的棋盘。

这表明这个棋盘可能只是全局最大值。但是，我们可能仍然会像以前一样陷入相同的陷阱。真正的全局最优可能只是很难以这种方式找到。

唯一 for sure 的方法是通过穷举搜索。不幸的是，至少乍一看，这似乎完全不可能。

穷举搜索的不可能性

可能存在的 Boggle 棋盘数量非常庞大。有多少？如果任何字母都可以出现在任何位置，那么大约有

26^16/8 = 5,451,092,862,428,609,257,472 = 5.45*10^21

个可能的棋盘。（因子 8 来自对称性；并非所有棋盘都可以用真正的 Boggle 骰子滚动，但这是 within an order of magnitude。）

可以使用 Trie data structure very quickly 找到 Boggle 棋盘上的所有单词。在我的 M2 Macbook 上，我可以为大约 200,000 个棋盘/秒评分。尽管如此，按照这个速度，测试每个棋盘大约需要 8 亿年！

幸运的是，有一种更聪明的方法来构建搜索。

分支定界

要查看的棋盘太多了。即使枚举所有这些棋盘也会太慢。相反，我们需要将棋盘组合成一个“棋盘类”。然后，我们可以计算每个类中得分最高的棋盘的 upper bound。如果此上限低于 3625，我们可以丢弃整个类，而无需测试其中的任何单个棋盘。如果不是，我们需要拆分类并重试。

这种技术被称为 Branch and Bound，它最初是在 20 世纪 60 年代开发的。B&B 更多的是一种策略而不是具体的算法，并且留下了很多细节需要填写。将此方法应用于 Boggle 的聪明之处在于：

  1. 将 Boggle 棋盘空间划分为 board classes 的适当方法
  2. 一种 upper bound，该上限的计算速度很快，但仍然相当“tight”
  3. 一种 split board classes 并计算其上限的方法，而无需重复工作

“棋盘类”可能包含数万亿个单独的棋盘。一个例子是具有特定辅音/元音模式的棋盘。大约有 2^16/8=8192 种可能的辅音/元音模式——远少于棋盘的数量。您可以想象很容易排除所有辅音或所有元音的棋盘。不过，其他模式要困难得多。（我的搜索并没有完全使用辅音和元音，这只是一个说明。）有关棋盘类的更多信息，请阅读 this post。

第二个和第三个想法需要开发一种 somewhat novel tree structure 专为 Boggle 设计。这些“sum/choice”树使得计算上限和拆分棋盘类都非常有效。您可以在 this post 中查看这些树的示例并了解它们的工作原理。

如果您想了解有关这些算法和数据结构的更多信息，我鼓励您在自己的机器上 run the code 并阅读我之前的一些博客文章，这些文章更详细地介绍了这些算法和数据结构：

结果

我在 3x3 和 3x4 Boggle 上开发和测试了搜索算法，这些是 much easier problems。然后我在 4x4 Boggle 上运行了它。

使用 Google Cloud 上的 192 核 c4，检查大约 100 万个 4x4 棋盘类（约 23,000 个 CPU 小时）花费了大约 5 天的时间。这大约是 1,200 美元的计算费用。这很多，但并不是一个疯狂的数字。（幸运的是，我在 BigTech 中有一个朋友，他们有多余的 CPU。）

结果是使用 ENABLE2K word list 获得 3500+ 分的所有 Boggle 棋盘的列表（直到对称性）。共有 32 个。以下是前五个：

您可以在 here 看到其余部分。这些棋盘富含 -ING、-ER、-ED 和 -S 等高价值结尾。

排名靠前的棋盘都是我之前通过爬山法发现的。

我们从这个问题中学到了什么？

问题和答案

使用了哪些工具？

代码是 C++（用于性能关键部分）和 Python（用于其他所有内容）的混合。它们使用 pybind11 粘合在一起，我是它的忠实拥护者。

如果您想运行代码或了解更多信息，请查看 GitHub repo。

如果存在错误怎么办？

我会哭的。😭 虽然我永远不会排除出现错误的可能性，但有几个理由相信这个计算证明是正确的：

  1. 它与在 2x2 和 2x3 Boggle 上通过穷举搜索找到的得分最高的棋盘相匹配，在这种情况下，这是可行的。
  2. 它与在 3x4 Boggle 的单个棋盘类中通过穷举搜索找到的得分最高的棋盘相匹配。
  3. 它找到了我通过爬山法为 3x3、3x4 和 4x4 Boggle 找到的所有最佳棋盘。
  4. 树操作 preserve an invariant 在分数上，这表明它们是有效的。

下一步是什么？

我对 incremental optimizations 还有一些想法。但我已经在这个问题上 hacking 至少三个月了，这似乎是一个不错的停止点。我不确定 4x4 Boggle 是否会以这种方式“解决”，并且能够解决一个在我脑海中存在了 nearly 20 years 的问题，这令人非常满意。

我打算写一篇论文，更正式地解释我所做的事情，以及另一篇帖子，介绍我对整个经历的看法。

其他 word list 的得分最高的棋盘仍然需要证明。Hasbro 还销售 5x5 和 6x6 version 的 Boggle。这些问题比 4x4 Boggle 困难得多，可能需要等待下一代计算机和工具。我通过爬山法为 5x5 Boggle 找到的最佳棋盘是 sepesdsracietilmanesligdr。这次探索的结果表明，它也很可能是全局最优的。

请发表评论！这是写作的价值所在。