[Natural Intelligence](https://greydanus.github.io/2023/03/05/ncf-tutorial/</ >) Sam Greydanus 的博客 Home About me

使用梯度下降法寻找最小作用量路径

2023年3月5日 • Sam Greydanus, Tim Strang, 和 Isabella Caruso Play

这篇简单的文章旨在引起大家对物理学的一种观点的关注，这种观点在入门课程中并不常见：即物理学作为优化的观点。

这种方法从一个叫做作用量的量开始。 如果你最小化作用量，你可以获得一个最小作用量路径，它代表一个物理系统在空间和时间中采取的路径。 一般来说，物理学家使用分析工具来进行这种最小化。 在这篇文章中，我们将尝试一些不同的、有点疯狂的事情：使用梯度下降法最小化作用量。

阅读论文 在浏览器中运行 获取代码

在这篇文章中。 为了尽可能清晰和具体地传达这项技术，我们将把它应用到一个简单的玩具问题：重力场中的自由体。 但请记住，它同样适用于更大更复杂的系统，比如理想气体——我们将在论文和未来的博客文章中讨论这些系统。

现在，为了将我们的方法置于适当的背景下，我们将快速回顾解决此类问题的标准方法。

标准方法

分析方法。 在这里，你使用代数、微积分和其他数学工具来找到系统的运动方程的闭式解。 它给出系统状态作为时间的函数。 对于自由落体，运动方程是：

\[y(t)=-\frac{1}{2}gt^2+v_0t+y_0.\]

def falling_object_analytical(x0, x1, dt, g=1, steps=100):
  v0 = (x1 - x0) / dt
  t = np.linspace(0, steps, steps+1) * dt
  x = -.5*g*t**2 + v0*t + x0 # the equation of motion
  return t, x
x0, x1 = [0, 2]
dt = 0.19
t_ana, x_ana = falling_object_analytical(x0, x1, dt)

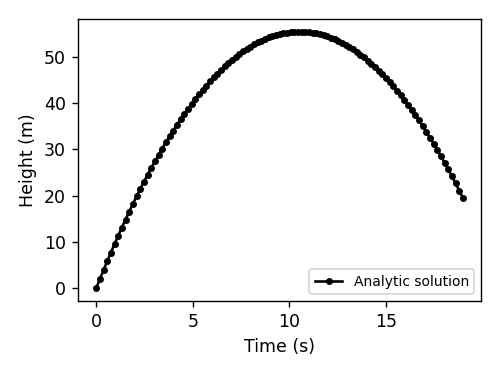
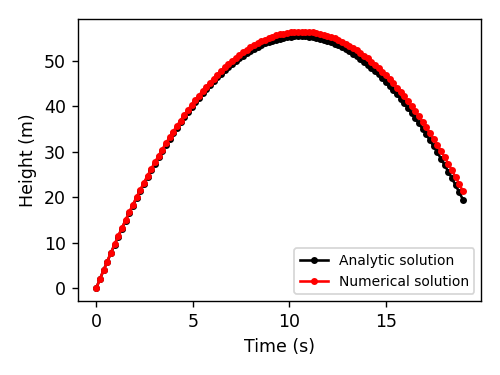
数值方法。 并非所有的物理问题都有解析解。 一些问题，例如双摆或三体问题，是确定性的但又是混沌的。 换句话说，它们的动力学是可预测的，但如果没有模拟所有中间状态，我们就无法知道它们在未来某个时刻的状态。 我们可以用数值积分来解决这些问题。 对于重力场中的物体，数值方法如下所示：

\[\frac{\partial y}{\partial t} = v(t) \quad \textrm{and} \quad \frac{\partial v}{\partial t} = -g\]

def falling_object_numerical(x0, x1, dt, g=1, steps=100):
  xs = [x0, x1]
  ts = [0, dt]
  v = (x1 - x0) / dt
  x = xs[-1]
  for i in range(steps-1):
    v += -g*dt
    x += v*dt
    xs.append(x)
    ts.append(ts[-1]+dt)
  return np.asarray(ts), np.asarray(xs)
t_num, x_num = falling_object_numerical(x0, x1, dt)

我们的方法：作用量最小化

拉格朗日方法。 我们刚才介绍的方法具有直观意义。 这就是为什么我们在入门物理课程中教授它们。 但是，还有一种完全不同的动力学观察方式，称为拉格朗日方法。 拉格朗日方法在描述现实方面做得更好，因为它可以为任何物理系统生成运动方程。1 拉格朗日量在物理学的四大分支中都占有重要地位：经典力学、电磁学、热力学和量子力学。 如果没有拉格朗日方法，物理学家将很难统一这些不同的领域。 但是有了标准模型拉格朗日量，他们就可以精确地做到这一点。

它是如何工作的。 拉格朗日方法首先考虑物理系统可能从初始状态 \(\bf{x}\)\((t_0)\)到最终状态 \(\bf{x}\)\((t_1)\)的所有路径。 然后，它提供了一个简单的规则来选择自然界实际采用的路径 \(\hat{\bf x}\)：作用量 \(S\)，定义在下面的方程中，必须在这个路径上具有一个平稳值。 这里 \(T\) 和 \(V\) 是系统在任何给定时间 \(t\) 在 \([t_0,t_1]\) 中的动能和势能函数。

\[\begin{aligned} S &:= \int_{t_0}^{t_1} L({\bf x}, ~ \dot{\bf x}, ~ t) ~ dt\\ &\quad \textrm{where}\quad L = T - V \\ \quad \hat{\bf x} &~~ \textrm{has property}~ \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{\hat{x}}(t)} \right) = \frac{\partial L}{\partial \hat{x}(t)} \\ &\textrm{for} \quad t \in [t_0,t_1] \end{aligned}\]

使用 Euler-Lagrange 方程寻找 \(\hat{\bf x}\) (人们通常的做法)。 当 \(S\) 是平稳的，我们可以证明 Euler-Lagrange 方程（上面等式的第三行）在区间 \([t_0,t_1]\) 上成立（Morin，2008）。 这个观察很有价值，因为它允许我们求解 \(\hat{\bf x}\)：首先，我们将 Euler-Lagrange 方程应用于拉格朗日量 \(L\)，并推导出一个偏微分方程组。2 然后，我们积分这些方程以获得 \(\hat{\bf x}\)。 重要的是，这种方法适用于跨越经典力学、电动力学、热力学和相对论的所有问题。 它为研究整个经典物理学提供了一个连贯的理论框架。

使用作用量最小化寻找 \(\hat{\bf x}\)（我们将要做的事情）。 找到 \(\hat{\bf x}\) 的一种更直接的方法始于这样的认识：平稳作用量的路径几乎总是也是最小作用量的路径（Morin 2008）。 因此，在不损失太多一般性的情况下，我们可以用下面等式的第三行中显示的简单最小化目标来交换 Euler-Lagrange 方程。 同时，如第一行所示，我们可以将 \(S\) 重新定义为 \(N\) 个均匀间隔的时间片的离散和：

\[\begin{aligned} S &:= \sum_{i=0}^{N} L({\bf x}, ~ \dot{\bf{x}}, ~ t_i) \Delta t \\ &\textrm{where} \quad \dot{\bf{x}} (t_i) := \frac{ {\bf x}(t_{i+1}) - {\bf x}(t_{i})}{\Delta t} \\ &\textrm{and} \quad \hat{\bf x} := \underset{\bf x}{\textrm{argmin}} ~ S(\bf x) \end{aligned}\]

还剩一个问题：在离散化 \( \hat{\bf{x}} \) 之后，我们不能再对其求导以获得 \( \dot{\bf{x}}(t_i) \) 的精确值。 相反，我们必须使用第二行中显示的有限差分近似。 当然，对于和中的最后一个 \( \dot{\bf{x}} \)，这种近似是不可能的，因为 \(\dot{\bf{x}}_{N+1}\) 不存在。 对于这个值，我们将假设，对于大的 \(N\)，区间 \( \Delta t \) 上的速度变化很小，因此让 \(\dot{\bf{x}}N = \dot{\bf{x}}{N-1}\)。 在做出这个最后的近似之后，我们现在可以数值计算梯度 \(\frac{\partial S}{\partial \bf{x}}\) 并用它来最小化 \(S\)。 这可以使用 PyTorch (Paszke et al, 2019) 或任何其他支持自动微分的包来完成。

一个简单的实现

让我们从坐标列表 x 开始，它包含系统在 t\(_1\) 和 t\(_2\) 之间的所有位置坐标。 我们可以用这些坐标来写出系统的拉格朗日量和作用量。

def lagrangian_freebody(x, xdot, m=1, g=1):
  T = .5*m*xdot**2
  V = m*g*x
  return T, V
 
def action(x, dt):
  xdot = (x[1:] - x[:-1]) / dt
  xdot = torch.cat([xdot, xdot[-1:]], axis=0)
  T, V = lagrangian_freebody(x, xdot)
  return T.sum()-V.sum()

现在让我们寻找一个平稳作用点。 从技术上讲，这可能是一个最小值或一个拐点。3 在这里，我们只是要寻找一个最小值：

def get_path_between(x, steps=1000, step_size=1e-1, dt=1, num_prints=15, num_stashes=80):
  t = np.linspace(0, len(x)-1, len(x)) * dt
  print_on = np.linspace(0,int(np.sqrt(steps)),num_prints).astype(np.int32)**2 # print more early on
  stash_on = np.linspace(0,int(np.sqrt(steps)),num_stashes).astype(np.int32)**2
  xs = []
  for i in range(steps):
    grad_x = torch.autograd.grad(action(x, dt), x)[0]
    grad_x[[0,-1]] *= 0 # fix first and last coordinates by zeroing their gradients
    x.data -= grad_x * step_size
    if i in print_on:
      print('step={:04d}, S={:.4e}'.format(i, action(x, dt).item()))
    if i in stash_on:
      xs.append(x.clone().data.numpy())
  return t, x, np.stack(xs)

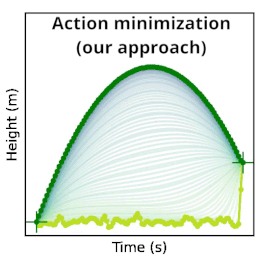
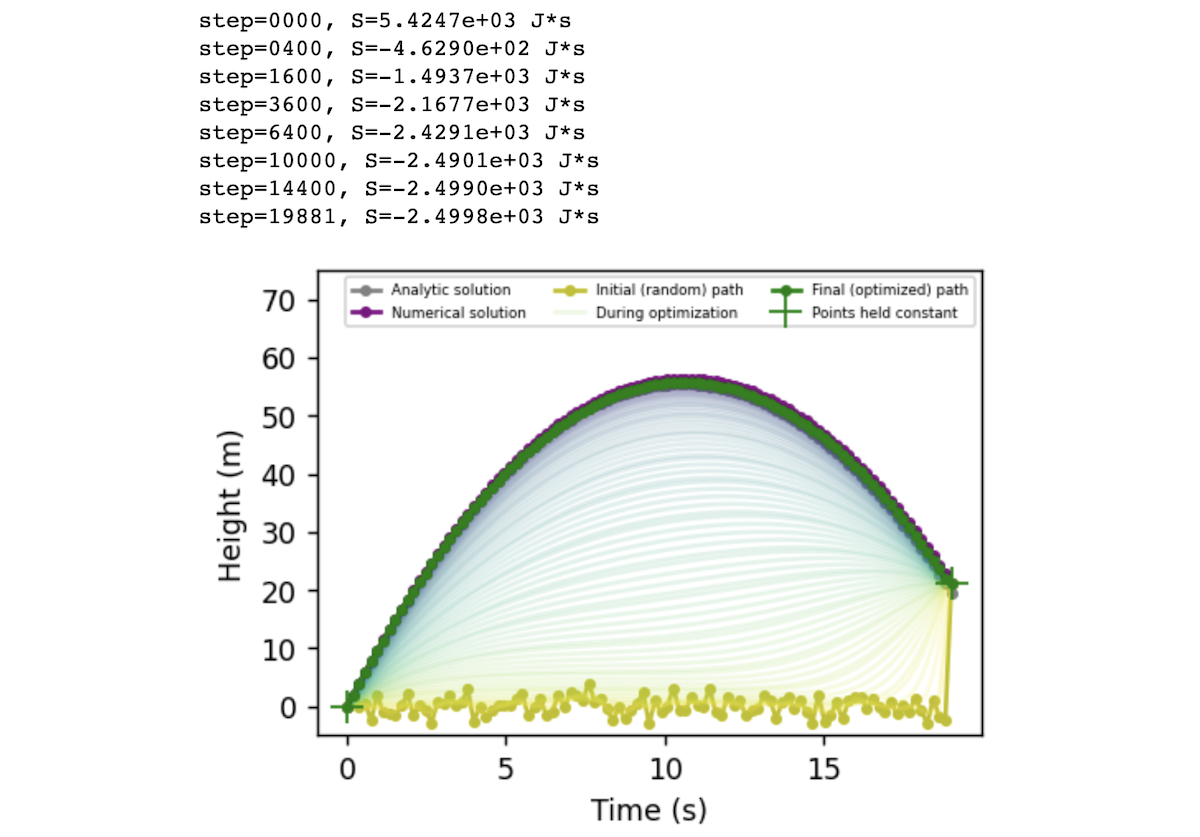
现在让我们把它们放在一起。 我们可以将我们自由落体的粒子的路径初始化为空间中的任何随机路径。 在下面的代码中，我们选择了一条路径，粒子在 x=0 附近随机弹跳，直到时间 t=19 秒，此时它跳到它的最终状态 x = x_num[-1] = 21.3 米。 这个路径有一个很高的作用量 S = 5425 J·s。 当我们运行优化时，这个值平稳下降，直到我们收敛到一个抛物线弧，作用量为 S = -2500 J·s。

dt = 0.19
x0 = 1.5*torch.randn(len(x_num), requires_grad=True) # a random path through space
x0[0].data *= 0.0 ; x0[-1].data *= 0.0 # set first and last points to zero
x0[-1].data += x_num[-1] # set last point to be the end height of the numerical solution

t, x, xs = get_path_between(x0.clone(), steps=20000, step_size=1e-2, dt=dt)

数值 (ODE) 解和我们的方法之间的直接比较

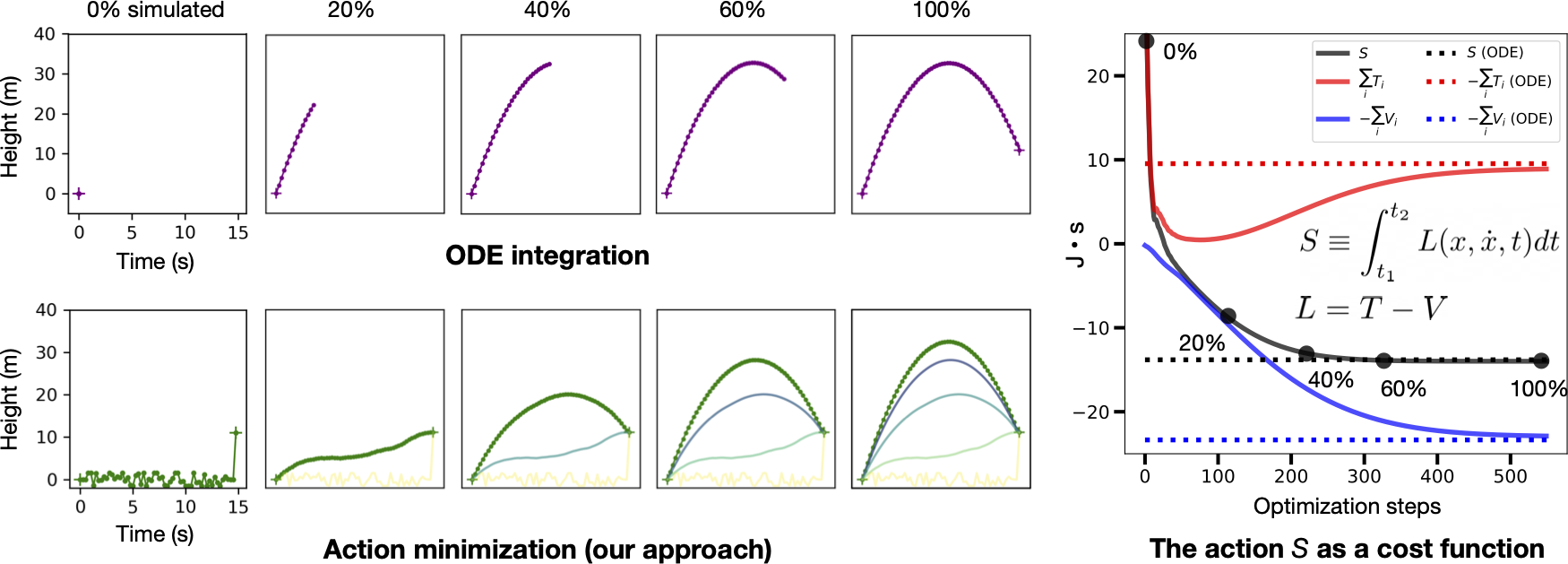
在下图中左侧，我们将 ODE 积分的常规方法与我们的作用量最小化方法进行了比较。 作为提醒，作用量是路径中每个点的动能 \(T\) 减去势能 \(V\) 的总和。 我们计算这个量相对于路径坐标的梯度，然后将初始路径（黄色）变形为最小作用量的路径（绿色）。 这个路径解析成一个抛物线，与通过 ODE 积分获得的路径相匹配。 在图的右侧，我们绘制了在优化过程中路径的作用量 \(S\)、动能 \(T\) 和势能 \(V\)。 所有三个量都渐近于 ODE 轨迹的相应值。

结束语

仿佛通过蛇缠绕的魔法，我们已经哄骗一条随机坐标的路径，使其发生蛇形过渡，变成一个结构化且有序的抛物线形状——自由体在恒定重力场影响下将采取的唯一轨迹的形状。 这是一个简单的例子，但我们已经详细研究了它，因为它说明了更广泛的“最小作用量原理”，该原理违背了自然人性的直觉，并塑造了我们物理宇宙的结构。

仅凭其名称的模糊性，即“作用量”，您可能会感觉到它不是一个被很好理解的现象。 在随后的文章中，我们将探讨它如何在更复杂的经典模拟中工作，然后，在量子力学领域中工作。 在那之后，我们将讨论它的历史：它是如何被发现的，以及它的发现者在发现它时是怎么想的。 最重要的是，我们将解决关于它到底意味着什么的挥之不去的推测。

脚注

  1. Tim 告诉我，有些弦理论不能被拉格朗日化。 因此，为了精确起见，我将把这个声明缩小到涵盖所有通过实验观察到的物理系统。 ↩
  2. 参见 Morin, 2008 以获得一个例子。 ↩
  3. 这就是为什么整个方法通常被称为最小作用量原理，这是一个用词不当的名称，我（和其他人）通过阅读 Feynman 讲义了解到这一点。 ↩

Sam Greydanus 的博客