使用 Inductive Graphs 生成迷宫 (2017)
使用 Inductive Graphs 生成迷宫
几年前——还在高中的时候——我花了一些时间编写程序来自动生成迷宫。这是一个有趣的练习,帮助我理解了递归:第一次用 Java 实现时,我无法让递归版本正常工作,所以最终使用了一个带有显式堆栈的 while 循环!
制作随机迷宫实际上是一个非常好的编程练习:它相对简单,能生成很酷的图片,并且很好地涵盖了图算法。对于函数式编程来说,它尤其有趣,因为它依赖于图 (graphs) 和 随机性 (randomness),这两者通常被认为在函数式风格中比较棘手。
因此,让我们看看如何使用 inductive graphs 在 Haskell 中实现一个迷宫生成器,用于我们的图遍历。这是我们的目标:
Inductive graphs 由 Haskell 的 “Functional Graph Library” fgl 提供。
与这篇文章相关的所有代码都在 GitHub 上,因此您可以将其加载到 GHCi 中并进行操作。如果您想稍后自己编写迷宫,这也是一个很好的起点。它全部采用 BSD3 许可,因此您可以随意使用它。
算法
我们可以通过从表示网格的图开始并生成随机 spanning tree 来生成一个 perfect 迷宫。Perfect 迷宫在任何两个点之间都只有一条路径——没有循环或封闭区域。图的 spanning tree 是连接图中每个节点的树。
我们可以使用多种算法来生成这样的树。让我们关注最简单的算法,它只是一个随机化的深度优先搜索 (DFS):
- 从一个填充了所有可能墙壁的网格开始
- 选择一个单元格作为起点
- 从当前单元格中,选择一个随机的、尚未访问过的相邻单元格
- 移动到所选的相邻单元格,拆掉它们之间的墙
- 如果没有未访问的相邻单元格,则回溯到之前的单元格并重复
- 否则,从新的单元格重复
我们的算法从一个网格开始,通过删除墙壁来生成一个迷宫。
Inductive Data Types
要编写我们的 DFS,我们需要某种方式来表示图。不幸的是,图在函数式语言中通常不太方便:像邻接矩阵或邻接表这样的标准表示是采用命令式思维设计的。虽然你肯定可以在 Haskell 中使用它们,但生成的代码会比较笨拙。
但是,Haskell 擅长处理哪些类型的结构呢?首先想到的是树和列表:我们可以通过模式匹配编写非常自然的代码。一个非常常见的模式是将列表视为头部元素和尾部,并在尾部上递归:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb1-1>)foo (x:xs) = bar x : foo xs
完全相同的模式对于树也很有用,我们在树的节点的子节点上进行递归:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb2-1>)foo (Node x children) = Node (bar x) (map foo children)
这种选择“第一个”元素,然后对结构的“其余部分”进行递归的模式非常强大。我喜欢将其视为将您的计算“分层”到数据结构的“形状”上。
我们可以非常自然地分解列表和树,因为这正是它们最初的构造方式:模式匹配只是正常使用构造函数的逆运算。甚至语法都一样!模式 (x:xs) 分解表达式 (x:xs) 的结果。并且由于我们只是遵循该类型固有的结构,因此总有一种方法可以拆分该类型。
这些类型的类型被称为 inductive data types,类似于数学归纳法。通常,它们有两个分支:一个基本情况和一个递归情况——就像归纳证明一样!考虑一个 List 类型:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb3-1>)data List a = Empty -- 基本情况
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb3-2>) | Cons a (List a) -- 归纳情况
非常简单明了。
不幸的是,图没有这种结构。图是由其节点和边的集合定义的——节点和边没有任何特定的顺序。我们无法通过添加节点和边以唯一的方式构建图,因为任何给定的图都可以通过多种不同的方式构建。因此,我们无法以唯一的方式分解图。我们无法对图进行模式匹配。我们的代码很笨拙。
Inductive Graphs
Inductive graphs 是我们可以查看的图,就好像它们是普通的 inductive data types 一样。我们可以拆分一个图并在其上递归,但这不像对列表那样是一种结构操作,更重要的是,它不是规范的:在任何时候,许多不同的图分解都可能是有意义的。
我们可以始终将图视为 empty,或者视为某个节点、其边以及图的其余部分。一个节点及其传入和传出边称为 context;这个想法是将图分解为一个 context 和其他所有内容,就像我们可以将列表分解为它的头元素和其他所有内容一样。
从概念上讲,这就像我们使用两个构造函数 Empty 和 :&(以中缀语法)定义了一个图:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb4-1>)data Graph = Empty
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb4-2>) | (Context [Edge] Node [Edge]) :& Graph
fgl 中的实际图视图有点不同,它支持节点和边标签,为了简单起见,我省略了这些标签。基本思想是相同的。
考虑一个小的示例图:
我们可以将此图分解为节点 1、其 context 和图的其余部分:

(Context [4,5,6] 1 []) :& graph 我们的图被分解为节点 1,其到 4、5 和 6 的边,以及图的其余部分。
但是,我们可以同样容易地将同一个示例图分解为节点 2 和其余部分:

(Context [5,6,7] 2 []) :& graph 另一种同样有效的方法来分解同一个图。
这意味着我们不能直接使用这个代数定义。相反,实际的图类型是 abstract 的,我们只是使用 contexts view 它,如上所述。与正常的模式匹配不同,view 一个 abstract type 不一定是构造它的逆运算。
我们通过使用一个匹配函数来实现这一点,该函数接受一个图并返回一个 context 分解。由于没有“自然”的第一个节点要返回,因此最简单的匹配函数 matchAny 返回一个 arbitrary (实现定义)分解:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb5-1>)matchAny :: Graph -> (Context, Graph)
在 fgl 中,Context 只是一个包含四个元素的元组:传入边、节点、节点标签和传出边。
使用 matchAny 最简单的方法是使用 case 表达式。这是图的 head 的道德等价物:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb6-1>)ghead :: Graph -> Graph.Node
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb6-2>)ghead graph | Graph.isEmpty graph = error "Empty graph!"
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb6-3>)ghead graph = case matchAny graph of
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb6-4>) ((_, node, _, _), graph) -> node
像这样使用 case 进行模式匹配有点笨拙。幸运的是,我们可以使用 ViewPatterns 获得更好的语法,它允许我们在模式中调用函数。这是一个更漂亮的 ghead 版本,它做的事情完全相同:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb7-1>)ghead :: Graph -> Node
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb7-2>)ghead graph | Graph.isEmpty graph = error "Empty graph!"
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb7-3>)ghead (matchAny -> ((_, node, _, _), graph)) = node
从现在开始,我的所有函数都将使用 ViewPatterns,因为它们会产生更好、更紧凑、更易读的代码。
由于 matchAny 返回的确切节点是实现定义的,因此通常不方便。我们可以使用 match 来克服这个问题,它匹配一个 specific 节点。
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb8-1>)match :: Node -> Graph -> (Maybe Context, Graph)
如果该节点不在图中,我们将得到 Nothing 作为我们的 context。此函数也可以用作 view pattern:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb9-1>)foo (match node -> (Just context, graph)) = ...
这使得对图进行 directed 遍历变得容易:我们可以“travel”到我们选择的节点。
一个真实的例子
fgl 中的所有函数实际上都是针对 Graph 类型类而不是具体的实现指定的。这种类型类机制很棒,因为它允许多个 inductive graphs 的实现。不幸的是,它也以有时难以追踪的方式破坏了类型推断,因此,为了简单起见,我们将只使用提供的实现:Gr。Gr n e 是一个图,其节点标记为 n,边标记为 e。
Map
递归列表函数的 “Hello, World!” 是 map,因此让我们首先看一下图的 map 版本。这个想法是将一个函数应用于图中的每个节点标签。
作为参考,这是列表 map:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb10-1>)map :: (a -> b) -> [a] -> [b]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb10-2>)map f [] = []
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb10-3>)map f (x:xs) = f x : map f xs
首先,我们有一个空列表的基本情况。然后我们分解列表,将函数应用于单个元素,并在其余部分递归。
图节点的 map 函数看起来非常相似:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb11-1>)mapNodes :: (n -> n') -> Gr n e -> Gr n' e
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb11-2>)mapNodes _ g | Graph.isEmpty g = Graph.empty
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb11-3>)mapNodes f (matchAny -> ((in', node, label, out), g)) =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb11-4>) (in', node, f label, out) & mapNodes f g
基本情况几乎完全相同。对于递归情况,我们使用 matchAny 将图分解为 some 节点和图的其余部分。对于该节点,我们实际上获得了一个 Context,其中包含传入边 (in')、传出边 (out)、节点本身 (node) 以及标签 (label)。我们只想将一个函数应用于标签,因此我们保持其余的 context 不变。最后,我们将图与 & 函数重新组合,& 函数是列表的 : 的图等价物。(尽管请注意,它 不是 构造函数,而只是一个函数!)
由于我们使用了 matchAny,因此我们映射图的确切顺序未定义!除此之外,代码感觉非常类似于针对正常的 Haskell 数据类型进行编程,并且很好地概括了 fgl。
DFS
我们的迷宫算法将是一个随机化的深度优先搜索。我们可以首先编写一个简单的、非随机的 DFS,然后从中获得我们的迷宫算法。这是我实现更困难算法的最喜欢的方式之一:从一些非常简单的东西开始并迭代。
基本的 DFS 实际上与 mapNodes 非常相似,除了我们将随着时间的推移构建访问过的节点列表,而不是构建一个新图。它也是一个 directed 遍历,不像 undirected map。
我们的第一个版本的 DFS 将获取一个图并从给定的节点开始遍历它,返回按顺序访问的节点列表。这是代码:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-1>)dfs :: Graph.Node -> Gr a b -> [Node]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-2>)dfs start graph = go [start] graph
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-3>) where go [] _ = []
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-4>) go _ g | Graph.isEmpty g = []
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-5>) go (n:ns) (match n -> (Just c, g)) =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-6>) n : go (Graph.neighbors' c ++ ns) g
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb12-7>) go (_:ns) = go ns g
核心逻辑在辅助函数 go 中。它有两个参数:一个列表,它是要访问的节点堆栈,以及图的其余部分。
go 的前两行是基本情况。如果我们在堆栈上没有任何节点或图中的节点已用完,我们就完成了。
递归情况更有趣。首先,我们从堆栈中获取要访问的节点 (n)。然后,我们使用它来 direct 我们与 match n 函数的匹配。如果这成功了,我们将 n 添加到我们的结果列表中,并将 n 的每个邻居推入堆栈。如果匹配失败,则意味着我们已经访问过该节点,因此我们忽略它并在堆栈的其余部分递归。
我们使用 neighbors' 函数查找节点的邻居,该函数获取 context 的邻居。在 fgl 中,以 ' 命名的函数通常作用于 contexts。
这里的重要思想是,我们不需要显式地跟踪我们访问过的节点——在访问一个节点之后,我们总是在不包含它的图的其余部分递归。这种行为对于一堆不同的图算法来说很常见,使得这成为一个非常有用的模式。
这是一个在之前示例图上运行 dfs 的快速演示。请注意,我们不需要跟踪我们访问过的节点,因为我们总是在只有未访问节点的图部分递归。
 堆栈:
堆栈:[7, 6]结果:[3] 堆栈:
堆栈:[4, 2, 6]结果:[3, 7] 堆栈:
堆栈:[1, 2, 6]结果:[3, 7, 4]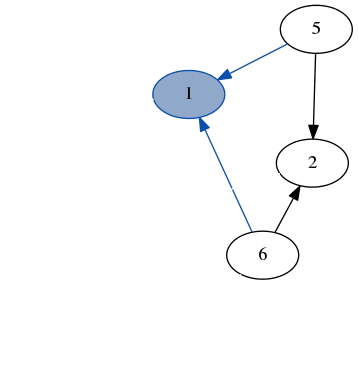 堆栈:
堆栈:[6, 5, 2, 6]结果:[3, 7, 4, 1] 堆栈:
堆栈:[2, 5, 2, 6]结果:[3, 7, 4, 1, 6]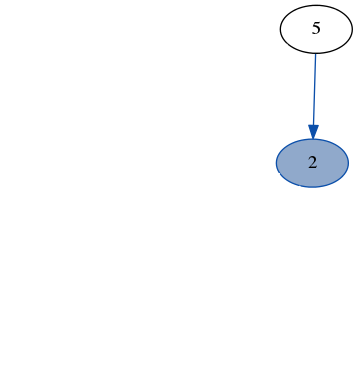 堆栈:
堆栈:[5, 5, 2, 6]结果:[3, 7, 4, 1, 6, 2] 堆栈:
堆栈:[5, 2, 6]结果:[3, 7, 4, 1, 6, 2, 5]
⇤▶⇥
通常——比如生成迷宫——我们不关心从哪个节点开始。这就是 ghead 的用武之地,因为它为我们选择了一个任意节点!唯一需要考虑的是 ghead 在空图上会失败。
EDFS
dfs 按照它们被访问的顺序给出我们节点。但是对于迷宫来说,我们真正关心的是我们遵循的 edges,而不是仅仅是节点。因此,让我们将我们的 dfs 修改为一个 edfs,它返回一个 edges 列表,而不是一个节点列表。在 fgl 中,一个 edge 只是一个由两个节点组成的元组:(Node, Node)。
从我们最初的 dfs 中进行的修改实际上非常轻微:我们保持一个 edges 堆栈,而不是一个节点堆栈。这需要修改我们的起始条件:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb13-1>)edfs start (match start -> (Just ctx, graph)) =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb13-2>) normalize $ go (neighborEdges' ctx) graph
由于我们在堆栈上存储了 edges,因此我们不能只是将起始节点直接放在上面。相反,我们只是匹配它并从堆栈上的 edges 开始。
我们需要额外调用 normalize,因为我们将 edges 视为无向 edges,并且我们需要确保定义一个 edge 的两个节点始终以相同的顺序出现。它只是遍历 edges,如果它们的顺序错误,则交换节点。
另一个改变是为了递归情况,我们在堆栈上推送 edges 而不是节点:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb14-1>)go ((p, n) : ns) (match n -> (Just c, g)) =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb14-2>) (p, n) : go (neighborEdges' c ++ ns) g
neighborEdges 只是一个辅助函数,它返回 context 中的所有传入和传出边。(在实际代码中,我称它为 lNeighbors,因为它实际上返回带标签的 edges。
Randomness
我们需要生成迷宫的最后一个改变是添加随机性。我们希望在将相邻 edges 列表放在堆栈上之前对其进行 shuffle。我们将使用 MonadRandom 类,它与许多其他 monads(如 IO)兼容。我写了一个天真的 O(n²) shuffle:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb15-1>)shuffle :: MonadRandom m => [a] -> m [a]
鉴于此,我们只需要修改 edfs 以使用它,这需要将所有内容提升到 monad 中。
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-1>)edfsR :: MonadRandom m => Graph.Node -> Gr n e -> m [(Node, Node)]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-2>)edfsR start (match start -> (Just ctx, graph)) =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-3>) liftM normalize $ go (lNeighbors' ctx) graph
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-4>) where go [] _ = return []
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-5>) go _ g | Graph.isEmpty g = return []
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-6>) go ((p, n):ns) (match n -> (Just c, g)) = do
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-7>) edges <- shuffle $ neighborEdges' c
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-8>) liftM ((p, n) :) $ go (edges ++ ns) g
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb16-9>) go (_:ns) g = go ns g
这些差异在很大程度上很简单并且是类型导向的:您必须添加一些对 return 和 liftM 的调用,但是您会得到一些不错的类型错误,这些错误告诉您 where 添加它们。唯一的另一个改变是使用带有 do-notation 的 shuffle,这很简单。
对于在函数式编程中应该很尴尬的事情,我认为代码实际上非常简洁且易于遵循!
由于我们使用了 MonadRandom 类,因此我们可以将 edfsR 与提供随机性功能的任何类型一起使用。这包括 IO,因此我们可以直接从 GHCi 使用它,这非常好。如果我们愿意,我们也可以通过提供种子以纯粹确定性的方式运行它。
Mazes
我们有一个随机 DFS,它给出了我们一个 edges 列表——迷宫生成算法的核心。但是,很难从一组 edges 到绘制迷宫。拼图的最后一部分是标记 edges 的方式便于绘制,并生成初始网格的图。
这是我们首次使用 edge labels 的地方。每个 edge 代表一堵墙,我们需要足够的信息来绘制它。我们需要知道墙的 location 及其 orientation(水平或垂直)。为了简单起见,我们将根据单元格的位置来定位墙,该单元格位于墙下方或右侧,具体取决于其方向。以下是相关类型:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb17-1>)data Orientation = Horizontal | Vertical deriving (Show, Eq)
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb17-2>)
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb17-3>)data Wall = Wall (Int, Int) Orientation deriving (Show, Eq)
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb17-4>)
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb17-5>)type Grid = Gr () Wall -- () 表示不需要节点 labels
接下来,我们需要构建起始图:一个包含每堵墙的迷宫。我们可以使用 mkGraph 函数组装它,该函数采用节点列表和 edges 列表。我们希望用其位置和方向标记每个 edge。可能有一种更好的方法可以做到这一切,但是现在我利用了 Node 只是 Int 的别名这一事实:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-1>)grid :: Int -> Int -> Grid
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-2>)grid width height = Graph.mkGraph nodes edges
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-3>) where nodes = [(node, ()) | node <- [0..width * height - 1]]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-4>) edges = [(n, n', wall n Vertical) |
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-5>) (n, _) <- nodes,
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-6>) (n, _) <- nodes,
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-7>) n - n' == 1 && n `mod` width /= 0 ]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-8>) ++ [(n, n', wall n Horizontal) |
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-9>) (n,_) <- nodes,
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-10>) (n',_) <- nodes,
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-11>) n - n' == width ]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb18-12>) wall n = let (y, x) = n `divMod` width in Wall (x, y)
 一个 3 × 3 网格。edges 标有 (x, y) 位置和
一个 3 × 3 网格。edges 标有 (x, y) 位置和 Horizontal (—) 或 Vertical (|)。
在起始迷宫上运行 edfsR 将给出我们 knocked down 的墙壁列表——它们是我们不想绘制的墙壁。我们可以使用 Data.List 中的列表差异运算符 \\\\ 轻松地从这个列表到绘制的墙壁的补充列表:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb19-1>)maze :: MonadRandom m => Int -> Int -> m [Graph.Edge]
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb19-2>)maze width height =
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb19-3>) liftM (Graph.edges graph \\) $ edfsR (ghead graph) graph
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb19-4>) where graph = grid width height
由于网格始终具有节点,因此我们可以安全地使用 ghead。
这会生成一个从图中绘制的 edges 列表。要实际绘制它们,我们将首先在网格中查找它们的 labels,然后使用位置和方向来确定墙壁的绝对位置。(我的实际实现会跟踪 edge labels,因为它会执行 DFS。)
所有绘图代码都在 Draw.hs 中,并使用 cairo 进行实际绘图。Cairo 是一个 C 库,它提供的东西与 HTML Canvas 非常相似,但适用于 GtK;它也可以输出图像。如果您只是想玩迷宫,可以使用以下命令将其绘制到 png:
[](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<#cb20-1>)genPng defaults "my-maze.png" 40 40
更有趣
我们现在有一个使用 inductive graphs 和 randomness 的基本迷宫生成系统。如果您想稍微玩一下代码,有两种有趣的方式可以扩展此代码:从其他形状生成迷宫并使用不同的图算法。
其他形状
我们的系统始终假设迷宫是从单元格网格生成的。但是,实际的图代码根本不在乎这一点!特定于网格的部分只是起始图(即 grid 40 40)和绘图代码。
一个有趣的挑战是看看其他类型的图上的迷宫是什么样的。尝试编写一个基于平铺六边形、极坐标矩形甚至任意(可能是随机的?)平面平铺的迷宫生成器。或者尝试在 3D 中生成迷宫!
其他算法
除了修改图之外,我们还可以修改我们的遍历。尝试使用 DFS 代码:例如,您可以替换为有偏的 shuffle 并获得其他形状的迷宫。如果您使 shuffle 更倾向于选择水平墙而不是垂直墙,您将获得一个具有更长垂直通道和更短水平通道的迷宫。您还可以如何改变 DFS?
随机 DFS 是生成迷宫的一个不错的算法,因为它很简单并且可以生成美观的迷宫。但它不是唯一的可能算法。您可以采用一些其他算法来生成 spanning trees 并将它们随机化。
一个特别的技巧是采用生成 minimum spanning trees 的算法,并将其应用于具有随机 edge 权重的图。两种常见的 minimum spanning tree 算法是 Prim’s algorithm 和 Kruskal’s algorithm——实现这些算法是一个很好的 Haskell 练习,并且会产生外观略有不同的迷宫。查看 Wikipedia 上的 [Minimum Spanning Tree Algorithms](https://jelv.is/blog/Generating-Mazes-with-Inductive-Graphs/<http:/en.wikipedia.org/




