自动稀疏微分(Automatic Sparse Differentiation)图解指南
自动稀疏微分(Automatic Sparse Differentiation)图解指南
在许多机器学习应用中,Hessian 矩阵和 Jacobian 矩阵呈现出稀疏性,这一特性可以被利用来极大地加速它们的计算。虽然自动微分(automatic differentiation)在机器学习中应用广泛,但自动稀疏微分(automatic sparse differentiation,ASD)仍然鲜为人知。本文将介绍 ASD,解释其关键组成部分以及它们在计算稀疏 Jacobian 矩阵和 Hessian 矩阵中的作用。最后,我们将通过一个实际演示来展示 ASD 的性能优势。
作者
机构
BIFOLD – Berlin Institute for the Foundations of Learning and Data, Machine Learning Group, Technical University of Berlin, Berlin, Germany
LVMT, ENPC, Institut Polytechnique de Paris, Univ Gustave Eiffel, Marne-la-Vallée, France
Argonne National Laboratory, Lemont, USA
发布时间
April 28, 2025
目录
一阶优化在机器学习(ML)中无处不在,但二阶优化却不那么常见。 直观的原因是高维向量(梯度)很便宜,而高维矩阵(Hessian 矩阵)很昂贵。 幸运的是,在许多 ML 在科学或工程方面的应用中,Hessian 矩阵和 Jacobian 矩阵表现出稀疏性:它们的大部分系数已知为零。 利用这种稀疏性可以极大地加速 Hessian 矩阵和 Jacobian 矩阵的自动微分(AD),同时减少其内存需求。 然而,虽然传统的 AD 在许多高级编程语言(如 Python 和 Julia)中可用,但自动稀疏微分(ASD)并未得到广泛使用。 原因之一是,底层的理论是在 AD 社区中开发的,而不是在 ML 研究生态系统之外。
通过这篇博文,我们旨在阐明 ASD 的内部工作原理,通过介绍后一个领域中已建立的技术来弥合 ML 社区和 AD 社区之间的差距。 我们首先简要介绍传统的 AD,涵盖前向模式和反向模式下 Jacobian 矩阵的计算。 然后,我们深入研究 ASD 的两个主要组成部分:稀疏模式检测和矩阵着色。 在描述了稀疏 Jacobian 矩阵的计算后,我们继续介绍稀疏 Hessian 矩阵。 在讨论了机器学习中的应用之后,我们以 ASD 的实际演示作为结尾,提供性能基准,并指导何时在 AD 上使用 ASD。
自动微分
让我们从介绍传统 AD 的基础知识开始。读者可以在 Blondel 和 Roulet 的最新著作以及 Griewank 和 Walther 的著作中找到更多详细信息。
AD 利用了数学函数(如深度神经网络)的组合结构。 为了简单起见,我们将主要研究由两个可微函数 g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{p} 和 h: \mathbb{R}^{p} \rightarrow \mathbb{R}^{m} 组成的可微函数 f,使得 f = h \circ g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}。 从这个玩具示例中获得的见解应该直接转化为更深入的组合函数 f = g^{(L)} \circ g^{(L-1)} \circ \cdots \circ g^{(1)},甚至是具有更复杂分支的计算图。
链式法则
对于函数 f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m} 和线性化点 \mathbf{x} \in \mathbb{R}^{n},Jacobian 矩阵 J_f(\mathbf{x}) 是 m \times n 的一阶偏导数矩阵,其 (i,j)-th 项为
(Jf(x))i,j=∂fi∂xj(x)∈R.
对于组合函数
f=h∘g,
多元链式法则告诉我们,通过乘以 h 和 g 的 Jacobian 矩阵,我们可以获得 f 的 Jacobian 矩阵:
Jf(x)=Jh(g(x))⋅Jg(x).
图 1 说明了 n=5、m=4 和 p=3 的情况。 我们将在后续的说明中继续使用这些维度,即使 ASD 的真正好处只有在维度增长时才会显现。
图 1:f = h \circ g 的多元链式法则可视化。
AD 是无矩阵的
我们已经看到了链式法则如何将函数的组合结构转化为其 Jacobian 矩阵的乘积结构。 然而,在实践中存在一个问题:计算中间 Jacobian 矩阵效率低下且通常难以处理,特别是使用密集矩阵格式。 密集矩阵格式的示例包括 NumPy 的 ndarray、PyTorch 的 Tensor、JAX 的 Array 和 Julia 的 Matrix。
作为一个激励性的例子,让我们看一下一个小的卷积层。 我们考虑一个大小为 5 \times 5 的卷积滤波器,一个输入通道和一个输出通道。 大小为 28 \times 28 \times 1 的输入产生 576 维的输出,因此产生一个 576 \times 784 的 Jacobian 矩阵,其结构如图 2 所示。所有白色系数都是结构零。
如果我们将每个卷积层的 Jacobian 矩阵表示为密集矩阵,我们就会浪费时间计算大多为零的系数,并且浪费内存来存储这些零系数。
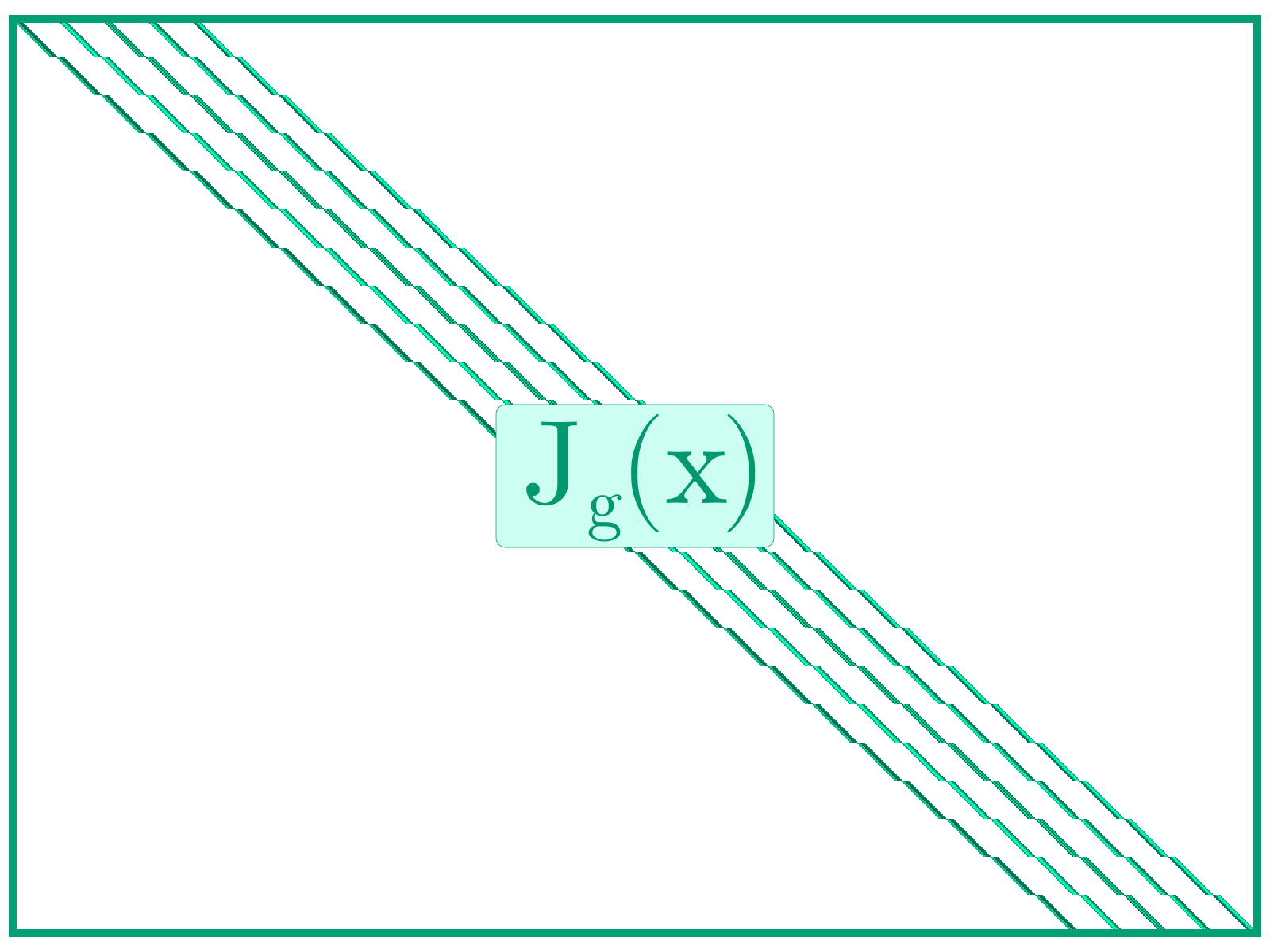
图 2:一个小的卷积层的 Jacobian 矩阵的结构。
在现代神经网络架构中,神经网络可以包含超过 1 万亿个参数,计算中间 Jacobian 矩阵不仅效率低下:它还会超出可用内存。
AD 通过使用Jacobian 算子来规避此限制,这些算子的作用与 Jacobian 矩阵完全相同,但无需在内存中显式存储每个系数。 Jacobian 算子 Df: \mathbf{x} \longmapsto Df(\mathbf{x}) 是一个线性映射,它提供了函数 f 在给定点 \mathbf{x} 附近的最佳线性近似。 Jacobian 矩阵是标准基中 Jacobian 算子的表示。
我们现在可以将链式法则重新表述为算子的组合,而不是矩阵的乘积:
Df(x)=D(h∘g)(x)=Dh(g(x))∘Dg(x).
请注意,此公式中链式法则的所有项都是 Jacobian 算子。 我们玩具示例的一个新可视化可以在图 3b 中找到。 我们的图示通过分别使用实线和虚线来区分矩阵和算子。
图 3a:使用 Jacobian 矩阵(实线轮廓)的链式法则。
图 3b:使用无矩阵 Jacobian 算子(虚线轮廓)的链式法则。
我们在 Jacobian 算子中可视化“矩阵条目”以建立直觉。 即使后续图示有时会将数字放到这些条目上,最好还是将 Jacobian 算子视为黑盒。
前向模式 AD
现在我们已经将函数 f 的组合结构转化为 Jacobian 算子的组合结构,我们可以通过一次一个子函数地通过它们传播向量来评估它们。
图 4 说明了从右侧传播向量 \mathbf{v}_1 \in \mathbb{R}^n。 由于我们按照原始函数评估的顺序(先 g 后 h)进行传播,因此这称为前向模式 AD。
图 4:在前向模式下评估 Jacobian 算子。
在第一步中,我们评估 Dg(\mathbf{x})(\mathbf{v}_1)。 由于此操作按定义对应于
v2=Dg(x)(v1)=Jg(x)⋅v1∈Rp,
它通常被称为 Jacobian-向量积(JVP)或 pushforward。
尽管由于它在 ML 社区中的流行,我们坚持使用术语“JVP”,但我们想强调的是,它具有误导性:JVP 不会实现和乘以 Jacobian 矩阵。 相反,它评估无矩阵 Jacobian 算子。
然后,将生成的向量 \mathbf{v}_2 用于计算后续的 JVP
v3=Dh(g(x))(v2)=Jh(g(x))⋅v2∈Rm,
根据链式法则,这等效于
v3=Df(x)(v1)=Jf(x)⋅v1,
我们组合函数 f 的 JVP。
f 的一个 JVP 的计算成本大约与 f 的一次评估的成本相同。 请注意,我们没有在任何时候计算中间 Jacobian 矩阵——我们只是通过 Jacobian 算子传播向量。
反向模式 AD
我们还可以从左侧通过 Jacobian 算子传播向量,从而产生反向模式 AD,如图 5 所示。
图 5:在反向模式下评估 Jacobian 算子。
这通常称为 向量-Jacobian 积(VJP)或 pullback。 就像前向模式一样,f 的一个 VJP 的成本大约与 f 的一次评估的成本相同。 然而,内存占用更大,因为 f 计算的中间结果必须保存在内存中(例如,层之间的隐藏激活)。 反向模式也是无矩阵的:在任何时候都不会计算中间 Jacobian 矩阵。
就像前向模式中的术语“JVP”一样,术语“VJP”也具有误导性。 VJP 不会实现和乘以 Jacobian 矩阵。 相反,它评估无矩阵 Jacobian 算子。
从 Jacobian 算子回到 Jacobian 矩阵
在一个计算成本很高的过程中,我们称之为物化,我们可以将 Jacobian 算子的组合转化为一个密集的 Jacobian 矩阵。 与直觉相反,此过程不会物化任何中间 Jacobian 矩阵。
图 6 演示了如何在前向模式下逐列物化 Jacobian 矩阵。 在 i-th 标准基向量上评估 Jacobian 算子 Df(\mathbf{x}) 可以物化 Jacobian 矩阵 J_{f}(\mathbf{x}) 的 i-th 列:
Df(x)(ei)=(Jf(x))i,:
因此,要恢复完整的 m \times n Jacobian 矩阵,需要对输入空间的每个 n 个标准基向量执行一个 JVP。 再次,我们通过分别使用虚线和实线来区分 Jacobian 算子和物化的 Jacobian 矩阵。 虽然为了说明目的,我们将数字放入 Jacobian 算子中,但最好将它们视为黑盒函数:
图 6:前向模式 AD 逐列物化 Jacobian 矩阵。
如图 7 所示,我们也可以在反向模式下逐行物化 Jacobian 矩阵。 与图 6 中的前向模式不同,这需要对输出空间的每个 m 个标准基向量执行一个 VJP。
图 7:反向模式 AD 逐行物化 Jacobian 矩阵。
由于每个 JVP 和 VJP 的成本大约与函数 f 自身的评估成本一样高,因此这些物化过程的计算成本很高。
由于神经网络通常使用标量损失函数进行训练,因此反向模式 AD 只需要评估单个 VJP 即可物化梯度,这相当便宜(请参阅 Baur 和 Strassen)。 这使得反向模式 AD 成为机器学习者的首选方法,他们通常使用术语反向传播。
自动稀疏微分
稀疏矩阵
稀疏矩阵是指大多数元素为零的矩阵。 如图 8 所示,如果 Jacobian 算子物化为稀疏矩阵,我们将它们称为“稀疏算子”。
图 8:一个稀疏 Jacobian 矩阵及其对应的稀疏 Jacobian 算子。
当函数有许多输入和许多输出时,给定的输出并不总是依赖于每个输入。 这使相应的 Jacobian 矩阵具有稀疏模式,其中零系数表示缺少(一阶)依赖关系。 前面的卷积层的情况就是一个简单的例子。 一个更简单的例子是按元素应用激活函数,对于该函数,Jacobian 矩阵是单位矩阵。
利用稀疏性
现在,我们假设 Jacobian 矩阵的稀疏模式始终相同,而与输入无关,并且我们事先知道它。 如果 Jacobian 矩阵的两列或两行对于每个索引,最多只有一个具有非零系数,我们就说它们在结构上是正交的。 换句话说,这些列的稀疏模式是非重叠的向量,无论它们的实际值如何,它们的点积始终为零。
ASD 的核心思想是我们可以使用单个 JVP(或 VJP)物化多个结构上正交的列(或行)。 这个技巧最早是由 Curtis、Powell 和 Reid 在 1974 年提出的。 由于 Jacobian 算子是线性映射,因此是可加的,因此对于一组基向量,它始终成立
Df(x)(ei+…+ej)=Df(x)(ei)⏟(Jf(x))i,:+…+Df(x)(ej)⏟(Jf(x))j,:.
右侧和中的分量各自对应于 Jacobian 矩阵的一列。 如果已知这些列在结构上是正交的,则可以将总和唯一地分解为其分量,该过程称为解压缩。 因此,单个 JVP 足以一次检索多个列的非零系数。
此使用 JVP 的特定示例对应于前向模式 ASD,如图 9 所示,其中所有结构上正交的列都已着色为匹配的色调。 通过使用向量 \mathbf{e}_1 + \mathbf{e}_2 + \mathbf{e}_5 计算单个 JVP,我们可以获得 Jacobian 矩阵的第一列、第二列和第五列的总和。
图 9:在前向模式下物化 Jacobian 矩阵的结构上正交的列。
使用向量 \mathbf{e}_3 + \mathbf{e}_4 的第二个 JVP 为我们提供了其余列的总和。 然后,我们将生成的向量中的值分配回 Jacobian 矩阵的相应条目。 此最终的解压缩步骤如图 10 所示。
图 10:使用前向模式 ASD 物化 Jacobian 矩阵:(a) 正交列的压缩评估 (b) 解压缩到 Jacobian 矩阵
相同的想法也可以应用于反向模式 AD,如图 11 所示。 我们不依赖于正交列,而是依赖于正交行。 然后,我们可以在单个 VJP 中物化多个行。
图 11:使用反向模式 ASD 物化 Jacobian 矩阵:(a) 正交行的压缩评估 (b) 解压缩到 Jacobian 矩阵
模式检测和着色
不幸的是,我们最初的假设存在一个主要缺陷。 由于 AD 仅为我们提供 Jacobian 算子的组合(即黑盒函数),因此相应 Jacobian 矩阵的结构是完全未知的。 换句话说,在不首先物化 Jacobian 矩阵的情况下,我们无法判断哪些行和列构成结构上正交的组。 但是,如果我们通过传统的 AD 物化此矩阵,则不再需要 ASD。
图 12 (a) 显示了此问题的解决方案:为了找到结构上正交的列(或行),我们不需要物化完整的 Jacobian 矩阵。 相反,足以检测矩阵的稀疏模式。 此二进制值模式包含足够的信息来推断结构正交性。 从那里,我们使用着色算法将正交列(或行)分组在一起。 这样的着色可以在图 12 (b) 中可视化,其中黄色列将一起评估(第一个 JVP),浅蓝色列将一起评估(第二个 JVP),总共 2 个 JVP 而不是 5 个 JVP。
图 12:ASD 的前两个步骤:(a) 稀疏模式检测,(b) 稀疏模式着色。
总而言之,ASD 包含四个步骤:
- 模式检测
- 着色
- 压缩 AD
- 解压缩
Gebremedhin、Manne 和 Pothen 在他们的重要调查中或在 Griewank 和 Walther 的书的第 8 章中详细描述了此基于压缩的流水线。 同一本书的第 7 章介绍了另一种直接流水线。
我们现在更详细地讨论前两个步骤。 这些步骤可能比对函数 f 的单个调用慢得多,但它们通常比使用 AD 完全计算 Jacobian 矩阵快得多。 这使得稀疏过程即使对于中等大小的矩阵也是值得的。 此外,如果我们需要多次计算 Jacobian 矩阵(对于不同的输入)并且能够重用稀疏模式和着色结果,则可以在多个后续评估中摊销此前奏的成本。
模式检测
镜像 AD 系统的多样性,也存在许多可能的稀疏模式检测方法,每种方法都有其自身的优势和权衡。 Dixon 在 1990 年代的工作是关于此主题的许多论文中的第一篇,其中大多数论文可以分为运算符重载或源转换技术。 还有一些方法可以通过使用 AD 探测 Jacobian 矩阵系数来检测稀疏模式,但我们在此不作赘述。
我们展示的方法对应于前向模式 AD 系统的二进制版本,在精神上与 和 类似,其中通过将矩阵行表示为索引集来提高性能。
索引集
我们使用稀疏模式检测的目标是快速计算 Jacobian 矩阵的二进制模式。 实现比传统 AD 更好的性能的一种方法是将行稀疏模式编码为索引集。 Jacobian 矩阵的 i-th 行由下式给出
(Jf(x))i,:=[∂fi∂xj(x)]1≤j≤n=[∂fi∂x1(x)…∂fi∂xn(x)].
但是,由于我们只对二进制模式感兴趣
[∂fi∂xj(x)≠0]1≤j≤n,
我们可以改为通过非零值的相应索引集来表示 Jacobian 矩阵的 i-th 行的稀疏模式
{j|∂fi∂xj(x)≠0}.
这些等效的稀疏模式表示如图 13 所示。 每个行索引集告诉我们哪些输入影响给定的输出,这是一阶的。 例如,输出 i=2 受输入 j=4 和 j=5 的影响。
图 13:稀疏模式表示:(a) 原始矩阵,(b) 二进制模式,(c) 行索引集。
高效传播
图 14 显示了我们想要避免的传统前向模式传递:通过 Jacobian 算子传播完整的单位矩阵不仅会物化 f 的 Jacobian 矩阵,还会物化所有中间 Jacobian 矩阵。 如前所述,由于其效率低下和高内存需求,这不是一个可行的选择。
图 14:在前向模式下传播单位矩阵以获得 Jacobian 矩阵。
相反,我们使用与单位矩阵对应的索引集初始化输入向量。 对此向量的另一种看法是,它对应于输入的 Jacobian 矩阵的索引集表示,因为 \frac{\partial x_i}{\partial x_j} \neq 0 仅适用于 i=j。
我们的目标是传播此索引集,以便我们获得与 Jacobian 稀疏模式对应的索引集的输出向量。 此想法如图 15 所示。
图 15:通过 Jacobian 算子传播索引集以获得稀疏模式。
抽象解释
我们不想深入研究实现细节,而是想提供有关此典型前向模式稀疏检测系统的第二个关键成分的一些直觉:抽象解释。
我们将在第二个玩具示例(函数)上演示这一点
f(x)=[x1x2+sgn(x3)sgn(x3)x42].
相应的计算图如图 16 所示,其中圆形节点对应于基本函数,在本例中为加法、乘法、除法和符号函数。 标量输入 x_i 和输出 y_j 显示在矩形节点中。 不是为给定输入 \mathbf{x} 评估原始计算图,而是使用其相应的输入索引集播种所有输入。 图 16 在计算图的边缘上注释了这些索引集。
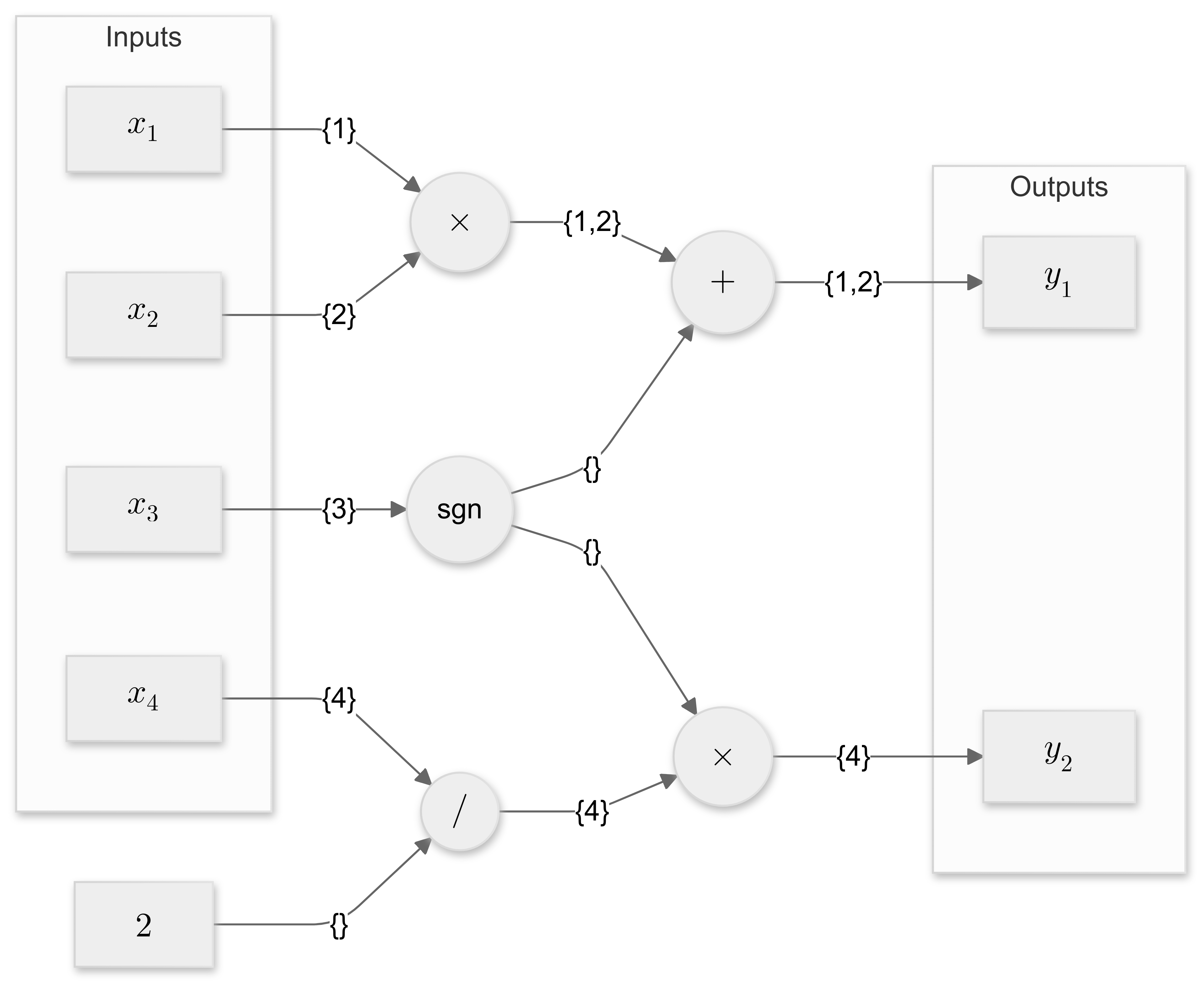
图 16:函数 f(\mathbf{x}) = [x_1 x_2 + \text{sgn}(x_3),, \text{sgn}(x_3) \frac{x_4}{2} ] 的计算图,并带有相应的索引集。
抽象解释意味着我们赋予计算图不同的含义。 每个基本函数不是计算其输出值,而是必须累积其输入的索引集,然后将这些索引集传播到输出,但前提是相应的导数在输入域中的任何位置都不是零。
由于加法、乘法和除法在全局上具有相对于其两个输入的非零导数,因此会累积并传播其输入的索引集。 符号函数对于任何输入值都有零导数。 因此,它不会传播其输入的索引集,而是返回一个空集。
图 16 显示了输出 1 和 2 的结果输出索引集 \{1, 2\} 和 \{4\}。 这些与分析 Jacobian 矩阵匹配
Jf(x)=[x2x100000sgn(x3)2].
局部和全局模式
上面显示的抽象解释类型对应于_全局稀疏检测_,计算索引集
{j|∂fi∂xj(x)≠0forsomex∈Rn}
在整个输入域中有效。 可以实现另一种抽象解释类型,其中原始_原始计算_与索引集一起传播,计算
{j|∂fi∂xj(x)≠0}
对于特定的输入 \mathbf{x}。 这些_局部稀疏模式_是全局稀疏模式的严格子集,因此可以减少颜色。 但是,更改输入时需要重新计算它们。
着色
一旦我们检测到稀疏模式,我们的下一个目标就是决定如何对 Jacobian 矩阵的列(或行)进行分组。 每个组中的列(或行)将使用单个 JVP(或 VJP)同时评估,其中基向量的线性组合称为种子。 如果组的成员在结构上是正交的,那么这将提供检索矩阵的每个非零系数的所有必要信息。
图公式
幸运的是,此分组问题可以重新表述为图着色,这已得到很好的研究。 让我们构建一个图 \mathcal{G} = (\mathcal{V}, \mathcal{E}),其中顶点集为 \mathcal{V},边集为 \mathcal{E},这样每列都是图的顶点,并且当且仅当它们各自的列共享非零索引时,两个顶点才连接。 换句话说,顶点 j_1 和 j_2 之间的边意味着列 j_1 和 j_2 在结构上不是正交的。 请注意,中总结了更有效的图表示形式。
我们想要为每个顶点 j 分配一种颜色 c(j),这样任何两个相邻的顶点 (j_1, j_2) \in \mathcal{E} 都具有不同的颜色 c(j_1) \neq c(j_2)。 此约束确保同一颜色组中的列确实在结构上是正交的。 如果我们可以找到使用尽可能少的不同颜色的着色,它将最大限度地减少组的数量,从而最大限度地降低 AD 步骤的计算成本。
图 17 显示了使用两种颜色的最佳着色,而图 18 使用次优的第三种颜色,需要额外的 JVP 来物化 Jacobian 矩阵,从而增加了 ASD 的计算成本。 图 19 显示了一种不可行的着色:图上的顶点 2 和 4 是相邻的,但共享一种颜色。 这会导致列重叠。
图 17:最佳图着色。
图 18:次优图着色(顶点 1 可以用黄色着色)。
图 19:不可行的图着色(图上的顶点 2 和 4 相邻,但共享一种颜色)。
如果我们执行列着色,则需要前向模式 AD,而对于行着色,则需要反向模式 AD。
贪婪算法
不幸的是,图着色问题是 NP 难题:目前没有办法在多项式时间内为每个实例解决它。 仅对于特定模式(例如条带矩阵)才知道最佳解决方案。 然而,存在有效的启发式方法,可以在合理的时间内生成足够好的解决方案。 最广泛使用的启发式方法是贪婪算法,它会逐个处理顶点。 此算法为每个顶点分配尚未在其邻居中出现的最小颜色,并且它永远不会回溯。 一个关键的超参数是排序的选择,为此提出了各种标准。
双着色
一种称为双着色的更高级着色技术允许组合前向模式和反向模式,因为 Jacobian 矩阵的恢复利用了列(JVP)和行(VJP)。
图 20 显示了玩具示例上的双着色,其中没有一对列或行在结构上是正交的。 即使使用 ASD,物化 Jacobian 矩阵也需要在前向模式下进行 5 个 JVP,或者在反向模式下进行 4 个 VJP。 但是,如果我们同时使用这两种模式,我们可以通过仅计算 1 个 JVP 和 1 个 VJP 来物化完整的 Jacobian 矩阵。
图 20:在具有密集行和密集列的玩具示例上进行双着色。
二阶
虽然一阶自动微分 AD 侧重于计算梯度或 Jacobian 矩阵,但二阶 AD 将相同的思想扩展到 Hessian 矩阵
∇2f(x)=(∂2f(x)∂xi∂xj)i,j.
Hessian 矩阵包含标量函数的二阶偏导数,本质上捕获函数在某个点的曲率。 这在优化中尤其相关,其中 Hessi





















