Liverpool FC 在周末的胜利为他们锁定了第二个Premier League冠军，但同时也产生了一些奇妙的事情——在联赛的记录簿中产生了一个奇怪的数字序列。

英国足球界刚刚发生了一件引人注目的大事。Liverpool FC 第二次 荣获Premier League冠军。加上他们在Premier League时代之前的 18 个冠军头衔，这意味着他们现在追平了Manchester United 20 次获得英格兰冠军的记录。虽然俱乐部的球迷无疑会庆祝这一胜利时刻，但他们成就的另一个惊人之处引起了数学家的注意。

利物浦的冠军胜利完成了一个非凡的数字序列的开端，这个序列酝酿了 33 年。当我们把利物浦与自 1992 年首次成立以来赢得Premier League的其他俱乐部放在一起排名时，这个序列就会显现出来，按照他们赢得的冠军数量，从最少到最多进行排列。如下表所示，Premier League冠军的数量如下：1, 1, 2, 3, 5, 8, 13。

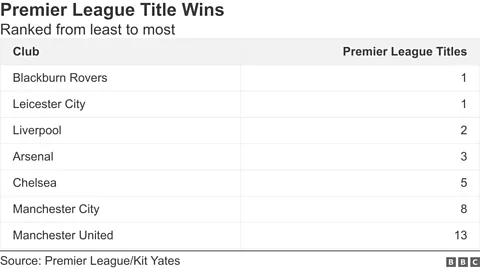赢得Premier League的俱乐部，按赢得的Premier League冠军数量从少到多排列 (Credit: BBC) 赢得Premier League的俱乐部，按赢得的Premier League冠军数量从少到多排列 (Credit: BBC)

在没有经过训练的人看来，这个序列可能并不重要。但这足以让许多数学爱好者感到兴奋。他们会认出这就是Fibonacci数列，其中每个数字（在前两个之后）都是序列中前两个数字之和。

这个数列可以在惊人的许多地方找到——从向日葵头部的种子螺旋排列和松果的苞片，到某些动物的家谱模式。

Fibonacci数列（复数形式，因为从不同的初始数字对开始，并遵循将连续数字相加来生成下一个数字的规则，会得到一个不同的，但相关的序列）最早由比萨的Leonardo在 1202 年引入欧洲科学，他也以他的昵称 Fibonacci（意思是 Bonaccio 之子）而闻名。

然而，早在 Fibonacci 在他的书 Liber Abaci 中推广这些数列之前，印度数学家就已经知道这些数列了。他们利用这些数列来帮助他们列举给定长度的诗歌的数量，使用一个单位长度的短音节和两个单位长度的长音节。印度诗人/数学家知道，你可以通过取一首长度为 n-1 的诗并添加一个短音节，或者取一首长度为 n-2 的诗并添加一个长音节来创作一首长度为 n 的诗。因此，他们发现，要计算出给定长度的诗歌的数量，你只需要将短一个音节的诗歌的数量加上短两个音节的诗歌的数量——这正是我们今天用来定义 Fibonacci 数列的规则。

隐藏在这些数列中的是另一个重要且相关的数学支柱——黄金比例。随着 Fibonacci 数列中的项变得越来越大，每一项与前一项的比率越来越接近黄金比例——小数点后几位近似为 1.61803。据推测，黄金比例控制着某些植物物种茎上叶子的排列，并且据称在艺术、建筑 和音乐中应用时，会产生令人赏心悦目的结果。

Fibonacci 数列经常被数学家们认为是数学之美的典范。它们可以提供生动的视觉例子，将数学写进现实世界的模式中，没有这些例子，许多非数学家很难理解我们在我们学科中看到的优雅。然而，在我们过度热衷于劝诱的过程中，有一种诱惑是将 Fibonacci 数列或黄金比例视为某种包罗万象的自然法则，支配着跨越数量级的现象，从鹦鹉螺贝壳的螺旋形状到飓风的漩涡再到星系的弯曲手臂。

实际上，尽管这些自然特征在美学上令人愉悦，但很少有特征符合 Fibonacci 数列的规则或表现出黄金比例。我们必须小心，不要试图将每个美丽的模式都塞进精致的 Fibonacci 玻璃鞋中——在没有因果关系的地方暗示因果关系并强加意义。

Getty Images Fibonacci 数列可以在各种自然现象中找到，包括向日葵的头部（Credit: Getty Images） Fibonacci 数列可以在各种自然现象中找到，包括向日葵的头部（Credit: Getty Images）

巧合？

因此，在像Premier League这样意想不到的地方发现 Fibonacci 数列的出现，真是非同寻常。当我们作为科学家，发现一个像这样的著名序列似乎凭空出现时，我们应该开始问自己，它是否告诉我们任何关于产生该序列的过程的重要信息。Premier League 冠军争夺战背后是否存在某种令人惊讶的看不见的过程，或者这仅仅是一个可爱的巧合？仅仅因为我们可以在某件事中看到 Fibonacci 数列，并不意味着它存在是有原因的。

尽管如此，发现这些看似巧合的东西对于科学发现的过程可能非常有用。例如，1912 年，Alfred Wegener 注意到一个明显奇怪的巧合，即西非的海岸线和南美洲的东海岸线似乎像拼图游戏中的碎片一样拼合在一起。尽管当时普遍认为，各大洲的巨大陆地太大而无法移动，但 Wegener 提出了唯一能够调和他的观察结果的理论。大陆漂移表明，这些陆地并没有固定在原地，而是可以非常缓慢地改变它们在地球表面的相对位置。

当 Wegener 在 1915 年发表他的理论时，他成了一个笑柄。地质学家驳斥了他古怪的想法，理由是缺乏移动如此巨大的地球表面块体的机制，并驳回了各大洲看似紧密的镶嵌结构，认为这纯粹是巧合。然而，到了 20 世纪 60 年代，板块构造理论——固体地幔和地壳在地球表面上的运动——为 Wegener 现在被广泛接受的理论提供了可信性。

Alamy 比萨的Leonardo——更广为人知的名字是 Fibonacci ——借鉴了在他之前的印度和伊斯兰数学家的工作（Credit: Alamy）

错误的进化

尽管巧合可以为新的科学发现指明方向，但当它们似乎证实了一个不正确的理论时，它们也可能成为科学进步的障碍。在 19 世纪初，德国解剖学家 Johann Friedrich Meckel 就犯了这样一个错误。他是 scala naturae（自然阶梯）的信徒，在自然阶梯中，人类在有秩序但静态的等级制度中高于所有其他动物。最简单、最原始的生命形式应该位于阶梯的最低等级，而最复杂和最先进的生物则位于最高等级。鉴于这种“存在巨链”是当时的主要理论，他的观点并不令人惊讶。现在普遍接受的“共同起源”理论——即多个物种起源于单一祖先群体——在当时还只是一个萌芽的想法。

Meckel 运用 scala naturae 来提出了关于他的专业领域——胚胎发育的猜想。被称为重演理论，他假定，随着高级动物（如哺乳动物）的胚胎发育，它们会依次经历与位于阶梯较低等级的“不太完美”的动物（如鱼类、两栖动物和爬行动物）非常相似的形式。该理论一个惊人但看似不太可能的预测是，随着人类经历“鱼类阶段”，他们的胚胎将具有鳃裂。

碰巧的是，1827 年发现人类胚胎在发育的早期阶段确实具有类似于鳃的裂缝。这一非凡的发现似乎证实了 Meckel 的预测并证实了他的重演理论。这种被认为的证据非常有力，以至于该理论被广泛接受，直到近 50 年后的 19 世纪 70 年代，重演理论才最终被抛弃，因为共同起源的观点开始占据主导地位。共同起源支撑着我们现在所知的现代进化论。它明确表示，子宫内的鳃裂远非经历“鱼类阶段”，而是因为我们与鱼类有共同的祖先，因此我们也共享了它们的大部分 DNA 和早期发育过程。

有时，巧合可能会误导科学家，表面上指向一个结论，而事实上，对于这些观察结果存在另一种解释，这种解释得到了事实的更好支持。

那么，在 Premier League 冠军头衔数量的数据中，出现美丽、几乎神秘的 Fibonacci 数列这一事实，对于这项美丽的运动意味着什么呢？由于没有可能产生该序列的合理机制，答案几乎肯定是什么都不意味着。

在这样一个不太可能的地方发现这个数学序列真是太棒了，这让我们有机会反思 Fibonacci 数的重要性。但是，模式并不总是意味着因果关系——巧合有时仅仅只是巧合。

而且，就像 Meckel 的鳃裂一样，它在 Premier League 记录中的出现仅仅如此——只不过是一个壮观但最终具有误导性的巧合。