他曾辍学成为诗人，如今荣获 Fields Medal 奖

作者：Jordana Cepelewicz

2022年7月5日

June Huh 在大学六年级时的一次偶然相遇后，才开始对数学产生兴趣。如今，他通过将组合数学和几何学联系起来的深刻见解，获得了数学领域的最高荣誉。

June Huh 在普林斯顿大学的办公室。 Caroline Gutman for Quanta Magazine

引言

作者：Jordana Cepelewicz 数学编辑

2022年7月5日

2022 Fields and Abacus Medals algebraic geometry combinatorics Fields Medal geometry graph theory mathematics polynomials profiles All topics (opens a new tab)

June Huh 经常迷路。每天下午，他都会在普林斯顿大学周围散步，他在该大学的数学系担任教授。在五月中旬的某一天，他正在穿过附近的高等研究院周围的树林——“只是想让你知道，”当他考虑前方道路的分叉时，他说，“我不知道我们在哪里”——并不时停下来，指出隐藏在树叶下或树后的野生动物的细微动静。在接下来的两个小时的漫步中，他发现了一对青蛙、一只红顶鸟、一只顶针大小的乌龟和一只动作敏捷的狐狸，每只动物都得到了他安静的观察时刻。

“我非常擅长发现东西，”他说。“这是我的特殊能力之一。”

39岁的 Huh 现已被授予 Fields Medal 奖，这是数学领域的最高荣誉，因为他有能力在数学领域中漫游，并找到恰到好处的对象——然后他使用这些对象，以新的、令人兴奋的方式，让看似不同的几何学和组合数学领域相互对话。从研究生院开始，他通过其他数学分支的迂回路线，深入每个证明的核心，解决了组合数学中的几个重大问题。Huh 说，每次找到这条路都像是“一个小小的奇迹”。

人们可能会对他的数学之路有同样的看法：它以漫游和一系列小奇迹为特征。年轻时，Huh 并不想成为一名数学家。他对这个科目漠不关心，并辍学成为一名诗人。他需要通过大学时代的偶然相遇——以及许多迷失的时刻——才能发现数学蕴含着他一直以来所寻找的东西。

本系列文章

2022 Fields and Abacus Medals

1. 在匮乏、战争与和平时期，一位乌克兰数学家发现了数学的魔力

2. 他曾辍学成为诗人，如今荣获 Fields Medal 奖

3. 凭借其运动式的数学方法，荣获 Fields Medal 奖

4. 一位解决最难的简单素数问题的专家

5. 开发了一种理解沟通新方式的科学家

那个诗意的转折后来被证明对他数学的突破至关重要。他的同事说，他的艺术性体现在他发现其工作中心那些恰到好处的物体的方式上，以及他寻求在所做的每件事中寻求更深层意义的方式上。Federico Ardila-Mantilla是旧金山州立大学的一位数学家，也是 Huh 的合作者之一，他说：“数学家在很多方面都像艺术家，因为我们真的在寻找美。”“但我认为在他的情况下，这一点尤为明显。我真的很喜欢他的品味。他创造出美丽的东西。”

Ardila 补充说：“当我发现他在诗歌之后才接触数学时，我想，好吧，这对我来说很有意义。”

Huh 本人将艺术家和数学家进行了比较。他说，对于两者来说，“感觉你是在抓住已经存在的东西，而不是在你的脑海中创造出什么东西。”

辍学者

在任何一天，Huh 都会做大约三个小时的专注工作。他可能会思考一个数学问题，或者准备给一群学生讲课，或者为他的两个儿子安排医生的预约。“然后我就筋疲力尽了，”他说。“做有价值的、有意义的、有创意的事情”——或者做他不太想做的事情，比如安排那些预约——“会消耗你大量的精力。”

听他讲述，他通常无法控制自己决定在这三个小时内专注于什么。在 2019 年春季的几个月里，他所做的只是阅读。他感到一种重温他年轻时第一次接触到的书籍的冲动——包括罗马皇帝 Marcus Aurelius 的《沉思录》和德国作家 Hermann Hesse 的几部小说——所以他就是这样做的。“这意味着我没有做任何工作，”Huh 说。“所以这有点问题。”（不过，他后来已经接受了这个限制。“我过去试图抵抗……但我最终学会了屈服于那些诱惑。”结果，“我越来越擅长忽略截止日期。”）

Huh 最近一次讲座的笔记。 Caroline Gutman for Quanta Magazine

他发现，强迫自己做某事或定义一个具体的目标——即使是对他喜欢的事情来说——也永远行不通。他特别难以将注意力从一件事转移到另一件事。“我认为意图和意志力……被高估了，”他说。“你很少能用这些东西实现任何目标。”

自从他年轻时起，情况就是如此。他于 1983 年出生于加利福尼亚州，他的父母在那里完成了研究生学业。当 Huh 大约 2 岁时，全家搬到了韩国首尔。在那里，他的父亲教统计学，他的母亲教俄语语言和文学。

上学对他来说是痛苦的。他喜欢学习，但无法在课堂环境中集中精力或吸收任何东西。相反，他更喜欢自己阅读——在小学时，他狼吞虎咽地读完了关于生物的百科全书的全部 10 卷——并探索他家公寓附近的一座山。他很快就熟悉了它的每一个角落，但他仍然设法迷路，有一次甚至最终进入了一个因可能存在地雷而被限制的区域。

他尽最大努力避免数学。他的父亲曾经试图用一本练习册教他，但 Huh 并没有试图解决这些问题，而是从后面抄写答案。当他的父亲发现并撕下那些页面时，Huh 去了一家当地的书店，并在那里写下了答案。“他在那个时候放弃了，”Huh 说。

当他 16 岁，高中一年级（在韩国持续三年）时，他决定辍学写诗。他有点浪漫。“听完好的音乐后，我真的会哭出来，”他说。他写关于自然和他自己的经历。他计划在必须上大学之前的两年内完成他的杰作。“所以这没有发生，”他笑着说。

他发现写作过程太注重自我——对他来说，这种探索往往是痛苦和令人沮丧的。此外，正如他后来意识到的，“我想成为一个写出伟大诗歌的人，”他说。“我不想写伟大的诗歌。”现在他认为那个版本的自己几乎完全是个陌生人。

当他于 2002 年进入首尔国立大学时，他感到茫然。他曾一度对成为一名科学作家很感兴趣，并决定主修天文学和物理学。但他经常逃课，不得不重修几门课程。“我只是普遍迷失了，”他说。“我不知道我想做什么。我不知道我擅长什么。”

事实证明，他毕竟擅长数学——这是他完全偶然发现的。

真正的美

Huh 花了六年时间才毕业。在第六年，他选修了著名的日本数学家 Heisuke Hironaka 的一门课，Hironaka 于 1970 年赢得了 Fields Medal 奖。Hironaka 很有魅力，Huh 很快就被他吸引住了。

但吸引 Huh 的不仅仅是他的教授的魅力。这也是数学本身。表面上，这门课程是对代数几何的介绍，是对代数方程的解及其几何性质的研究。相反，Hironaka 教授了他自己在称为奇点理论的领域中的工作，该理论侧重于某些类型的空间。“基本上，他讲的是他昨天思考的东西，”Huh 说——一个非常特殊的问题，以及不一定正确的证明。最初有 200 名学生的班级迅速减少；几周后，只剩下五名学生，Huh 是其中之一。

他第一次亲眼目睹了研究数学的展开。Hironaka 的讲座不像其他本科课程那样经过润色，在其他本科课程中，一切都经过简化，答案已经解决了。Huh 喜欢这种悬念，喜欢尝试做一些没有人真正知道该怎么做的事情的行为——以及随之而来的自由，可能出现的惊喜。他说，大学里教授的典型材料经过了几个世纪的提炼。“这与在你眼前观察这种原始数学非常不同。”

Huh 在普林斯顿大学校园。 Caroline Gutman for Quanta Magazine

Huh 发现，这种数学可以给他诗歌无法给予的东西：在自身之外寻找美的能力，以一种比写作更能打开他的方式，试图掌握外部的、客观的和真实的东西。“你不会想到你渺小的自我，”他说。“没有自我的容身之地。”他发现，与他作为一名诗人不同，他从未受到获得认可的愿望的驱使。他只是想做数学。

Hironaka 或许认识到这一点，便把他收为门徒。在 Huh 毕业并开始在首尔国立大学攻读硕士学位后——在那里他也遇到了 Nayoung Kim，也就是他现在的妻子——他花了很多时间与 Hironaka 在一起。休息期间，他跟随教授回到日本，与他住在东京和京都，提着他的包，一起吃饭，当然也继续讨论数学。

意想不到的发现

Huh 申请了美国大约十几个博士课程。但由于他平庸的本科经历，他被所有课程拒绝了，只有一个例外。2009 年，他开始在伊利诺伊大学厄巴纳-香槟分校学习，然后在 2011 年转到密歇根大学完成他的博士学位。

尽管面临挑战——生活在一个新的国家，与 Kim 分开（她在首尔国立大学攻读数学博士学位）——Huh 珍惜他在研究生院的经历。他能够全身心地投入到数学中，并且享受了探索的自由，正是这种自由首先吸引了他。

他立刻脱颖而出。作为伊利诺伊州的一名刚入门的研究生，他证明了图论中的一个猜想，这个猜想已经悬而未决 40 年了。以最简单的形式来说，这个问题被称为 Read 猜想，涉及与图相关的多项式——类似于 n 4 + 5 n 3 + 6 n 2 + 3 n + 1 这样的方程式，图是由顶点（点）通过边（线）连接而成的集合。特别是，假设您想要为图的顶点着色，以使没有两个相邻的顶点具有相同的颜色。给定一定数量的颜色供您使用，有很多方法可以为该图着色。事实证明，可以使用称为色多项式的方程式（以正在使用的颜色数量表示）来计算可能性的总数。

数学家观察到，无论图是什么，色多项式的系数似乎总是服从某些模式。首先，它们是单峰的，这意味着它们先增加然后减少。以前面的多项式为例。其系数的绝对值——1、5、6、3、1——形成一个单峰序列。此外，该序列也是“对数凹”的。对于序列中的任何三个连续数字，中间数字的平方至少与两侧项的乘积一样大。（例如，在上面的多项式中，62 ≥ 5 × 3。）

Merrill Sherman/Quanta Magazine

尽管如此，数学家们仍在努力证明这些性质。然后，Huh 似乎凭空出现。

作为一名硕士生，他曾与 Hironaka 一起研究代数几何和奇点理论。该领域的主要研究对象称为代数簇，可以将其视为由某些方程式定义的形状。有趣的是，与某些类型的代数簇相关联的数字已知是对数凹的——Huh 只知道这一点是因为他的研究偶然地转向了正确的方向。Huh 的关键思想是找到一种方法来构造一个代数簇，使得那些相关的数字恰好是原始问题中图的色多项式的系数。

他的解决方案震惊了数学界。正是在那时，密歇根大学拒绝了他的初步申请后，招募他进入了他们的研究生课程。

Huh 的成就令人印象深刻，不仅因为他解决了 Read 猜想，而此前该猜想似乎完全难以解决。他表明，在图的组合性质之下潜藏着更深层次的——并且是几何的——东西。

数学家们也对他的风度印象深刻。他在会议上的演讲总是平易近人且具体；与他交谈时，很明显他正在深入而广泛地思考他正在研究的概念。Matthew Baker是佐治亚理工学院的一位数学家，他说：“对于一个研究生来说，他成熟得令人难以置信。”在 Baker 第一次见到他之后，“我就想，这个人是谁？”

Mircea Mustaţă是 Huh 在密歇根大学的导师，据他说，他几乎不需要任何监督或指导。与大多数研究生不同，他已经心中有了一个计划，并且对如何执行它有自己的想法。“他更像一位同事，”Mustaţă 说。“他已经有了自己看待事物的方式。”

他的许多合作者都注意到他非常谦逊和脚踏实地。当他得知自己获得了 Fields Medal 奖时，“感觉并不是很好，”Huh 说。“当然你很高兴，但在内心深处，你有点担心他们最终可能会发现你实际上并没有那么好。我是一位相当不错的数学家，但我配得上 Fields Medal 奖吗？”

逃离空间

图实际上只是可以定义更一般结构的对象的类型之一，这些结构称为拟阵。例如，考虑二维平面上的点。如果两个以上的点位于该平面上的一条线上，则可以说这些点是“相关的”。拟阵是抽象对象，可以捕捉各种不同上下文中的依赖和独立等概念——从图到向量空间再到代数字段。

Merrill Sherman/Quanta Magazine

正如图具有与之相关的色多项式一样，也有称为特征多项式的方程式与拟阵相关联。有人推测，这些更一般对象的多项式也应该具有对数凹的系数。但是 Huh 用来证明 Read 猜想的技术仅适用于显示非常狭窄的拟阵类的对数凹性，例如来自图的拟阵。

在数学家 Eric Katz 的帮助下，Huh 扩大了拟阵的类别，以使这样的证明可以应用。他们遵循了一种类似的方法。与以前一样，该策略是从感兴趣的对象（此处为拟阵）开始，并使用它来构造代数簇。从那里，他们可以提取一个称为上同调环的对象，并使用它的一些属性来证明对数凹性。

只有一个问题。大多数拟阵没有任何几何基础，这意味着实际上没有代数簇可以与它们相关联。相反，Huh、Katz 和数学家 Karim Adiprasito 想出了一种方法，可以直接从拟阵中，基本上是从头开始写出正确的上同调环。然后，他们使用一组新技术表明，它的行为就像它来自实际的代数簇一样，即使它不是。通过这样做，他们证明了所有拟阵的对数凹性，并一劳永逸地解决了称为 Rota 猜想的问题。“它能奏效真是太了不起了，”Baker 说。

这项工作表明，“你不需要空间来做几何，”Huh 说。“这让我从根本上重新思考了几何是什么。”它还将引导他解决许多其他问题，在那里他继续进一步推进这个想法，使他能够开发出更广泛的方法。

但是，尽管这项工作需要一定的针对性，但构建正确的上同调环需要大量的猜测和在黑暗中摸索。这是 Huh 特别喜欢这项工作的一个方面。“没有指导原则……没有明确定义的目标，”他说。“你只需要做一个猜测。”

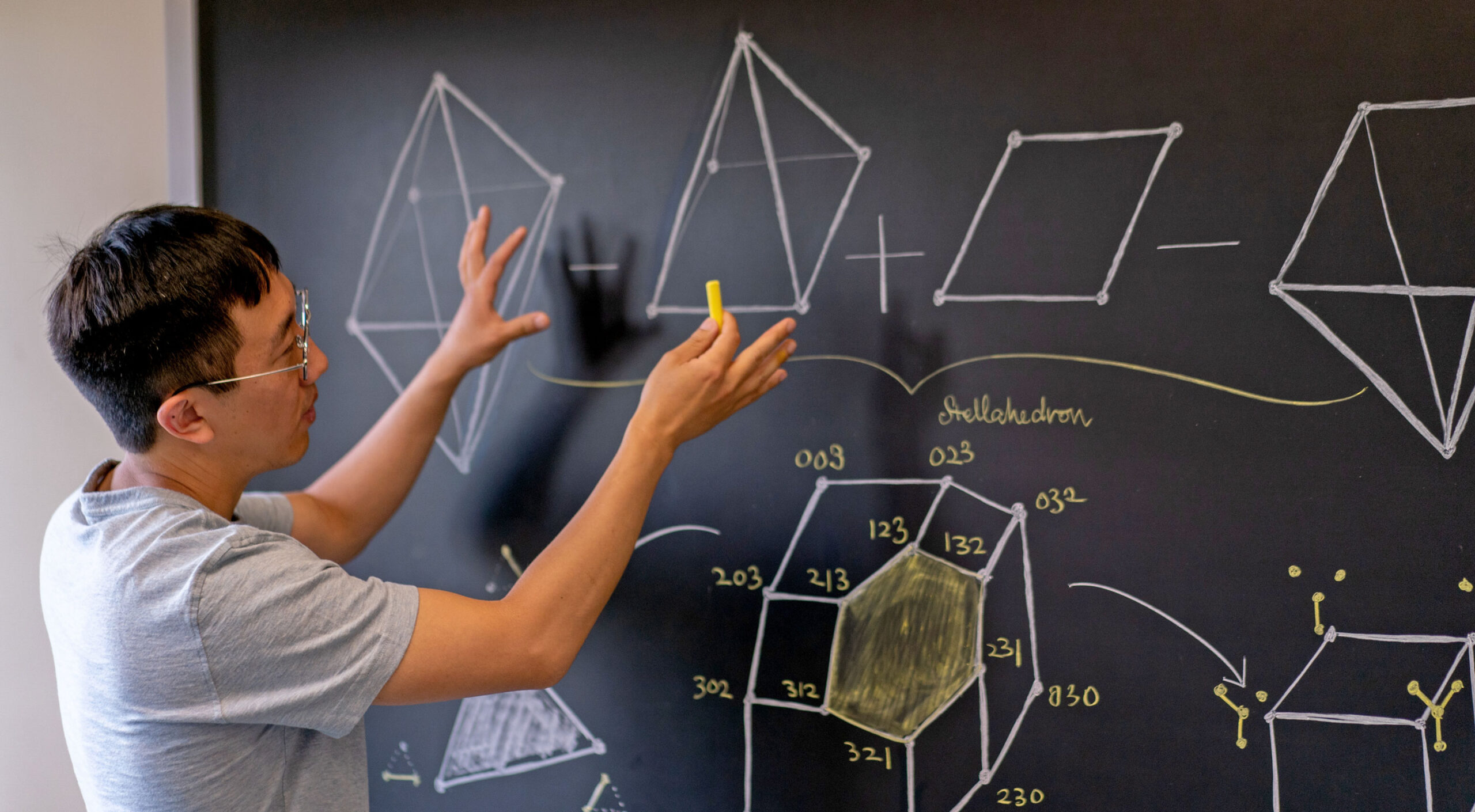Huh 的工作涉及调查拟阵的性质。这些抽象结构有时可能来自几何对象。 Caroline Gutman for Quanta Magazine

这种缺乏意图的情况恰恰反映了他如何在日常生活中发挥最佳作用。这似乎是他发现了一个与他的个性完美契合的数学程序。Huh 再次发现，“事情只是自己发生，”他说。

事物的核心

Huh 说话缓慢，经常停顿并仔细选择他的措辞，并且以一种平静、平和的方式进行，这种方式接近冥想。威斯康星大学麦迪逊分校的数学家 Botong Wang 说：“他不太容易激动。”

他在做数学时也以同样的方式进行。他与 Huh 在许多重要的最新成果上进行了合作。Wang 第一次亲眼目睹时感到震惊。“我有一种数学竞赛的经验，那就是作为一名数学家，你必须聪明，你必须快，”他说。“但 June 正好相反。……如果你和他谈论五分钟关于一些微积分问题，你会认为这家伙无法通过资格考试。他非常慢。”事实上，他非常慢，以至于起初 Wang 认为他们正在将大量时间浪费在他们已经理解的简单问题上。但他后来意识到，Huh 正在以一种更深入的方式学习看似简单的概念——并且正是这种方式后来被证明是有用的。

Graham Denham是安大略省西安大略大学的一位数学家，也是 Huh 的合作者之一，他说：“June 喜欢以正确的方式做事。”

例如，Denham、Ardila 和 Huh 刚刚完成了一个 50 页的证明，该证明与 Rota 猜想密切相关，这时 Huh 说他们应该花更多时间来找到一种更简洁、更吸引人的方法。他认为有一个更好的解释，最好不要操之过急。“Federico 和我想，哦，好的，那我们就把它扔掉吧，好吗？”Denham 说。

花了两年时间来制定更好的论点。“很高兴我们都获得了终身教职，”Ardila 说。不过，最终，Ardila 和 Denham 都同意额外的努力是值得的。他们的最终结果“完全不同，更深入，并且[触及了]事物的核心，”Ardila 说。

Huh 保留了一小部分多面体——具有平面边的几何对象。 Caroline Gutman for Quanta Magazine

这种方法不仅适用于 Huh 的数学工作。2013 年，他决定要学习做饭。作为一名完全的初学者，他采取了每天做同一道菜的策略——一道简单的油拌面——直到它完美为止。六个月来，他完全按照这个方法做。（据 Kim 说，到目前为止，这是他唯一会做的菜。）

Huh 的整个生活都是建立在规律之上的。“几乎我所有的日子都完全一样，”他说。“我对重复的容忍度很高。”他很难保持睡眠，通常在凌晨 3 点左右醒来。然后他去健身房，与他的妻子和两个儿子（一个 8 岁，另一个刚满 1 岁）一起吃早餐，然后送他的大儿子去上学，然后再去他在普林斯顿的办公室。

办公室很空旷，几乎空无一物。有一张大桌子，一张用来睡觉的沙发——Huh 通常在早上晚些时候午睡——以及一张铺在地板上的瑜伽垫（他说，只是用来躺着；他实际上不知道如何做瑜伽）。没有书，只有几堆纸张整齐地排列在靠墙的架子上。角落里有一台吸尘器。Huh 喜欢重复的、没有脑力的活动，如清洁、洗碗和将他阅读的内容抄写到笔记本中的体力活动。

他经常在公共图书馆的儿童区工作，那里非常吵闹。“我不喜欢安静的地方，”他说。“这让我昏昏欲睡。”Huh 对很多事情都这么说。

他每天午餐后都会长时间散步，然后返回办公室做更多的工作（除非他已经达到了他的三个小时的配额），然后再回家。他将剩下的晚上与家人共度；他们都在晚上 9 点左右一起睡在一张大床上。

这种对规律的偏爱——以及对任何偏离规律的事物感到疲惫的倾向——有时会以极端的方式表现出来。例如，当他在密歇根州完成博士学位时，“我会切断几乎所有其他东西，”Huh 说。当他第一次搬到安娜堡时，他发现自己没有为严酷的冬天做好准备。他几乎没有什么财产，并且需要一条毯子。但是，当他查阅如何去当地购物中心时，他发现这在后勤上太困难了。“这超出了我的容忍程度，”他说。“我不想浪费我的精神能量来弄清楚如何从这里到那里。”相反，他走到附近的一家 CVS 药店，买了 10 块布料和一个巨大的订书机，然后用订书机将这些布料订在一起做成一条毯子。

Huh 在普林斯顿的路易斯科学图书馆。 Caroline Gutman for Quanta Magazine

他靠冷冻披萨生活了好几个月，因为他不想处理购买食物和烹饪的问题。他只是想做数学。他将他生命中的那个时期描述为“几乎是修道士般的”。事实上，当时，他真的只与另一个人——他的导师 Mustaţă——每周交谈一次。

Kim 回忆起 Huh 还在伊利诺伊州时去拜访他，“在那之后，我真的重新思考了我们的关系，”她说。“我应该嫁给他吗？因为他[不能]处理现实生活技能，生存技能。”

然而，她在 2014 年嫁给了他。他们搬到了普林斯顿，在那里他们都开始在高等研究院工作。这是 Kim 第一次住在美国，她不习惯用英语处理某些任务；她不得不依靠 Huh 来完成任务。“让我们这么说吧，她很失望，”他说。

那年晚些时候，Kim 生下了他们的第一个儿子 Dan。在分娩时，她发现 Huh 正在做数学。

“我的妻子比我更平衡，”他说。“生活有很多方面，而数学只是其中非常、非常、非常小的一部分。”

“我是一个真正的工作者，”Kim 说。“他是一个思考者。”

但是，她补充说，从那时起，Huh 已经大大改善了。随着这对夫妇抚养 Dan，“我学会了如何过上更平衡的生活，”Huh 说。“那是一个变革时期。”他花了很多时间与 Dan 在一起——与他一起绘画，解决 Dan 为他创建的复杂的数学练习册中的问题，并带他去书店和其他当地景点。他甚至处理 Kim 要求他做的后勤任务，尽管很不情愿。“我仍然不喜欢它，”他说，“但我的意思是，我们不能只靠订书机订的毯子生活。”

现在他甚至能够摆脱数学。当他处于闲置状态时，他的头脑不再回到解决问题，当其他事情需要他时，他能够休息一下。

“他完全变了一个人，”Kim 说。

顶部沉重

无论如何，有些事情没有改变。Huh 仍然只能集中精力每天工作几个小时。“其他人工作一个小时，只休息五分钟，”Kim 说。“他就像，一个小时做其他事情，然后只专注于五分钟、十分钟。”

他对美的追求也没有改变。而且，他经常回到关于对数凹性或类似概念的问题，以此来挖掘那种美。

Caroline Gutman for Quanta Magazine

例如，他和 Wang 以及其他合作者最近证明了一个关于点、线和平面配置的基本问题，称为 Dowling-Wilson “顶部沉重”猜想。考虑平面上点的有限集合，其中每对点都通过一条线连接。数学家 Paul Erdős 和 Nicolaas Govert de Bruijn 表明，线的数量必须始终大于或等于点的数量（除非所有点都位于一条线上）。例如，考虑排列在正方形角上的四个点。线描绘出正方形，并且连接相对的角，总共加起来有六条线。

顶部沉重猜想推广了这个想法。不是在平面上，而是给您一个高维空间中的一组点。考虑所有连接点对的线、由三点集合跨越的平面、由四点构造的三维子空间等等。现在考虑一个由这些数字构建的序列：点的数量、线的数量、平面的数量。比较该序列中对称位置的数字（第一个和最后一个数字、第二个和倒数第二个数字，依此类推）。对应于更高维空间的数字将至少一样大——也就是说，该序列是顶部沉重的。（还推测该序列是对数凹的，但这尚未得到证实；到目前为止，Huh 和 Wang 已经表明该序列的前半部分是单峰的。）

Merrill Sherman/Quanta Magazine

Huh 和 Wang 改编了 Huh 在 Rota 猜想中所做工作中的想法，但这样做他们不得不进一步推进他的计划。同样，他们正在处理拟阵、代数簇和上同调环。但是这一次，他们必须找到的代数簇涉及奇点，这些奇点是当您放大某个空间时，它看起来与其他点不同的地方。这使得构建正确的空间并证明关于其上同调环的某些性质变得更加复杂——甚至更难以解决他们必须直接从拟阵构建这些环，而没有代数簇来指导他们的情况。

在他们花费五年时间解决这个问题期间，Huh 也开始研究一种完成与几何的决裂的方法。在那之前，他的大部分工作都涉及构建问题所需的精确上同调的艰巨任务。此外，一旦找到上同调，数学家们仍然必须证明它满足某些性质，这可能也需要数年时间。

Caroline Gutman for Quanta Magazine

他开发的新理论（与数学家 [Petter Brändén](https://www.quantamagazine.org/june-huh-high-school-dropout-wins-the-fields-medal