andersource postsaboutprojectsworkshopsRSS 🎗️

不平衡学习与类别权重调整的探索之旅：Class Weight 重要吗？

最终的突破

2025年5月5日

几个月前，我正在处理一个图像分类问题，这个问题的类别严重不平衡——正类比负类少得多。

在模型调优阶段，我想探索类别不平衡的影响并尝试缓解它。一个流行的“现成”解决方案是对类别进行加权，权重与它们的频率成反比——但这并没有带来改进。过去我遇到过好几次这种情况，除了基本的直觉之外，我无法追溯这种加权背后的理论依据（也许我没有足够努力）。

因此，我决定最终尝试从第一性原理来推理不平衡设置中的类别加权。以下是我的分析。TL;DR 的结论是，对于我的问题，我确信类别加权可能并不重要。

这是一个有趣的分析，也是一个有趣的探索，但它做出了很多假设，我建议谨慎对待，不要过度概括。

权衡

只要存在（非平凡的）分类问题，就存在权衡。我将重点关注最简单的二元分类情况：假设我们有两个类——负类（表示为 0）和正类（表示为 1）；进一步假设正类是稀有类，其流行度为 β（在以下可视化/实验中为 1%）。

基本上，当我们进行分类时，我们会预测一个未知类别的实例的类别。我们可能会在两个方面犯错：

  1. 将负实例分类为正实例（假正例）
  2. 将正实例分类为负实例（假负例）

避免任何一种错误都很容易：例如，我们可以将所有实例分类为负例，从而完全避免假正例（代价是所有正例都变成假负例）。这就是权衡所在：要创建一个输出“硬”预测的实际分类器，我们需要就每种错误的严重程度做出产品/业务决策。不做出明确的决定意味着我们的优化流程已经隐式地做出了这样的选择。

现在，很难预先知道权衡曲线会是什么样子。我们尝试优化所有其他因素，以提供最佳的选项集：收集大量具有信息性特征的数据，使用合适的模型等等。但在完成所有这些之后，我们仍然需要选择如何平衡两种类型的错误。

为了根据我们的产品偏好优化这个选择，我们首先需要表征权衡曲线。

表征权衡曲线

首先是一些定义：

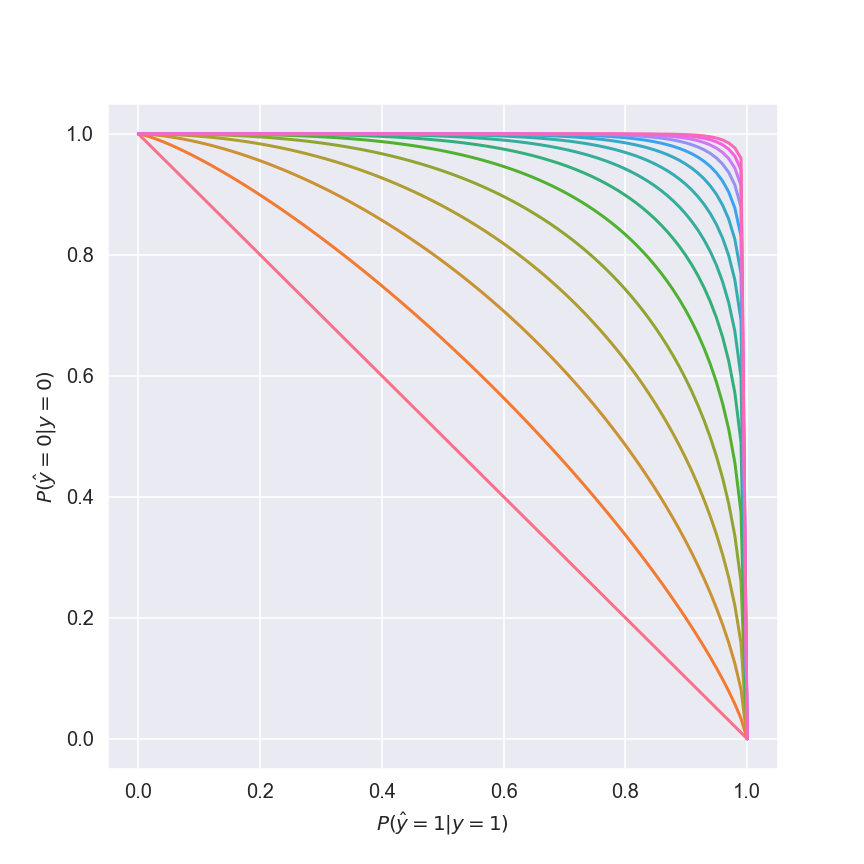
为了便于分析，我假设权衡曲线的形式为 z=(1−xp)1p, 其中 p≥1。这产生以下曲线族： 假定的正/负检测概率之间权衡的性质

红色曲线对应于 p=1——一个非常糟糕的权衡曲线。随着我们增加 p，我们的选项集会得到改善。在令人向往的（但实际上无法实现的）p=∞ 时，我们会选择 x=z=1，彻底解决问题然后回家；在此之前，我们必须在 x 和 z 之间做出一些妥协。

稍后，我们将思考_如何_选择权衡。但要做到这一点，我们首先需要定义我们甚至想要优化的是什么。

表明立场

正如我之前提到的，初始建模阶段会尝试为我们提供任务的最佳权衡曲线——使用数据、模型类型、训练技术等等。在这些阶段，我们可以针对与阈值无关的指标进行优化，例如各种 曲线下面积 指标。但最终，在某个下游，模型的输出将被二值化，我们不妨在调整模型时考虑到这一点。

我个人喜欢 F-score——它结合了两个非常容易解释的指标（精度和召回率），这使得与技术性较低的利益相关者（例如产品经理和 FDA）进行沟通变得更容易，并且可以 轻松调整以考虑误差类型偏好。

对于这个问题，精度和召回率同样重要，所以我使用了 F1 分数： F1=21precision+1recall

最终，这就是我们想要优化的指标。

控制旋钮在哪里？

好的，所以我们知道我们想要优化什么，并且我们知道我们的选择受到权衡曲线的限制。但是我们如何控制我们落在曲线上的位置呢？

规范上，二元分类被定义为最小化 二元交叉熵损失。我们将使用权重系数 α 作为决定我们落在权衡曲线上哪个位置的旋钮，用于正例： BCE=−∑iαyilog2⁡yi^+(1−yi)log2⁡(1−yi^))

优化

现在所有的参与者都在舞台上，让我们卷起袖子，开始动手吧。

首先，我们将从查看单个实例退一步，并根据 β（正类流行度）查看正实例和负实例之间的关系。为此，我们将用它们各自的期望值 x 和 z 替换单个 yi^ 和 1−yi^ 。此外，我们假设的权衡曲线将一个变量限制为另一个变量；让我们将损失重新定义为 x 的函数（也取决于 α、β 和 p。）

BCE(x)=−(αβlog⁡x+(1−β)log⁡(1−xp)p)

现在我们将对 x 求导，以找出我们对 α 的选择以及 β 和 p 的实际情况让我们落在了权衡曲线的哪个位置： BCE′(x)=−(αβxln⁡2+1−βp⋅1(1−xp)ln⁡2⋅(−pxp−1))= =(1−β)xp−1(1−xp)ln⁡2−αβxln⁡2 BCE′(x)=0⇔(1−β)xp=αβ(1−xp)

我们最终得到： x=αβαβ−β+1p

中场休息回顾

我们已经得到一个以 β 和 p 为特征的二元分类问题。我们使用加权二元交叉熵优化了一个分类器，其中正例（稀有类）的权重为 α。这使我们落在了权衡曲线上的特定位置，我们刚刚找到了（这些是 x 和 z）。

接下来，我们想看看我们对 α 的选择如何向下影响 F1 分数，并使用此描述来找到 α 的最佳值。

计算 F1

我们有兴趣计算我们选择 α 所产生的预期 F1 分数。由于 F1 直接取决于精度和召回率，我们将计算这些指标的期望值。

召回率很容易——它是我们正确检测为正例的正例的比例，我们可以期望它为 x——我们的分类器为正例输出 1 的概率。

精度是 truepositivestruepositives+falsepositives 的比例。

预期的真正例是正例的比例乘以将正例检测为正例的概率：βx。

预期的假正例是错误分类的负例：(1−β)(1−z)。

将所有这些放入 F1 公式中： E(F1)=2βx+(1−β)(1−z)βx+1x=2βxβx+βz+1−z

虽然 α 没有在此处显式显示，但它是 x 和 z 的一部分，我们知道它们并且确实出现在此处。

太棒了！所以剩下的就是对 α 求导并找到最大值，对吧？ 2β(αβαβ−β+1)1p((1−β)(((αβαβ−β+1)1p)p−1)2(β(αβαβ−β+1)1p+β(1−((αβαβ−β+1)1p)p)1p−(1−((αβαβ−β+1)1p)p)1p+1)+(β−1)(β(αβαβ−β+1)1p(((αβαβ−β+1)1p)p−1)2−β(1−((αβαβ−β+1)1p)p)p+1p((αβαβ−β+1)1p)p+(1−((αβαβ−β+1)1p)p)p+1p((αβαβ−β+1)1p)p))αp(((αβαβ−β+1)1p)p−1)2(αβ−β+1)(β(αβαβ−β+1)1p+β(1−((αβαβ−β+1)1p)p)1p−(1−((αβαβ−β+1)1p)p)1p+1)2

额，哈哈，没关系，让我们用数值方法来解决。

这是预期 F1 作为 α 函数的图，适用于一系列 p 值。

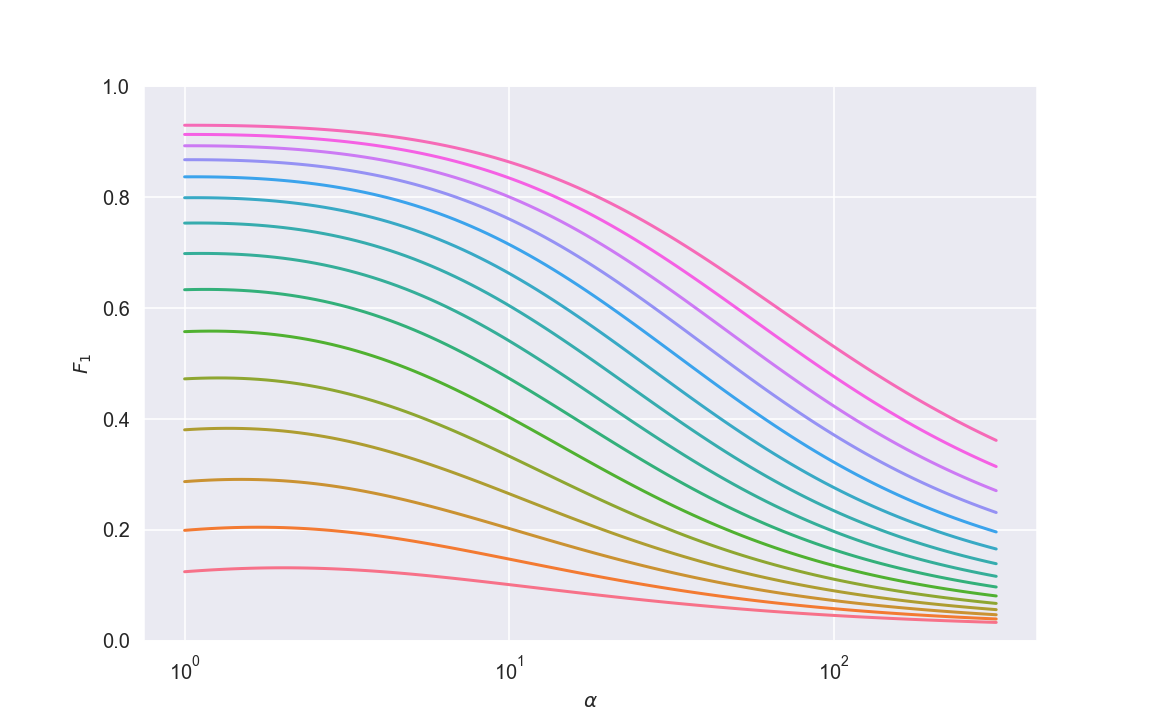
α 对不同 p 值下的 F<sub>1</sub> 分数理论影响

红色曲线对应于 p≈2，并显示出非常糟糕的结果；随着 p 的增加，我们得到越来越好的结果。

α 的范围从 1（相当于未加权训练）到大约 250，其中 100 是“反比例”加权的做法。

最突出的是，我们看到_类别权重几乎没有比未加权训练更好_，并且最佳权重通常_仅比未加权版本略大_，并且远非反比例。事实上，从这些图中可以看出，使用反比例加权方案实际上对训练有害！

确实很有意思。

注意事项和限制

记住我们为了到达这里做出了很多假设是件好事。特别是以下几件事可能会限制结论的范围：

理智检查

我想了解一下这些结论在无菌数学环境之外的普遍性。我使用 scikit-learn 的 make_classification 和 DecisionTreeClassifier 设置了一个基本的类别不平衡分类管道，并创建了上述图的经验版本，使用 class_sep 作为权衡曲线的代理。

该设置中的几件事与我干净的假设有很大不同，我很想看看结果。我让我的计算机运行了几个小时（运行了数十万次模拟），它产生了以下图：

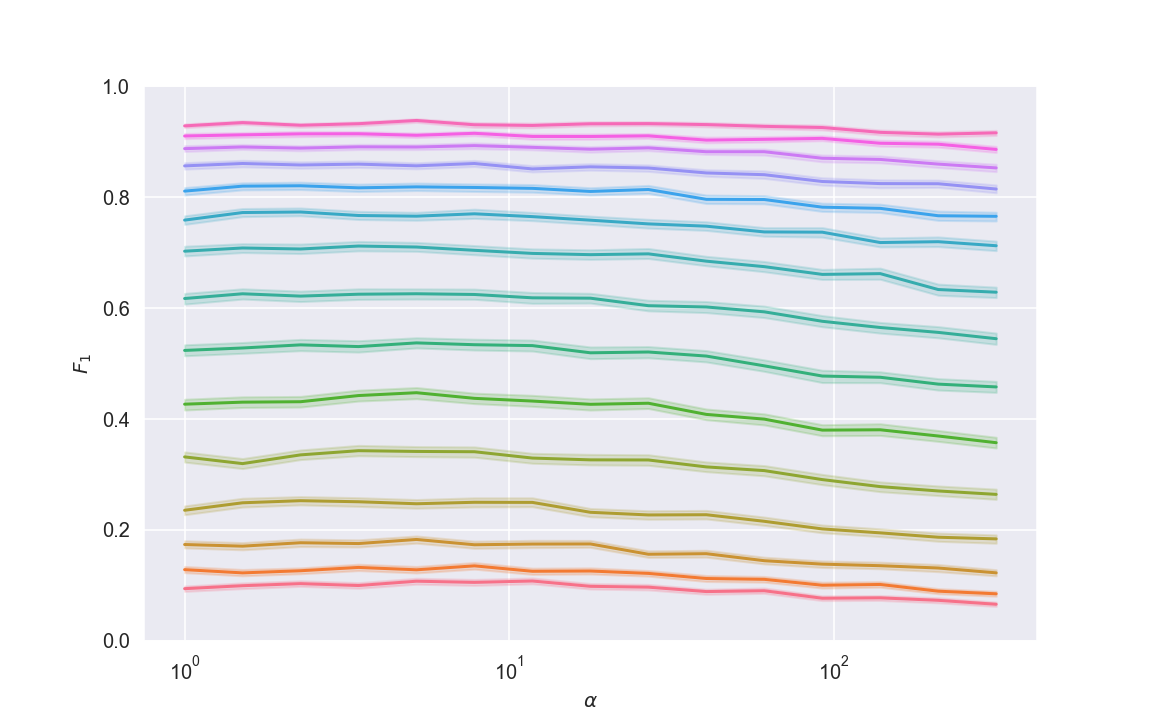
α 对不同 p 值下的 F<sub>1</sub> 分数的经验影响

不错！它与理论推导的图并不完全相同，但看起来非常相似，特别是：

至于为什么对于较大的 α 值图看起来不同，我的预感是权衡曲线不是对称的，这使得分类器能够在不完全牺牲精度的情况下获得不错的召回率。

结论

虽然我现在肯定不了解关于类别加权的一切，但我对分析非常满意：我知道类别不平衡_本身_并不能保证使用类别权重。此外，如果我认为类别权重是必要的，那么与其使用典型的“反比例”方案，不如说我的权重最好通过特定的问题特征来了解：权衡曲线的性质、标签噪声以及我分配给每种误差类型的成本。

更新 2025/08/05

在发布这篇文章后，有人向我指出，有一些教程专门演示了反比例加权（或分层欠采样/过采样，它们几乎等效）如何提高类别不平衡分类的性能。这引起了我的兴趣，我查看了这样一个教程，并发现了一些非常有趣的东西。为了衡量性能，该教程使用了 平衡准确率分数 而不是 F1。

F1 是正精度和正召回率的 调和平均值；平衡准确率是正召回率和负召回率之间的（常规）平均值。从表面上看，这两个指标看起来足够相似：每个指标本身都是两个指标的组合，对应于我们可以犯的两种类型的错误。

但是，与往常一样，细节很重要。我使用了与之前相同的优化框架，但查看了预期平衡准确率（而不是预期 F1）作为类别权重的函数，这就是我得到的：

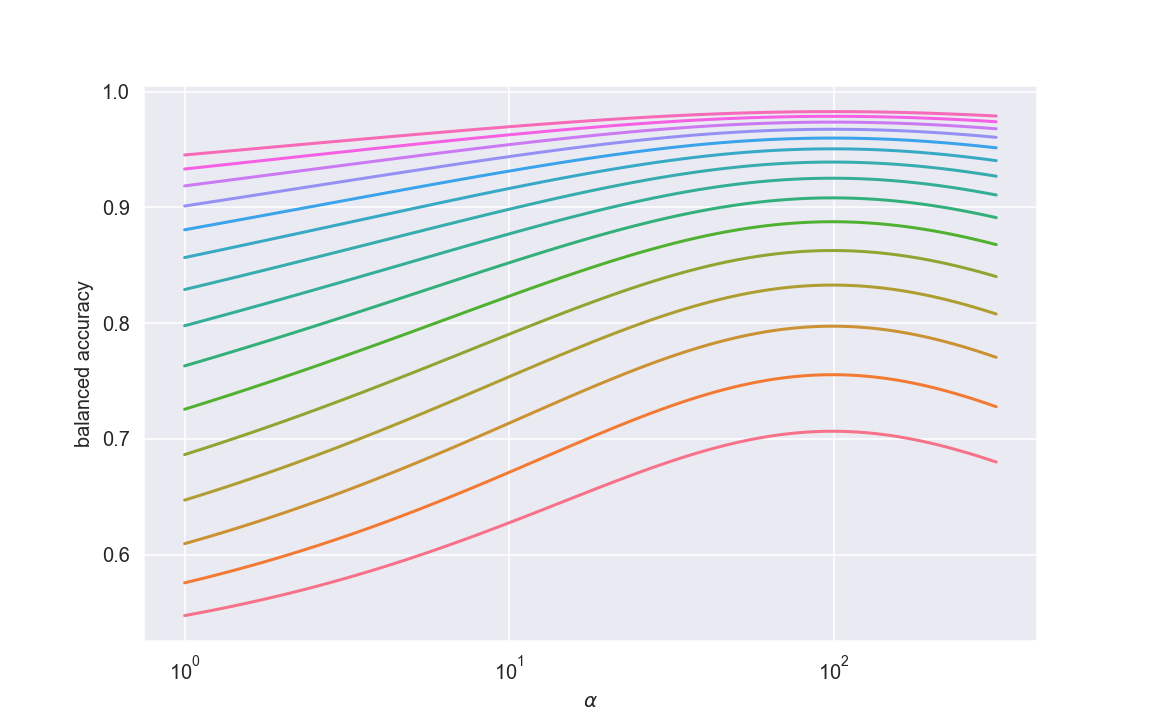
α 对不同 p 值下的平衡准确率分数理论影响

看看——与 F1 行为完全不同！此外，最佳权重_确实是反比例经验法则_。这非常棒：理论方法与人们在实践中获得的结果一致。更少地从个人利益出发，它确实突出了指标选择对模型调优的重要性——不同的指标对我们超参数的选择反应非常不同。

F1 与平衡准确率

让我们深入研究这两个指标之间的差异，以便我们对选择哪个指标有一个直观的了解。具体来说，我们将寻找一个它们彼此非常不同的场景。

想象一下我们有 1000 个样本——10 个正样本，990 个负样本。我们将所有正例分类为正例，将 40 个负例分类为正例。正召回率是完美的（100%），负召回率是 950990≈ 96%，正精度是 1050= 20%。平衡准确率会非常高，但 F1 会非常低。

这是一个不同指标引发对两种类型误差的不同偏好的示例。这里没有绝对的对与错——这是一个将您的技术选择与领域对齐的问题。

结论（再次）

对我来说，这再次强调了考虑模型的下游用途的重要性，并在为硬预测调整模型时咨询业务利益相关者。

代码

可视化和模拟的代码可以在 这里 找到。

相关

在此处注册以获取有关新帖子的更新： 感谢您的订阅！

实验与思考 © andersource 2019 - 2025