Block Diffusion：插值自回归和扩散语言模型

Block Diffusion: Interpolating Autoregressive and Diffusion Language Models

Source | HN Comments

该研究提出了Block Diffusion语言模型，它结合了自回归模型和扩散模型的优点。Block Diffusion通过在离散去噪扩散模型和自回归模型之间插值，实现了高质量、任意长度的序列生成，并支持KV缓存和并行化。研究通过高效的训练算法和数据驱动的噪声调度，解决了扩散模型在似然建模和固定长度生成方面的局限性，并在语言建模基准测试中取得了新的进展。

Block Diffusion：插值自回归和扩散语言模型

Marianne Arriola1, Aaron Gokaslan1, Justin Chiu2, Zhihan Yang1, Zhixuan Qi1, Jiaqi Han3, Subham Sahoo1, Volodymyr Kuleshov1 1Cornell 2Cohere 3Stanford ICLR 2025 Oral Paper Code Hugging Face HuggingFace

自回归 (Autoregression) : ✅ 高质量 ✅ 任意长度 ✅ KV缓存 ❌ 不可并行化

扩散 (Diffusion) : ❌ 较低质量 ❌ 固定长度 ❌ 无KV缓存 ✅ 可并行化

Block Diffusion : ✅ 高质量 ✅ 任意长度 ✅ KV缓存 ✅ 可并行化

摘要

扩散语言模型相比于自回归模型，在并行生成和可控性方面具有独特的优势，但在似然建模方面落后，并且仅限于固定长度的生成。在这项工作中，我们引入了一类 Block Diffusion 语言模型，它在离散去噪扩散模型和自回归模型之间进行插值。Block Diffusion 通过支持灵活长度的生成，以及通过 KV 缓存和并行 token 采样提高推理效率，克服了这两种方法的关键限制。我们提出了一种构建有效的 Block Diffusion 模型的方案，包括高效的训练算法、梯度方差估计器和数据驱动的噪声调度，以最小化方差。Block Diffusion 在语言建模基准测试中树立了扩散模型的新标杆，并能够生成任意长度的序列。

自回归 vs. 扩散语言模型

在语言建模任务中，我们有一系列从数据分布 q(x) 中抽取的 L 个 token x=(x1,…,xL)。我们的目标是拟合一个 q 的模型 pθ(x)。自回归模型定义了一种形式的分解分布： log⁡pθ(x)=∑ℓ=1Llog⁡pθ(xℓ∣x<ℓ) 然而，token 之间的顺序依赖关系要求 AR 采样被限制在 L 个采样步骤中，这对于长序列来说可能很慢。扩散模型通过独立地建模 token 来克服这一限制，从而允许并行生成。扩散模型改为拟合一个模型，以使用转移矩阵 Qt 来撤消前向损坏过程 q(xt|xt−1)=Cat(xt;Qtxt−1)。D3PM (Austin et. al) 将此定义为 pθ(xs|xt)=∏ℓ=1Lpθ(xsℓ|xt)=∑x[q(xsℓ|xtℓ,xℓ)pθ(xℓ|xt)] 其中去噪基本模型 pθ(xℓ|xt) 预测给定噪声 token xt 的干净 token xℓ。然而，扩散目标最小化了似然的界限。因此，扩散模型在似然性和样本质量方面落后。此外，扩散模型被限制为生成固定长度的序列。

BD3-LMs：Block Discrete Denoising Diffusion Language Models

我们结合了建模范式，以享受自回归模型更好的似然性和灵活长度的生成，以及扩散模型快速和并行的生成。

Block Diffusion 似然

我们提出了一个建模框架，该框架自回归地建模 token 块，并在每个块内执行扩散。我们的似然在 B 个长度为 L′ 的块上分解为 log⁡pθ(x)=∑b=1Blog⁡pθ(xb|x<b) 每个 pθ(xb|x<b) 使用在 L′ 个 token 的块上的离散扩散 ELBO 进行建模。我们通过优化以下似然界限获得有原则的学习目标 LBD(x,θ)： log⁡pθ(x)≥LBD(x,θ):=∑b=1BLdiffusion(xb,x<b,θ), 我们在一个简单的离散扩散参数化下对每个块的似然进行建模 (Sahoo et. al, Shi et. al, Ou et. al)。我们的最终目标变成了加权交叉熵项的总和： LBD(x,θ):=−∑b=1BEt∼[0,1]Eq1tlog⁡pθ(xb|xtb,x<b)

高效的训练和采样算法

通常，我们会通过循环 B 次来应用 xθb(xtb,K1:b-1,V1:b-1) 来计算 logits。相反，我们只需要两次前向传递。第一次传递为完整序列 x 预计算键和值 K1:B,V1:B。在第二次前向传递中，我们使用 xθb(xtb,K1:b-1,V1:b-1) 同时计算所有块的去噪预测。为了从 BD3-LMs 中采样，我们一次生成一个块，并以先前采样的块为条件。生成一个块后，我们缓存它的键和值，类似于 AR。我们可以使用任何扩散采样程序 SAMPLE(xθb,K1:b-1,V1:b-1) 从条件分布 pθ(xsb|xtb,x<b) 中采样，每个块进行 T 个采样步骤。 mask BD3-LM 训练和采样算法。

理解扩散和 AR 模型之间的似然差距

案例研究：单个 Token 生成

在 L′=1 的极限情况下，我们的 Block Diffusion 参数化在期望上等价于自回归 NLL。令人惊讶的是，当在 LM1B 数据集上训练这两个模型时，我们发现 L′=1 的 Block Diffusion 模型和 AR 之间存在两点的困惑度差距。我们认为扩散目标的高训练方差是造成困惑度差距的原因。 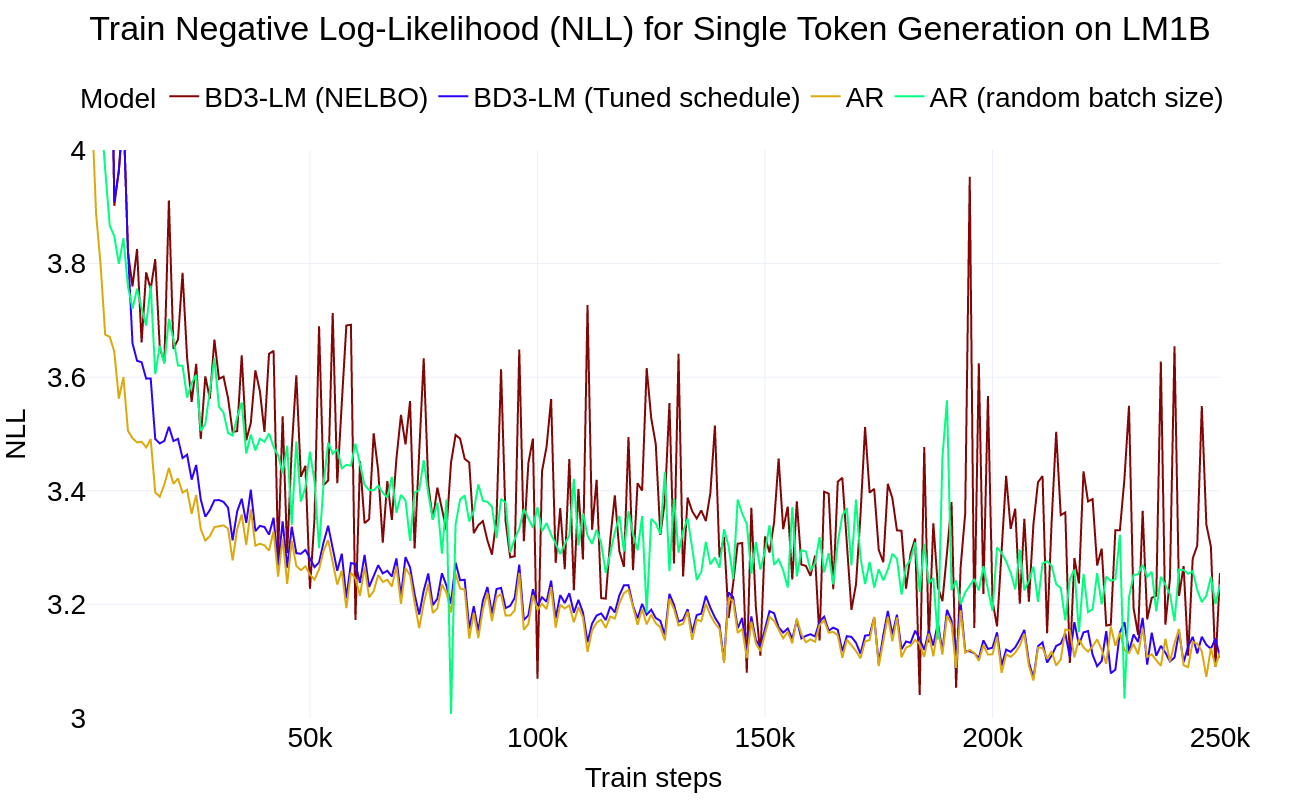mask 在离散扩散 ELBO 下的训练受到高方差的影响。

来自高方差训练的扩散差距

直观地说，如果采样的掩码率 t∼U[0,1] 太低，则重建 x 很容易，这没有提供有用的学习信号。如果我们掩盖了所有内容，那么最佳重建就是数据分布中每个 token 的边缘，这很容易学习，并且同样没有用。我们试图找到能够最大限度地减少由扩散目标引起的训练方差，并进一步减少困惑度差距的噪声调度。

用于低方差训练的数据驱动噪声调度

为了避免导致高方差训练的掩码率，我们在 “裁剪的” 掩码率 t∼U[β,ω] 下训练 BD3-LMs，其中 0≤β,ω≤1。通过减少训练方差，当我们在均匀采样的掩码率下评估时，我们提高了似然性。由于最佳掩码率可能因块大小 L′ 而异，因此我们在训练期间自适应地学习 β,ω。在实践中，我们在每次验证步骤中使用网格搜索来执行此操作，在 5K 梯度更新后，优化 minβ,ωVarX,t[LBD(θ,β,ω;X)]。下面，我们展示了优化每个块大小的噪声调度可以减少损失估计器的方差，并且与替代调度相比，可以获得最佳的困惑度。在 LM1B 上，在不同噪声调度下训练对困惑度 (PPL ↓) 的影响。所有模型都经过 50K 步微调，并在均匀采样的掩码率下进行评估。对于我们裁剪的调度，我们比较了 L′=4,16 的优化裁剪率。 BD3-LMs | 噪声调度 | PPL | Var. ELBO ---|---|---|--- L' = 4 | 线性 t ~ U[0, 1] | 30.18 | 23.45 裁剪 t ~ U[0.45, 0.95] | 29.21 | 6.24 裁剪 t ~ U[0.3, 0.8] | 29.38 | 10.33 对数 | 30.36 | 23.53 L' = 16 | 线性 t ~ U[0, 1] | 31.72 | 7.62 裁剪 t ~ U[0.45, 0.95] | 31.42 | 3.60 裁剪线性 t ~ U[0.3, 0.8] | 31.12 | 3.58 余弦 | 31.41 | 13.00

结果

似然评估

BD3-LMs 在扩散模型中实现了最先进的似然性。如下所示，BD3-LMs 通过调整块长度 L′ 在扩散和自回归似然之间进行插值。 在 OWT 上，针对训练了 262B 个 token 的模型进行的测试困惑度 (PPL; ↓)。 模型 | PPL (↓) ---|--- AR | 17.54 SEDD | ≤ 24.10 MDLM | ≤ 22.98 BD3-LMs L' = 16 | ≤ 22.27 BD3-LMs L' = 8 | ≤ 21.68 BD3-LMs L' = 4 | ≤ 20.73

任意长度序列生成

许多现有扩散语言模型的一个主要缺点是，它们无法生成比训练时选择的输出上下文长度更长的完整文档。例如，OpenWebText 包含最多 131K 个 token 的文档，而离散扩散模型 SEDD (Lou et. al) 仅限于生成 1024 个 token。下面，我们展示了 BD3-LMs 可以通过解码任意数量的块来生成可变长度的文档。 从在 OWT 上训练的模型中采样 500 个文档的生成长度统计信息。 Median # tokens | Max # tokens ---|--- OWT 训练集 | 717 | 131K AR | 4008 | 131K SEDD | 1021 | 1024 BD3-LM L'=16 | 798 | 9982 我们评估了 BD3-LMs 在可变长度序列上的生成质量，使用相同数量的生成步骤 (NFEs) 比较所有方法。下面，我们测量了在 GPT2-Large 下采样的序列的生成困惑度。与所有先前的扩散方法相比，BD3-LMs 实现了最佳的生成困惑度。 300 个可变长度样本的生成困惑度 (Gen. PPL; ↓) 和函数评估次数 (NFEs; ↓)。所有模型都在上下文长度 L = 1024 的 OWT 上训练，并使用 nucleus 采样。 类别 | 模型 | L = 1024 | L = 2048 ---|---|---|--- Gen. PPL (↓) | NFEs | Gen. PPL (↓) | NFEs 自回归 | AR | 14.1 | 1K | 13.2 | 2K 扩散 | SEDD | 52.0 | 1K | - | - MDLM | 46.8 | 1K | 41.3 | 2K Block Diffusion | SSD-LM L' = 25 | 37.2 | 40K | 35.3 | 80K 281.3 | 1K | 261.9 | 2K BD3-LMs L' = 16 | 33.4 | 1K | 31.5 | 2K L' = 8 | 30.4 | 1K | 28.2 | 2K L' = 4 | 25.7 | 1K | 23.6 | 2K 对于 MDLM，我们使用他们的块式解码技术（不包含 BD3-LMs 中的 Block Diffusion 训练）用于 L=2048。我们还与 SSD-LM (Han et. al) 进行了比较，SSD-LM 是一种替代的 Block 自回归方法（也称为半自回归），它在词嵌入上执行高斯扩散，但无法执行似然估计。我们的离散方法使用数量级更少的生成步骤产生具有改进的生成困惑度的样本。

结论

我们提出了 Block Discrete Diffusion 语言模型，这是一种新的模型类，它结合了自回归和扩散方法的优势，同时克服了它们的局限性。Block Diffusion 克服了现有离散扩散模型的关键缺点：与 AR 模型的质量差距以及它们无法生成任意长度的序列或支持 KV 缓存。通过这样做，BD3-LMs 在离散扩散模型中树立了新的标杆。我们的工作在构建功能强大的扩散语言模型方面迈出了有希望的一步，这些模型可以与标准 LLM 相媲美，同时提供并行 token 生成并提高样本的可控性。

BibTeX


    @inproceedings{
     arriola2025interpolating,
     title={Interpolating Autoregressive and Discrete Denoising Diffusion Language Models},
     author={Marianne Arriola and Aaron Gokaslan and Justin T Chiu and Jiaqi Han and Zhihan Yang and Zhixuan Qi and Subham Sekhar Sahoo and Volodymyr Kuleshov},
     booktitle={The Thirteenth International Conference on Learning Representations},
     year={2025},
     url={https://openreview.net/forum?id=tyEyYT267x}
    }