自适应哈希 (Adaptive Hashing)
在2024 ELS上,我做了一个关于自适应哈希的演讲,重点是使通用的哈希表同时 更快且更健壮。
理论与实践
哈希表理论主要关注从哈希函数族中随机选择的哈希函数的渐近最坏情况成本。 尽管这些结果在实践中非常相关,但:
- 那些恼人的常数因子,即大 O 成本忽略的部分,确实很重要,并且
- 我们不会随机选择哈希函数,而是为哈希表的整个生命周期固定哈希函数。
有一些完美哈希算法,可以为给定的键集合选择最佳哈希函数。缺点是它们要么要求键集合是固定的,要么太慢而无法用作通用的哈希表。
尽管如此,通过使哈希函数适应实际键来做得更好,这个想法是关键。我们可以在 在线 做到这一点吗?也就是说,在哈希表被使用时?潜在的性能提升来自于通过以下方式改进上述常数因子:
- 减少冲突,以及
- 提高缓存友好性。
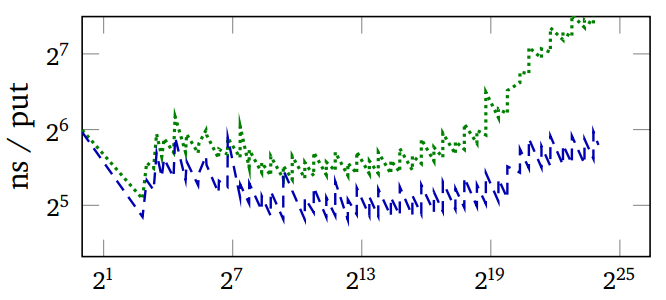
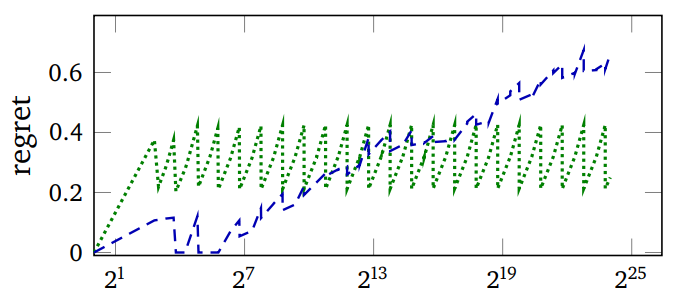
上面的图片绘制了遗憾值(每次查找的预期比较次数减去可实现的最小值)和 PUT 操作的测量运行时间与具有特定键分布的哈希表中的键数量的关系图。绿色是 Murmur(一个健壮的哈希函数),蓝色是 SBCL 快速的 EQ 哈希。图表的摆动是由于将键添加到哈希表时调整了哈希表的大小。
请注意,SBCL 的遗憾值一开始要低得多,但变得比 Murmur 高得多,但如果有的话,它的优势会越来越大。
实现
总体的想法是可靠的,但是由于选择哈希函数和切换到哈希函数的成本,将其转化为真正的性能提升是很困难的。首先,我们必须对键的分布做出一些假设。实际上,语言运行时的默认哈希函数通常会做出这样的假设,以使常见情况更快,通常以削弱最坏情况保证为代价。
本文的其余部分是关于如何修改 SBCL 的内置哈希表(原本已经相当快)的。核心切换机制会关注:
- PUT 操作上的冲突链的长度,
- 重新哈希时的冲突计数(当哈希表增长时),以及
- 哈希表的大小。
适配 EQ 哈希表
- 初始化为常量哈希函数。这是一种花哨的说法,即我们在内部的向量中进行线性搜索。这是一个
EQ哈希表,因此键比较是单个汇编指令。 - 当哈希表增长到超过 32 个键并且必须重新哈希时,我们切换到哈希函数,该函数执行单个右移,其中要移动的位数由键中低位中最长公共运行数确定。
- 如果冲突太多,我们切换到以前的默认 SBCL
EQ-哈希函数,该函数已经调整了很长时间。 - 如果冲突太多,我们切换到 Murmur,这是一个通用的哈希。我们也可以一直使用加密哈希。
在第 2 步中,具有单个移位的哈希函数非常适合内存分配器的行为:对于形成算术序列的键来说,它是一个完美的哈希,对于在循环中分配的相同类型的对象来说,通常是近似正确的。
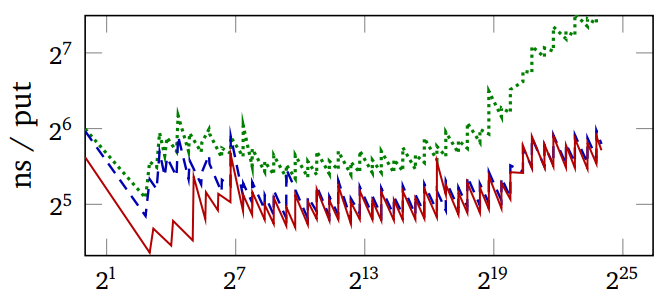 在此图中,红线是自适应哈希。
在此图中,红线是自适应哈希。
适配 EQUAL 哈希表
对于复合键,运行哈希函数是主要的成本。 自适应哈希执行以下操作。
- 对于字符串键,仅哈希前 2 个和后 2 个字符。
- 对于列表键,仅哈希前 4 个元素。
- 如果冲突太多,则将限制加倍。
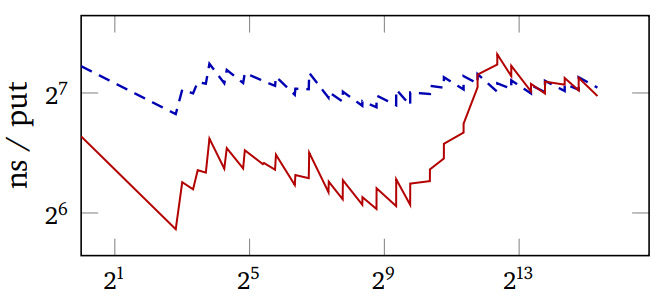
因此,SBCL 哈希表已经自适应了近一年,在常见情况下获得了一些速度,而在其他情况下则获得了健壮性。
完整论文在此。

