如何(真正地)证明它 - **Lean** 中数学与计算的新前沿
如何(真正地)证明它 - Lean 中数学与计算的新前沿
2025年5月8日 lean proof_assistant constructive_mathematics
数学家到底是如何证明的? – 我的意思是,他们坐下来写证明的过程是怎样的?他们如何推测引理?他们决定首先解决哪些问题?以及为什么?
虽然这些问题以前一直是一个谜,但最近的发展,尤其是在机械化数学的最前沿,有望首次揭示这些 行业秘密。
我在这里特别指的是著名数学家(如 Terence Tao, Kevin Buzzard 等)最近对使用 Lean Theorem prover 来形式化真实的、新颖的和前沿的数学成果的兴趣。
当然,数学家们这样做有很多好处1,机器检查过的证明降低了入门门槛,允许前所未有规模的协作,并提供了人类所能提供的最高的正确性保证,但与此同时,这也为非数学家提供了额外的好处:即,一个独特的视角,可以了解数学家的思维方式以及他们实际如何进行证明。
在这篇(有点短的)博文中,我的主要目标是激发人们对最近开启的数学和计算新前沿的兴趣,快速解释这些数据在哪里以及为什么会出现,并且额外的好处是,我们将看到一些有趣的动画(您可以在自己的浏览器中运行!)。
您的浏览器不支持视频标签。 (这是一个为了方便访问的视频,接下来的几个将使用 JavaScript)。
Lean Blueprints
这里的关键要素是这个用于规划 Lean 项目的奇怪的小工具,叫做 Lean Blueprints。
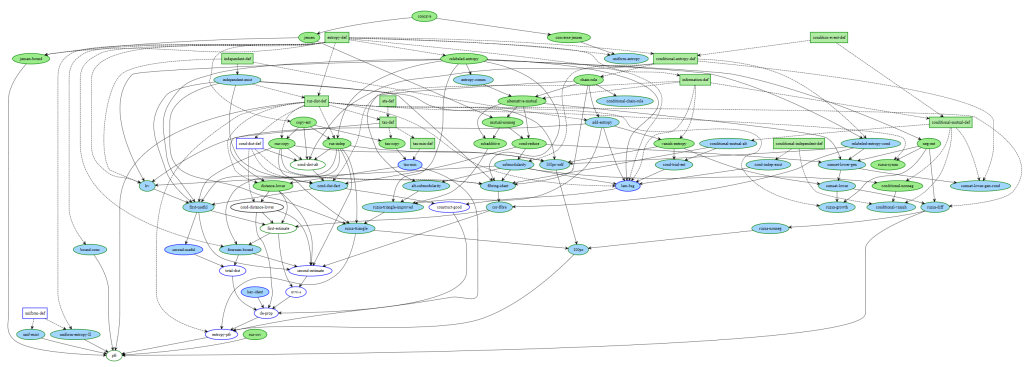
Blueprints 是数学家们为规划其成果的形式化而设计的机制。当将纸笔结果翻译成证明助手时,数学家必须首先编码所有必要的定义、辅助引理等等,然后才能编写证明。 Blueprint 充当跟踪此过程的机制。
上图显示了一个 Blueprint 的示例,取自 Terrence Tao 的 关于 PFR 形式化的博文。它是一个图,其中节点代表形式化中的不同定义、引理和定理。颜色表示形式化的状态。绿色表示已证明;浅蓝色表示可以声明但尚未证明,其余节点(此处为黑色)是甚至无法写下来的节点(它们可能需要先写下一些定义)。
之所以令人兴奋,是因为我们第一次拥有由_数学家_ 为数学家 开发的证明助手的功能,而不是像 Rocq 等证明助手那样由计算机科学家开发。 此外,由于这些形式化是在版本控制中完成的,因此我们实际上可以唯一地访问,以查看 Blueprint 本身在项目形式化过程中如何随时间变化。
例如,如果我们跟踪单个节点,我们可以看到它是如何从甚至没有准备好被声明(黄色)、声明(蓝色)和证明(绿色)的状态转换的:



如果我们查看这些节点周围的图的状态,我们可以访问大量数据,这些数据提供了对数学家如何实际进行证明并构建新工具、技术(也许可以训练一些 ML 模型)以帮助数学家进行证明的独特见解。
为了启动这个过程,我一直在尝试从活跃的 Lean 形式化的版本控制中提取这些数据并尝试绘制出来。
以下是 Terrence Tao 对 Polynomial Freiman Ruzsa 猜想的形式化的 Lean Blueprint 的演变可视化:(GitHub URL:https://github.com/teorth/pfr)
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
如果您播放动画(非常平静),您可以看到数学家们如何随着时间的推移构建 Blueprint 图。 我们可以在看到有趣的东西时随时暂停动画,看看发生了什么。 如果您观看一段时间,您会发现该图通常以黄色的气泡爆发式增长,据推测,某些数学家已经坐下来草绘了证明的另一部分,并将其分解为片段供其他人形式化。 然后,随着形式化的进展,这些节点逐渐被验证,并从蓝色变为最终的绿色。
显然,这并不是一个特别深刻的观察,只是观看了一会儿图的结果,但我确实认为这些数据非常丰富,其中包含许多以前隐藏的关于如何完成这些证明的见解。
用于生成此数据的代码(这篇博文部分是它的广告)可在我的 GitHub 上找到:https://github.com/kiranandcode/lean4-blueprint-extractor/tree/main
探索活跃的 Lean 验证项目
在本博文的其余部分,我将仅为其他一些活跃的 Lean 形式化添加更多可视化效果,并提供一些高级观察。
Roth 数的 Kelley-Meka 边界
GitHub URL: https://github.com/YaelDillies/LeanAPAP
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
此处的时间线可视化提供了一些有趣的见解,说明了 Blueprint 的某些开发是多么的零星。 值得注意的是,时间线仅显示了修改 Blueprint 的提交,因此这里的空白可能对应于数学家主要在 Lean 本身中努力证明东西的地方,而短划线对应于在验证工作上取得实质性进展的地方。
Carleson 定理
GitHub URL: https://github.com/fpvandoorn/carleson
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
该项目说明了数学家们略有不同的开发模式。 似乎开发始于几次“寒武纪”爆发,其中一位研究人员一次性地声明了大量定理。 有趣的是,随着项目的进展,甚至无法声明的黄色定理和定义的数量也在增加,直到后期人们才能在实际证明事情方面取得进展。 顺便说一句,观看图形逐渐将色调变为全绿色非常有趣。
Magmas 的等式理论的关系
GitHub URL: https://github.com/teorth/equational_theories
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
在我们在这篇博文中看到的项目中,这是迄今为止最令人兴奋的。 对于那些不了解该项目的人来说,等式理论形式化工作 在此处提出,对应于 Terrence Tao 及其合作者尝试首先在 Lean 中开发新数学,而不是形式化现有作品。 问题的具体细节可能由数学家更好地解释,但关键是该项目本身为我们提供了一个视角,让我们了解未来的数学可能是什么样子,数学家与机器携手合作,以证明有趣和令人兴奋的新定理。 这在 Blueprint 本身中有所体现,与其他许多 Blueprint 不同,该项目始终具有一组完全绿色的节点,并且随着浅蓝色节点的增加,会缓慢添加新的实验。
解析数论指数数据库
GitHub URL: https://github.com/teorth/expdb/tree/main
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
观看该项目在开始时验证非常不稳定很有趣。 在图中,我们可以看到在开始时,数学家似乎提出了许多定义,并提出了几个他们可以证明的陈述,但是随着项目的发展,这些最初的陈述经历了很多变化——也许它们不适合形式化? — 然后在项目进行到一半时,开发人员又回到了更标准的方法,即首先写下几个非正式的陈述,然后逐步将其形式化。
无穷宇宙理论形式化
GitHub URL: https://github.com/emilyriehl/infinity-cosmos
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
这很有趣,因为它是我认为的某些类别/同伦理论相关数学的形式化,这是数学的一个领域,证明助手在历史上已经取得了一些成功。 Blueprint 的演变看起来与它们在更传统的数学形式化中的演变明显不同。 特别是,开发人员似乎从不一次性声明过多的非正式陈述——我们从未见过以前见过的节点爆炸——并且几个陈述以可以直接形式化的形式写下来。
费马最后定理
GitHub URL: https://github.com/ImperialCollegeLondon/FLT
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
@@ 在我们在这篇文章中看到的项目中,这绝对是最具实验性的,通过查看该图,您真的可以知道这里的作者仍在努力弄清楚如何分解证明:在大部分历史记录中,该图是断开连接的
指数为 3 的费马最后定理
GitHub URL: https://github.com/pitmonticone/FLT3
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
该项目的历史与先前普遍看到的费马最后定理的形式化有些相似。 有趣的是,似乎有很多没有文本的节点被添加? 这可能是我的提取代码中的一个错误,但我认为它对应于首先编写 Lean 代码,并且尚未充实 Blueprint 中的节点的情况。n
球面外翻的存在的形式化
GitHub URL: https://github.com/leanprover-community/sphere-eversion
▶ 加载和播放时间线 正在加载数据... ▶ 播放切换到树状图 放大缩小重置 可声明 未准备好 已证明 可证明 已定义 完全证明
该项目似乎是更多由 Lean 驱动的形式化,没有像数学家拿笔和纸证明并将其脑转储到 Blueprint 中时那样多的非正式陈述的爆发。 形式化似乎首先构建了必要的理论,形成全绿色节点的集群,然后慢慢地将它们连接在一起。 如果我不得不猜测,我会假设计算机科学家项目的 Blueprint 看起来与此非常相似。
脚注
1 诚然,我在这里有点偏颇,因为我的研究工作是在形式化方法领域。

