深入Mipmap选择的细节

Mipmap selection in too much detail

Source | HN Comments

文章探讨了GPU上mipmap层级的选择细节。首先介绍了mipmap的基本概念和作用，解决纹理走样问题。接着，文章解释了像素导数（`ddx()`/`ddy()`）在mipmap选择中的作用，`Texture2D.SampleGrad()` 函数通过偏导数计算mipmap层级。核心在于，文章深入分析了如何通过偏导数计算mipmap层级，并揭示了硬件实现与理论计算的差异，特别是Nvidia硬件的近似处理，以及DirectX 11规范中描述的椭圆变换，用于更精确地计算mipmap级别，以应对非正交的雅可比矩阵情况。

pema.dev About Blog Notes

深入Mipmap选择的细节

2025年5月9日

在这篇文章中，我想阐明我一直疑惑的问题：在GPU上采样纹理时，mipmap层级是如何精确选择的？如果你已经了解什么是mipmap、为什么使用它以及什么是像素导数 (ddx() / ddy())，你可以跳到导数到mipmap层级部分。不过，本文假设读者具备一定的图形编程知识。

Mipmapping入门

在shader中，一个非常常见的操作是纹理采样。在HLSL中，我们通常使用 Texture2D.Sample() 函数来实现。对于一个常规的4通道浮点纹理，完整的函数签名如下所示：

float4 Texture2D.Sample(SamplerState sampler, float2 location);

它接受一个纹理采样位置作为输入，以及一个 SamplerState。SamplerState是一个包含元数据的对象，用于影响采样行为，例如应该使用哪种纹理过滤模式。

下面是一个简单的片段shader的例子，它通过使用第0个UV通道中的纹理坐标对纹理 _Texture 进行采样，从而对每个像素进行着色：

float4 frag (float2 uv : TEXCOORD0) : SV_Target 
{ 
  return _Texture.Sample(sampler_Texture, uv); 
}

当应用到一个四边形并输入一个砖块纹理时，我们得到这样的结果：

请注意，表面看起来有些“像素化”，尤其是在远端边缘附近。这被称为纹理走样。根本原因是屏幕像素所覆盖的纹理空间区域的大小随距离和视角而变化。

举例说明，考虑倾斜的四边形。观察屏幕空间中相同的区域如何对应于纹理空间中非常不同的区域。蓝色正方形大约覆盖 4 个像素，而绿色正方形大约覆盖 12 个，即使它们在屏幕空间中具有相同的面积。

视角越浅，每个屏幕像素覆盖的纹素就越多。由于我们只为每个屏幕像素采样 1 个纹素，因此屏幕像素覆盖的大部分纹素都被走样成单个样本——未被采样的纹素的贡献丢失了！

解决这个问题的典型方法是mipmapping - 我们首先生成一系列更小版本的纹理，称为 mipmaps ，方法是对更高分辨率纹理的纹素进行平均。随着mipmap变得越来越小，它们的内容也变得更加模糊。我们实际上是在对纹理应用一系列低通滤波器。我们通常使用数字来命名mipmap，其中0是全分辨率纹理，随后的每个数字对应于较低分辨率的纹理。我将这些数字称为“mipmap层级”。在由于屏幕像素覆盖了太多的纹素而导致纹理采样会产生走样的情况下，我们会采样一个较低分辨率的mipmap来减轻它。这样，我们就可以获得覆盖区域中纹素的近似平均值。这是之前的相同设置，但现在启用了mipmap：

我根本不需要更改shader来实现这一点 - 当使用 Texture2D.Sample() 并且输入纹理包含mipmap时，GPU会自动为每个样本选择合适的mipmap级别！

如果你像我一样，你不会对这个解释感到非常满意。 GPU 通过 一些魔法 来选择mipmap级别？好的 - 它是如何工作的？这就是本文其余部分的内容。

像素导数

对于片段shader，一个常见的心理模型是“一段代码在一个大的并行for循环中迭代屏幕上的每个像素”。为每个像素并行调用片段shader；每次调用都会获得一组逐像素的输入，并使用它们来计算该像素处的最终颜色。这是一个很好的心理模型，但它并没有说明全部情况。

实际上，片段shader不是针对每个像素孤立地调用的 - 而是针对 2x2 的像素块调用的，通常称为“像素四元组”，或简称为“四元组”。这种设置允许我们使用有限差分方法来近似屏幕空间中任何变量的偏导数！在HLSL中，执行此操作的函数称为 ddx() 和 ddy()，并分别返回沿屏幕空间中X轴和Y轴的偏导数。你无法自己实现这些函数 - 它们是由硬件实现的魔法内部函数。其原理是减去quad中不同像素相关联的值。

现在，观察如果我们应用一个小片段shader来可视化UV坐标的Y轴上的偏导数会发生什么，UV坐标是我们用来采样之前纹理的坐标：

float4 frag (float2 uv : TEXCOORD0) : SV_Target 
{ 
  // 乘以 15 以便我们实际看到导数，
  // 它们通常非常小。
  return float4(ddy(uv), 0, 1) * 15;
}

视角越浅，偏导数就越大。此外，偏导数离相机越远越大。

这些条件与纹理采样会导致难看的走样的情况相符，因此mipmap层级的选择与用于采样纹理的输入坐标的偏导数有关，这不足为奇。实际上，Texture2D.Sample() 可以看作是更通用的 Texture2D.SampleGrad() 函数的语法糖：

// 这 2 行代码是等效的：
Texture2D.Sample(sampler, location);
Texture2D.SampleGrad(sampler, location, ddx(location), ddy(location));

Texture2D.SampleGrad() 显式地获取采样位置的偏导数，而 Texture2D.Sample() 使用 ddx() 和 ddy() 隐式地计算它们。在采样位置以阻止 ddx() 和 ddy() 返回有用的偏导数的方式扭曲的情况下（例如，在纹理光线步进或视差映射期间），显式传递这些偏导数可能很有用。它还允许我们在有办法计算它们的情况下使用解析偏导数。

此描述仍然留下一个未解决的问题：Texture2D.SampleGrad() 如何精确地使用输入偏导数来确定要采样哪个mipmap级别？

导数到mipmap级别

Texture2D.SampleGrad() 具有一些内部逻辑，可以将采样位置的偏导数映射到特定的mipmap级别。但是，此函数直接对应于GPU上的硬件指令，因此我们很遗憾无法“查看代码”。为了更好地了解其工作原理，我们可以问两个问题：映射在概念上是什么样的，以及硬件在实践中做什么？令人惊讶的是，这两个问题都很难在网上找到好的答案，但我将逐一解决它们。

映射在概念上是什么样的？

你可能会想到在图形库的选择规范中查找有关映射应如何工作的信息。我发现GLES3.0规范特别易于阅读。根据第3.8.10.1节“比例因子和细节级别”，mipmap级别的计算方式如下：

MipLevel(x,y)=log2(ρ(x,y))

其中 x,y 是屏幕像素的坐标，而 ρ 是由下式定义的“比例因子”：

ρ=max{(∂u∂x)2+(∂v∂x)2,(∂u∂y)2+(∂v∂y)2}

在此，u 和 v 表示纹理空间中采样位置的坐标，缩放到范围 [0; TextureSize]，因此 ∂u∂x 例如是采样位置水平坐标关于 x 的偏导数，即 ddx(u * textureSize)。

这有点拗口，让我们将其翻译成代码：

float MipLevel(float u, float v, float textureWidth, float textureHeight)
{
  float du_dx = ddx(u * textureWidth);
  float dv_dx = ddx(v * textureHeight);
  float du_dy = ddy(u * textureWidth);
  float dv_dy = ddy(v * textureHeight);
  float lengthX = sqrt(du_dx*du_dx + dv_dx*dv_dx);
  float lengthY = sqrt(du_dy*du_dy + dv_dy*dv_dy);
  float rho = max(lengthX, lengthY);
  return log2(rho);
}

这应该有点直观 - 随着偏导数的大小增加，mipmap级别也应该增加。我们只真正在意走样最严重的轴（幅度最大的轴），因此有 max()。 log2() 解释了mipmap级别中的每次增量对应于采样大小为一半的纹理的事实。

如果你在网上搜索如何手动计算mipmap级别，你可能会找到像这样的解决方案。但是，正如我们很快将看到的，这并不是全部情况。

硬件实际上做了什么？

由于 Texture2D.SampleGrad() 是用硬件实现的，因此我们无法直接查看实现。但是，我们可以使用对其行为的观察来推断它在做什么。为了方便起见，我首先需要一个mipmap，这些mipmap很容易彼此区分。幸运的是，大多数图形框架允许你手动填充每个mipmap的纹理数据 - 它们不必是全分辨率纹理的模糊版本。由于我使用Unity进行可视化，因此我编写了一个小脚本，该脚本生成一个纹理，其中每个mipmap都是单个、明亮、清晰可区分的颜色。结果纹理如下所示：

接下来，我编写了一个shader，该shader使用 Texture2D.SampleGrad() 采样纹理，但采样位置是常量，并且偏导数基于UV坐标。 Texture2D.SampleGrad() 获取采样位置的X轴和Y轴的偏导数，每个偏导数都是二维向量，因此这在技术上是一个六维函数。由于我们保持采样位置固定，因此实际上这是一个四维函数。维度超过 3 的函数很难可视化，因此我现在将只关注 X 轴的偏导数，而将 Y 轴的偏导数保留为 0：

float4 frag (float2 uv : TEXCOORD0) : SV_Target 
{ 
  // 将 UV 从 [0; 1] 缩放到 [-1; 1]
  float2 scaledUV = (uv - 0.5) * 2.0;
  // 在位置 (0.5, 0.5) 处采样纹理，
  // 使用 X 导数 = UV 坐标，
  // 和 Y 导数 = 0。
  float2 samplingLocation = 0.5;
  float2 yDerivative = 0;
  float4 hardwareSample = _MainTex.SampleGrad(
    sampler_MainTex,
    samplingLocation,
    scaledUV.xy,
    yDerivative); 
 
  return hardwareSample;
}

在四边形上应用此shader会在我的机器上产生此结果（GPU是 RTX 4070 Super）：图像经过缩放，使左下角对应于 (-1, -1) 的 X 轴偏导数，右上角对应于 (1, 1)。每个像素的颜色指示在将等于像素坐标的偏导数传递给 Texture2D.SampleGrad() 时采样的mipmap级别。

当我第一次看到这个结果时，我有点惊讶。为什么会有锯齿状边缘？！前面部分中描述的公式应该会产生一堆完美的同心圆！事实证明，当前的图形库将实现的细节留给GPU供应商，并且仅对实现规定了一些宽松的标准。 Nvidia卡使用了一种特别粗糙的近似。

旁注：这只是在不同供应商之间实现的许多功能之一。当人们假设在GPU领域中几乎任何事物都存在“一个真实的正确”实现时，这让我很恼火。举几个其他供应商不同的领域：cos(x) 和 sin(x) 等超越函数的精度、AlphaToCoverage的实现（AMD使用抖动）、光栅化器输出中的细微差异，尤其是在保守光栅化方面等等。不幸的是，当对涉及图形管道的任何内容进行基于图像/黄金图像的测试时，这是一个很大的痛苦来源，并且是此类测试设置通常具有每个平台的参考图像并使用模糊比较的原因之一。

我的下一个本能是确定哪些供应商 实际上 在其实现中有所不同，以及在多大程度上有所不同。我要求一堆朋友在他们的硬件上尝试一下并收集结果。我在这里只渲染具有正偏导数的象限，因为无论如何形状都是对称的：

关于我的发现的一些注意事项：

所有经过测试的供应商似乎都大致同意映射函数。每个图像都类似于一组具有相同半径的同心圆。但是，每个供应商对圆的近似程度差异很大。
没有两个供应商完全同意该实现。
所有经过测试的供应商似乎在其硬件阵容中保持一致。有趣的是，AMD的APU与其专用GPU一致。
结果在Unity支持的所有图形库中都相同（我检查过了）。

有了这个，我提出了可能是有史以来第一个GPU层级列表，该列表按照偏导数到mipmap级别映射函数的保真度进行排名（显然，这是唯一重要的指标）：Adreno/Qualcomm > AMD > Intel > MacBook/Apple > Nvidia。你首先在这里听说，Nvidia硬件很糟糕！（/s）

探索完整的4D映射函数

在先前偏导数到mipmap级别映射函数的可视化中，我仅可视化了X轴偏导数的影响，并将Y轴偏导数保留为（0, 0）。接下来，我想同时可视化两个轴的影响。我发现可视化此四维函数的最简单方法是使用网格。在每个网格单元中，我们将有一个图像，其中 X 轴偏导数发生变化。每个网格单元将对 Y 轴偏导数使用固定值，这些值取决于单元格的位置。这样，我们可以看到完整函数的二维“切片”。我启动了一个Unity脚本来使用之前的shader渲染出来，该脚本生成了此图像：

注意：这种可视化将在整个帖子中多次弹出，因此值得强调我们正在看什么：左下角的网格单元具有恒定的 Y 轴偏导数 (0, 0)，而右上角的网格单元具有恒定的 Y 轴偏导数 (1,1)，它们之间的所有单元格都具有介于 0 和 1 之间的某个位置的恒定 Y 轴偏导数。在每个网格单元中，局部 X 和 Y 坐标决定了 X 轴偏导数。我仅可视化正 Y 轴偏导数，因为负偏导数的图像只是相同的，但已镜像。颜色再次指示选定的mipmap级别。当然，此图像非常特定于供应商 - 这些图像都是在 RTX 4070 Super 上生成的。

使用此设置，我们可以轻松地将硬件所做的事情与映射在概念上是什么样的？部分中提出的软件实现进行比较，方法是使用 Texture2D.SampleLevel() 显式采样我们已选择的mipmap级别。这是相同的图像，但使用软件实现： ![](https://pema.dev/assets/WeirdMips 1.png) 看起来……与硬件实现大不相同。正如预期的那样，软件实现会生成完美的圆形图案，而硬件实现会近似它们。但是，此外，只要 X 轴和 Y 轴 偏导数都具有非零分量，硬件实现就会生成某种椭圆形状，而软件实现仅会生成完美的圆形。当我第一次看到它时，这让我有点惊讶，因为在我的初步研究中，我没有发现任何提及这种行为的信息。这激发了我的兴趣，并促使我尝试对该行为进行逆向工程。答案就在那里，我只需要更深入地挖掘……

对硬件实现进行逆向工程

我设法找到的第一个提及与mipmap级别选择相关的椭圆的资源是DirectX 11.3 功能规范（赞美它），在第 7.18.11 节“LOD计算”中。我将简要地重述规范的相关部分，然后对其进行剖析：

给定一对表示椭圆变换的偏导数向量，重要的是使用Heckbert 89描述的适当正交雅可比矩阵计算LOD。执行各向异性过滤时，也必须使用这些修改后的向量来计算适当的过滤占用空间。 D3D11.3 将允许对此效果进行近似。以下描述了给定二维向量的理想变换：

隐式椭圆系数：
A = dX.v ^ 2 + dY.v ^ 2
B = -2 * (dX.u * dX.v + dY.u * dY.v)
C = dX.u ^ 2 + dY.u ^ 2
F = (dX.u * dY.v - dY.u * dX.v) ^ 2

定义以下变量：

p = A - C
q = A + C
t = sqrt(p ^ 2 + B ^ 2)

然后可以将新向量计算为：

new_dX.u = sqrt(F * (t+p) / ( t * (q+t)))
new_dX.v = sqrt(F * (t-p) / ( t * (q+t)))*sgn(B)
new_dY.u = sqrt(F * (t-p) / ( t * (q-t)))*-sgn(B)
new_dY.v = sqrt(F * (t+p) / ( t * (q-t)))

以下警告也适用：
- 如果 dX 或 dY 的长度为零，则实现应跳过这些变换。
- 如果 dX 和 dY 平行，则实现应跳过这些变换。
- 如果 dX 和 dY 垂直，则实现应跳过这些变换。
- 如果 dX 或 dY 的任何分量为 inf 或 NaN，则实现应跳过这些变换。
- 如果 dX 和 dY 的分量足够大或足够小以导致这些计算中的 NaN，则实现应跳过这些变换。
如果(ComputeIsotropicLOD)，则 LOD 计算为：

float lengthX = sqrt(dX.u*dX.u + dX.v*dX.v + dX.w*dX.w)
float lengthY = sqrt(dY.u*dY.u + dY.v*dY.v + dY.w*dY.w)
output.LOD = log2(max(lengthX,lengthY))

哇，这有点拗口了…… 在规范的片段中，dX 和 dY 表示我们先前讨论过的 X 轴和 Y 轴偏导数。这些向量的 w 分量仅用于 3D 和立方体贴图纹理，因此与此无关。请注意，最后一个片段中的代码几乎与我们之前测试过的软件实现完全一样。但是，该片段之前的大部分文本描述了某种“椭圆”变换，该变换应在计算其长度之前应用于偏导数。这听起来很有希望，因此让我们尝试理解该规范的规定。

缺少椭圆变换

支线任务：纹理过滤理论和向量微积分

在描述椭圆变换之前，我们需要访问纹理过滤理论和向量微积分中的一些思想。如果你已经熟悉雅可比矩阵和像素占用空间的概念，则可以跳到下一节了解椭圆变换。

渲染纹理表面的一个简单方法是：对于每个屏幕像素，确定表面上的对应点，找到其在纹理空间中的对应点，然后读取纹理中最接近该点的值。正如我们之前确定的那样，此方法会导致走样；当屏幕像素覆盖太多的纹素并且仅采样一个纹素时，来自大多数覆盖纹素的贡献会丢失。更好的方法是积分每个屏幕像素覆盖的区域，从所有覆盖的纹素收集贡献。 Mipmapping 是一种使用预计算表近似此积分的廉价方法。

理想情况下，我们希望对屏幕像素在纹理上的投影进行积分。此投影称为像素的“占用空间”。为此，我们想知道屏幕空间中的单位面积（即像素）在投影到纹理空间时如何变换。用于描述空间之间（例如投影）映射导致的面积变化的典型数学工具称为“ 雅可比矩阵”，或简称为“雅可比矩阵”。当用于变换点时，映射的雅可比矩阵提供该点处映射的最佳线性近似。当雅可比矩阵是一个方阵时，其行列式描述了该点处的空间“拉伸”程度。雅可比矩阵由输入空间中坐标相对于输出空间中坐标的一阶偏导数构成。在我们的例子中，输入空间是屏幕空间，输出空间是纹理空间。雅可比矩阵如下所示：

[∂u∂x∂u∂y∂v∂x∂v∂y]

其中 (u,v) 是纹理空间中的坐标，而 (x,y) 是屏幕空间中的坐标。如果你到目前为止都注意到了，这可能会让你想起一些内容 - 这些偏导数可以使用 HLSL 中的 ddx() 和 ddy() 计算。换句话说，我们可以将传递给 Texture2D.SampleGrad() 的偏导数视为形成一个雅可比矩阵，该矩阵描述了渲染纹理表面所涉及的投影映射。

实际上，对屏幕像素的实际占用空间进行积分是不切实际的，因为它通常是一个曲线四边形（具有弯曲边缘的四边形）- 一个非常令人不快的形状。因此，大多数方法都将其近似为常规四边形或椭圆，如下图所示（图片来源）。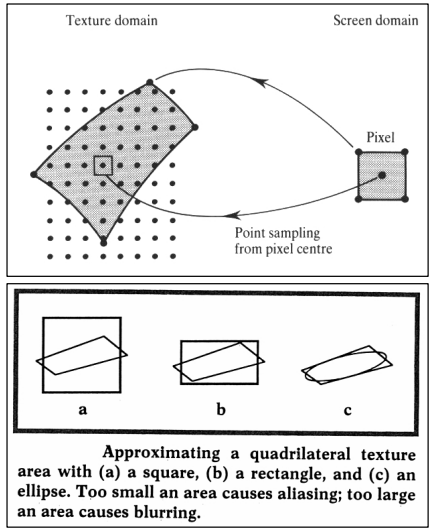

使用 mipmapping 时，我们主要对占用空间的大小感兴趣。面积越大，我们需要使用的mipmap级别就越大，因为较高的mipmap级别对应于对纹理较大区域的积分的近似值。

了解椭圆变换

考虑到这些概念，让我们剖析 DirectX 11 规范中描述的椭圆变换。第一段写道：

“给定一对 表示椭圆变换 的偏导数向量，重要的是使用 Heckbert 89 描述的 适当正交雅可比矩阵 计算 LOD。”

我用粗体文本突出显示了这两个重要概念。我们有纹理采样坐标的偏导数，但是在什么意义上这些表示椭圆变换？想象一下用一个单位圆来表示每个屏幕像素，该单位圆由一个角度 θ 描述，这样 s(θ) 的计算结果为单位圆周长上的所有点：

s(θ)=[cos(θ)sin(θ)]

如果我们另外构造上一节中描述的雅可比矩阵：

[∂u∂x∂u∂y∂v∂x∂v∂y]

... 并通过矩阵乘法使用雅可比矩阵变换单位圆以获得新函数：

p(θ)=[∂u∂x∂u∂y∂v∂x∂v∂y][cos(θ)sin(θ)]

结果函数 p(θ) 将描述 一个椭圆，其中雅可比矩阵的 2 个列向量（即 X 轴和 Y 轴偏导数）位于椭圆的周长上。在列向量垂直且具有相同长度的特殊情况下，结果仍然只是一个（可能缩放的）圆。当列向量垂直但具有不同长度时，结果是一个椭圆，其中列向量是椭圆的长半轴和短半轴。如果向量不垂直，则这不适用。

这解释了该段的第一部分，那么“适当正交雅可比矩阵”部分是什么意思？当雅可比矩阵的列向量不垂直时，雅可比矩阵不构成正交基 - 由雅可比矩阵变换的形状将被剪切。回想一下，选择mipmap级别涉及计算 2 个长度 - 在我们之前的软件实现中，这是通过以下方式完成的：

float lengthX = sqrt(du_dx*du_dx + dv_dx*dv_dx);
float lengthY = sqrt(du_dy*du_dy + dv_dy*dv_dy);

当雅可比矩阵的列向量垂直时，此代码会计算到椭圆周长上最远点的距离，该椭圆的长半轴和短半轴由列向量给出。你可以将此视为沿着最拉伸的轴测量椭圆的“拉伸”程度。这正是我们想要的mipmap - 椭圆占用空间越拉伸，它覆盖的纹素就越多，我们需要的mipmap级别就越高。但是，当列向量不垂直时，剪切会破坏此拉伸度量。我们需要通过在不同的坐标系中计算度量来手动校正此问题。为此，我们需要 对角化 椭圆。

对角化椭圆意味着找到一个坐标系，其中椭圆与轴对齐。特别是，长轴和短轴应与坐标系的 X 轴和 Y 轴对齐。这消除了剪切，并允许我们正确计算拉伸度量。

注意：对于好奇的读者，此“对角化”与矩阵对角化密切相关，该矩阵将矩阵分解为其特征向量和特征值。实际上，椭圆可以表示为一个 2x2 矩阵，其特征向量给出长轴和短轴的方向，而其特征值与轴的长度有关。

DirectX 11 规范的接下来的几段描述了一种用于执行此对角化的算法，该算法取自 Heckbert 89。此算法的细节不是那么重要，因此我不会对其进行描述。相反，为了建立直觉，我已经在图形计算器中实现了该算法，这使我们可以轻松地看到发生了什么：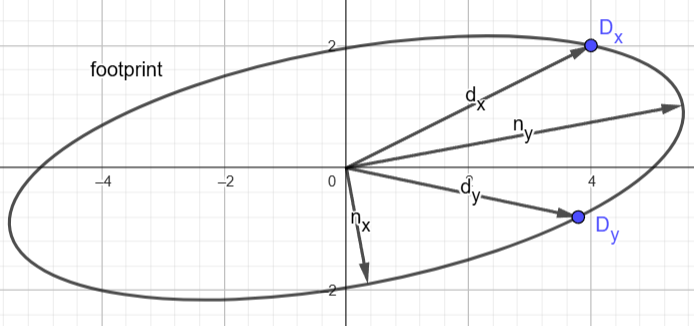

注意：你可以在此处玩此交互式演示。

该图像显示了椭圆占用空间，该椭圆占用空间对应于 X 轴和 Y 轴偏导数（标记为 dx、dy）不垂直的情况。请注意，它们的长度不再描述椭圆的拉伸。该算法的输出（标记为 nx、ny）是一组新的基向量，描述了到坐标空间的变换，在该坐标空间中，椭圆与轴对齐。这些新的基向量是我们“适当正交雅可比矩阵”的列向量。这个新的雅可比矩阵描述的映射几乎与原始映射相同，并且在用于变换单位圆时将产生与原始椭圆完全相同的椭圆。唯一的区别是基向量的指向位置。

此可视化还显示了 DirectX 规范为何提供了一堆应该不应用对角化的角落情况：

以下警告也适用：

如果 dX 或 dY 的长度为零，则实现应跳过这些变换。

如果 dX 和 dY 平行，则实现应跳过这些变换。

如果 dX 和 dY 垂直，则实现应跳过这些变换。

如果 dX 或 dY 的任何分量为 inf 或 NaN，则实现应跳过这些变换。

如果 dX 和 dY 的分量足够大或足够小以导致这些计算中的 NaN，则实现应跳过这些变换。

如果任何一个偏导数为零长度，则坐标将被展平为一条无限线。如果偏导数平行，则会发生同样的情况：如果偏导数垂直，则不存在剪切，因此执行对角化是浪费精力。除此之外，关于 inf 和 NaN 的最后 2 点是不言自明的。

有了椭圆变换，让我们尝试将其添加到我们之前实现的mipmap级别选择的软件实现中：

void EllipseTransformDerivatives(inout float2 dx, inout float2 dy) 
{ 
  bool anyZero = length(dx) == 0 || length(dy) == 0; 
  bool parallel = (dx.x * dy.y - dx.y * dy.x) == 0; 
  bool perpendicular = dot(dx, dy) == 0; 
  bool nonFinite = isinf(dx) || isinf(dy) || isnan(dx) || isnan(dy); 
  if (!anyZero && !parallel && !perpendicular && !nonFinite) 
  {    
    float A = dx.y*dx.y + dy.y*dy.y; 
    float B = -2.0 * (dx.x * dx.y + dy.x * dy.y); 
    float C = dx.x*dx.x + dy.x*dy.x; 
    float F = (dx.x * dy.y - dy.x * dx.y) * (dx.x * dy.y - dy.x * dx.y); 
    float p = A - C; 
    float q = A + C; 
    float t = sqrt(p*p + B*B); 
    float2 newDx, newDy; 
    newDx.x = sqrt(F * (t+p) / ( t * (q+t))); 
    newDx.y = sqrt(F * (t-p) / ( t * (q+t)))*sign(B); 
    newDy.x = sqrt(F * (t-p) / ( t * (q-t)))*-sign(B); 
    newDy.y = sqrt(F * (t+p) / ( t * (q-t))); 
 
    bool failed = any(isnan(newDx) ||