连续思维机器 (Continuous Thought Machines)
此页面需要 JavaScript。请启用它以查看网站。
连续思维机器 (Continuous Thought Machines)
tl;dr 大脑中的神经元在计算时使用时间和同步。 这种属性对于生物智能的灵活性和适应性至关重要。 现代 AI 系统为了效率和简单性而放弃了这一基本属性。 我们找到了一种弥合现代 AI 现有强大实现和可扩展性与 神经元时序至关重要 的生物合理性范例之间差距的方法。 结果令人惊讶和鼓舞。 Luke Darlow Sakana AI Ciaran Regan Sakana AI, University of Tsukuba Sebastian Risi Sakana AI, IT University of Copenhagen Jeffrey Seely Sakana AI Llion Jones Sakana AI MAY 2025 PDF Github
交互演示
❌ 错误加载模型：未找到可用的后端。 错误：[wasm] TypeError: Failed to fetch dynamically imported module: https://cdn.jsdelivr.net/npm/onnxruntime-web/dist/ort-wasm-simd-threaded.jsep.mjs
运行 Teleport 新移动：🟥
仅有效路径
自动求解
显示路径
显示注意力覆盖
动画 FPS：60
点击移动开始/结束（用 ‘move’ 切换）
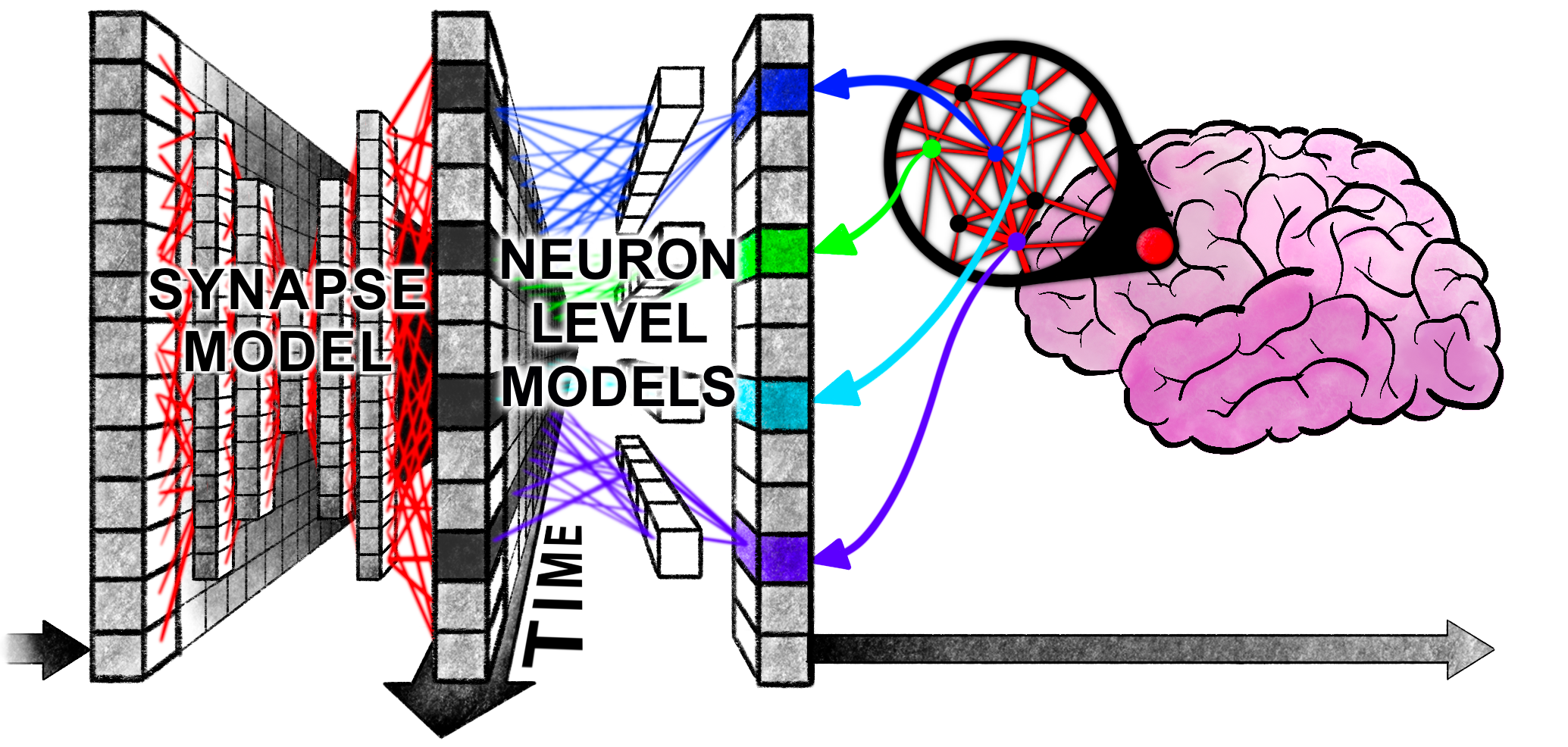这是 Continuous Thought Machine (CTM)：一种新型神经网络，它使用神经活动随时间的同步作为其在世界中采取行动的表示。
这个迷宫求解演示在你的浏览器中运行一个真正的 CTM。 点击运行按钮观看它解决迷宫。 你可以通过点击不同的迷宫位置来移动开始或结束位置。 切换移动按钮可以在移动开始或结束位置之间切换。 Teleport 按钮将起点移动到 CTM 预测的目标 — 团队合作以遍历更长的路径！
当它关注迷宫（显示在迷宫下方并以明亮的方式叠加）时，它会展开 Neural Dynamics：神经活动复杂且随时间变化的模式。 神经元同步的方式是 CTM 与世界交互的方式。 观察它是如何在思考时建立路线的。 玩得开心，尝试用 CTM 快速解决这些迷宫！
请注意，这是一个比我们为 完整结果 训练的模型小得多的模型，并且它可能并不总是像这些结果显示的那样始终如一地表现良好。
介绍
神经网络 (NNs) 最初受到生物大脑的启发，但它们仍然与生物对应物显着不同。 大脑表现出随时间演变的复杂神经动力学，但现代 NNs 有意抽象掉这种时间动力学，以便于大规模深度学习。 例如，标准 NNs 的激活函数可以看作是对神经元放电率的有意抽象，用单个静态值代替了生物过程的时间动力学。 尽管这种简化使大规模机器学习取得了重大进展 [1, 2, 3]，但它导致了与控制生物神经计算的基本原则的背离。 经过数亿年的进化，生物大脑拥有丰富的神经动力学，包括尖峰时序依赖可塑性 (STDP) [4] 和神经元振荡。 模拟这些机制，特别是尖峰时序和同步中固有的时间编码，提出了一个重大挑战。 因此，现代神经网络不依赖时间动力学来执行计算，而是优先考虑简单性和计算效率。 这种抽象虽然提高了特定任务的性能，但导致了人类认知的灵活、通用性质与当前 AI 能力之间的公认差距，这表明我们当前的模型中缺少基本组件，可能与时间处理有关 [5, 6, 7]。
为什么要进行这项研究？
事实上，现代 AI 在许多领域中表现出的显着高性能表明，模拟神经动力学是不必要的。 然而，人类认知的高度灵活和通用性与现代 AI 的当前状态之间的差距表明，我们的当前模型中缺少组件。 出于这些原因，我们认为时间应该是人工智能的核心组成部分，以便它最终达到与或超过人类大脑的水平 [8, 9]。 因此，在这项工作中，我们解决了由于忽视神经活动作为智能的核心方面而施加的强烈限制。 我们引入了 Continuous Thought Machine (CTM)，这是一种新型神经网络架构，旨在明确地将神经时序作为基本要素纳入其中。 我们的贡献如下：
- 我们引入了一个 解耦的内部维度，这是一种对神经活动的时间演变进行建模的新方法。 我们将这个维度视为思想可以在人工神经系统中展开的维度，因此选择了这个命名法。
- 我们为神经元提供了一个中层抽象，我们称之为 神经元级模型 (NLMs)，其中每个神经元都有自己的内部权重，用于处理传入信号（即，预激活）的历史以激活（而不是静态 ReLU，例如）。
- 我们直接使用 神经同步 作为 CTM 观察（例如，通过注意力查询）和预测（例如，通过投影到 logits）的潜在表示。 这种受生物学启发的的设计选择将神经活动作为 CTM 可能展示的任何智能表现的关键要素。
推理模型和递归
人工智能的前沿面临着一个关键时刻：超越简单的输入-输出映射，走向真正的推理能力。 虽然扩展现有模型已经取得了显着的进步，但相关的计算成本和数据需求是不可持续的，并引发了对这种方法长期可行性的质疑。 对于序列数据，长期存在的循环架构 [10, 11, 12] 在很大程度上已被基于 transformer 的方法 [13] 取代。 尽管如此，递归正在重新出现，成为扩展模型复杂性的自然途径。 递归很有希望，因为它能够实现迭代处理和随时间的推移积累信息。 现代文本生成模型（有时称为“推理模型”）使用中间生成作为一种递归形式，从而在测试时实现额外的计算。 最近，其他工作也证明了潜在层的循环应用的好处 [14, 15, 16]。 虽然这些方法使我们更接近于生物大脑的循环结构，但仍然存在一个根本的差距。 我们认为，递归虽然至关重要，但只是难题的一部分。 递归解锁的时间动力学 — 神经活动的精确时序和相互作用 — 同样至关重要。 CTM 与现有方法有三个不同之处： (1) 解耦的内部维度使任何可想象的数据模式都可以进行顺序思考； (2) 私有神经元级模型能够考虑精确的神经时序； (3) 神经同步直接用作解决任务的表示。
方法
图 1. Continuous Thought Machine：其内部循环过程中的一个步骤。 CTM 在思考数据时会在内部展开神经活动。 在每个步骤（上面演示了其中一个步骤）中，都会收集“预激活”的截断历史记录，并将其用于 Neuron Level Models (NLMs)。 随着时间的推移，由所有 NLMs 产生的“后激活”的历史被保留并用于计算神经元到神经元随时间的同步。 结果是 Synchronization Representation：一种新的、参数高效且 显然功能强大 的表示，CTM 使用它来观察（通过注意力）和预测。
Continuous Thought Machine (CTM) 是一种神经网络架构，它能够以一种新颖的方式思考数据。 它通过明确地将 Neural Dynamics 的概念作为其功能的核心组件，从而背离了传统的正向馈送模型。 上面的视频概述了 CTM 的内部工作原理。 我们在我们的 技术报告 中提供了所有技术细节，包括其他图表和详细的解释。 还有一个 GitHub 存储库 可用。 当我们解释下面的模型时，我们将提供指向存储库相关部分的链接。
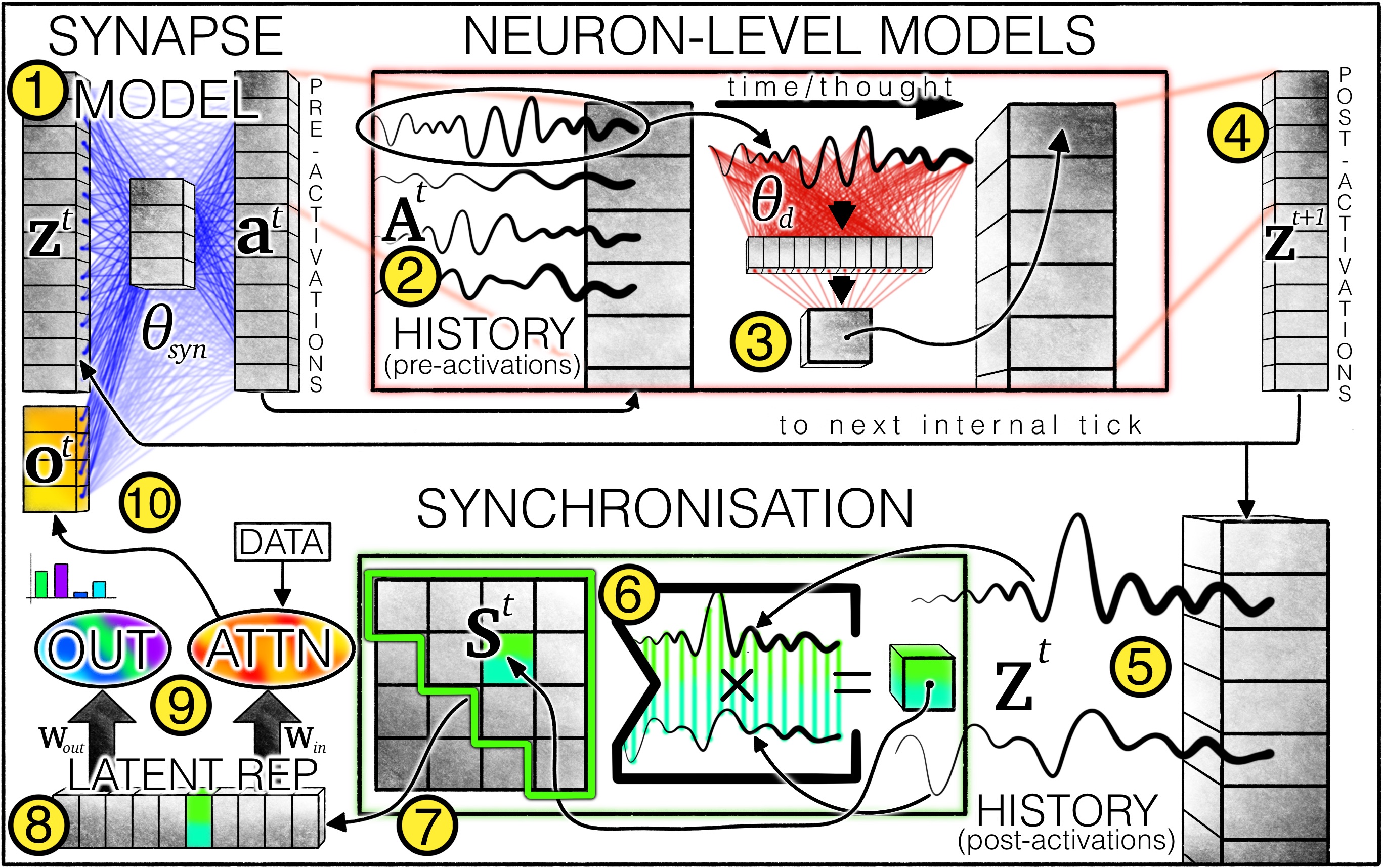图 2. CTM 架构：1 个突触模型（权重表示为蓝线）对跨神经元交互进行建模以产生预激活。 对于每个神经元，保留一个 2 个预激活的历史记录，其中最近的预激活由 3 个神经元级模型（权重表示为红线）使用以产生 4 个后激活。 还保留了 5 个后激活的历史记录，并用于 6 计算同步矩阵。 从同步矩阵中选择 7 个神经元对，产生 8 个潜在表示，CTM 使用它们 9 产生输出并通过交叉注意力调制数据。 调制后的数据（例如，注意力输出）10 与后激活连接以进行下一个内部时钟。 变量 | 说明
---|---
zt | 内部时钟 t 时的后激活，在使用神经元级模型之后。
θsyn | 循环（突触）模型权重； 类似于 U-NET 的架构，它在给定的内部时钟 t 连接神经元。
at | 内部时钟 t 时的预激活。
At | 最近的 预激活的历史记录，设计为 FIFO 列表，因此它们的长度始终为 M； 神经元级模型的输入。
θd | 单个神经元级模型 d of D 的权重； MLP 架构，每个神经元唯一的权重。
Zt | 直到此内部时钟的 所有 后激活的历史记录，可变长度； 用作同步点积的输入。
St | 内部时钟 t 时的同步矩阵。 实际上，对于单独的 Soutt 和 Sactiont 同步表示，我们使用的神经元远少于 D。
Wout, Win | 从 Soutt 和 Sactiont 分别投影到注意力查询和预测的线性权重矩阵。
ot | 交叉注意力输出。
CTM 由三个主要思想组成：
- 使用 内部递归，从而实现了一个维度，在这个维度上可以发生类似于 思想 的概念。 上面的视频中可视化的整个过程是一个时钟； 页面顶部的 交互式迷宫演示 使用 75 个时钟。 这种递归与任何数据维度完全解耦。
- 神经元级模型，它通过将私有（即，在每个神经元的基础上）MLP 模型应用于 传入预激活的历史 来计算后激活。
- 同步作为一种表示，其中跟踪神经活动随时间的推移，并用于计算神经元对如何随时间彼此同步。 这种同步度量是 CTM 采取行动和做出预测的表示。 技术报告 中的列表 3 显示了它的逻辑，附录 K 详细介绍了我们如何使用递归计算来提高效率。
但是数据呢？
虽然数据对于任何建模无疑都是至关重要的，但 CTM 是围绕内部递归和同步的思想设计的，其中数据的作用在某种程度上次于内部过程本身。 输入数据在每个内部时钟上都被注意 并根据当前的同步来摄取，对于预测也是如此。 图 3. 思考 ImageNet 时的神经动力学：每个子图都是单个神经元随时间的活动。 正是这些之间的同步构成了 CTM 使用的表示。
内部时钟：“思考”维度
我们首先介绍连续内部维度：t∈{1,…,T}t \in \{ 1, \ldots ,T \}t∈{1,…,T}。 与传统的顺序模型（例如 RNN 或 Transformers）不同，后者根据数据中固有的序列（例如，句子中的单词或视频中的帧）逐步处理输入，CTM 沿着内部 思考步骤 的自我生成时间线运行。 即使在处理静态或非序列数据（例如图像或迷宫）时，这种内部展开也允许模型迭代地构建和改进其表示。 为了与相关作品中使用的现有命名法保持一致 [17, 18, 19, 20]，我们从现在开始将这些思考步骤称为“内部时钟”。
思想可以展开的维度。
CTM 的内部维度是神经活动动力学可以展开的维度。 我们认为这种动力学可能是智能思想的基石。
循环权重：突触
循环多层感知器（以 U-NET 方式构建的 MLP [21]）充当 CTM 的突触模型。 在任何内部时钟 ttt 时，突触模型都会产生我们认为的 预激活： at=fθ s y n( c o n c a t(zt,ot))∈RD,\bold{a}^t = f_{\theta_{\text{syn}}}(\text{concat}(\bold{z}^t, \bold{o}^t)) \in~\mathbb{R}^D,at=fθsyn(concat(zt,ot))∈RD, 其中 ot\bold{o}^tot 是 来自输入数据。 然后将 MMM 最近的预激活 收集到预激活“历史”中： At=[at−M+1at−M+2⋯at]∈RD×M.\bold{A}^t = \begin{bmatrix}\bold{a}^{t-M+1} & \bold{a}^{t-M+2} & \cdots & \bold{a}^t\end{bmatrix} \in~\mathbb{R}^{D \times M}.At=[at−M+1at−M+2⋯at]∈RD×M.
神经元级模型
MMM 有效地定义了每个神经元级别模型使用的 预激活历史记录 的长度。 然后，每个神经元 {1,…,D}\{1, \ldots, D\}{1,…,D} 都会 获得其自己的私有参数化 MLP，从而产生我们认为的 后激活： zdt+1=gθd(Adt),\bold{z}d^{t+1} = g{\theta_d}(\bold{A}_d^t),zdt+1=gθd(Adt), 其中 θd\theta_dθd 是神经元 ddd 的唯一参数，并且 zdt+1\bold{z}d^{t+1}zdt+1 是包含所有 后激活 的向量中的单个单元。 Adt\bold{A}d^tAdt 是 MMM 维向量（时间序列）。 然后将完整的神经元后激活集合与 注意力输出 连接，并循环馈送到 fθ s y nf{\theta{\text{syn}}}fθsyn 中以产生下一步骤 t+1t+1t+1 的预激活，以用于展开的思考过程。
同步作为一种表示：调制数据
CTM 应该如何与外界互动？ 具体来说，CTM 应该如何消耗输入和产生输出？ 我们引入了一个时间维度，在此维度上可以展开类似于思想的内容。 我们还希望 CTM 与数据的关系（也就是说，它的交互）不依赖于神经元状态的 快照（在某个 ttt 处），而是依赖于 神经元活动持续的时间动态。 通过解决方案，我们再次从自然大脑中寻找灵感，并发现神经同步 [22] 的概念既合适又强大。 对于同步，我们首先将后激活收集到后激活“历史记录”中： Zt=[z1z2⋯zt]∈RD×t.\bold{Z}^t = \begin{bmatrix}\bold{z}^{1} & \bold{z}^{2} & \cdots & \bold{z}^t\end{bmatrix} \in \mathbb{R}^{D \times t}.Zt=[z1z2⋯zt]∈RD×t. Zt\bold{Z}^tZt 的长度等于当前的内部时钟，这意味着 这个维度不是固定的 并且可以是任意大的。 我们将神经同步定义为后激活历史记录之间的内部点积产生的矩阵： St=Zt⋅(Zt)⊺∈RD×D.\bold{S}^t = \bold{Z}^t \cdot (\bold{Z}^t)^\intercal \in~\mathbb{R}^{D\times D}.St=Zt⋅(Zt)⊺∈RD×D. 由于此矩阵以 O(D2)O(D^2)O(D2) 缩放，因此对 (i,j)(i,j)(i,j) 行列对进行子采样是有实际意义的，这捕获了神经元 iii 和 jjj 之间的同步。 为此，我们从 S\bold{S}S 中随机选择 D o u tD_\text{out}Dout 和 D a c t i o nD_\text{action}Daction (i,j)(i,j)(i,j) 对，从而收集两个 同步表示，S o u tt∈RD o u t\bold{S}^t_\text{out} \in~\mathbb{R}^{D_\text{out}}Soutt∈RDout 和 S a c t i o nt∈RD a c t i o n\bold{S}^t_\text{action} \in~\mathbb{R}^{D_\text{action}}Sactiont∈RDaction。 然后可以将 S o u tt\bold{S}^t_\text{out}Soutt 投影到输出空间，如下所示： yt=W o u t⋅S o u tt.\bold{y}^t = \bold{W}{\text{out}} \cdot \bold{S}^t\text{out}.yt=Wout⋅Soutt.
同步启用了一个非常大的表示。
随着模型宽度 D 的增长，同步表示以 D×(D+1)2 增长，从而提供了改进表达能力的机会，而无需更多的参数来将潜在空间投影到此大小。
调制输入数据
S a c t i o nt\bold{S}^t_\text{action}Sactiont 可用于在世界中采取行动（例如，通过注意力，如我们的设置中所示）： qt=W i n⋅S a c t i o nt\bold{q}^t = \bold{W}{\text{in}} \cdot \bold{S}^t\text{action}qt=Win⋅Sactiont 其中 W o u t\bold{W}{\text{out}}Wout 和 W i n\bold{W}{\text{in}}Win 是学习的权重矩阵，用于将同步投影到用于观察（例如，注意力查询，qt\bold{q}^tqt）或输出（例如，logits，yt\bold{y}^tyt）的向量中。 即使在 St\bold{S}^tSt 中有 (D×(D+1))/2(D \times (D+1))/2(D×(D+1))/2 个唯一的配对，D o u tD_\text{out}Dout 和 D a c t i o nD_\text{action}Daction 也可能比这小几个数量级。 也就是说，完整的同步矩阵是一个很大的表示，具有很高的未来潜力。 在我们的大多数实验中，我们使用了标准交叉注意力 [13]： ot= A t t e n t i o n(Q=qt,KV= F e a t u r e E x t r a c t o r( d a t a))\bold{o}^t = \text{Attention}(Q=\bold{q}^t, KV=\text{FeatureExtractor}(\text{data}))ot=Attention(Q=qt,KV=FeatureExtractor(data)) 其中首先使用“FeatureExtractor”模型（例如，ResNet [23]）为键和值构建有用的局部特征。 ot\bold{o}^{t}ot 与 zt+1\bold{z}^{t+1}zt+1 连接，用于下一个递归周期。
损失函数：跨内部时钟优化
CTM 在每个内部时钟 ttt 产生输出。 一个关键问题出现了：我们如何跨此内部时间维度优化模型？ 令 yt∈RC\bold{y}^t \in \mathbb{R}^{C}yt∈RC 为内部时钟 ttt 处的预测向量（例如，类别的概率），其中 CCC 是类别的数量。 令 ytruey_{true}ytrue 为地面真实目标。 我们可以使用标准损失函数（例如交叉熵）在每个内部时钟计算损失： Lt= C r o s s E n t r o p y(yt,ytrue), \mathcal{L}^t = \text{CrossEntropy}(\bold{y}^t, y_{true}),Lt=CrossEntropy(yt,ytrue), 以及相应的确定性度量 Ct\mathcal{C}^tCt。 我们将确定性简单地计算为 1 - 归一化熵。 我们计算所有 t∈{1,…,T}t \in \{1, \ldots, T\}t∈{1,…,T} 的 Lt\mathcal{L}^tLt 和 Ct\mathcal{C}^tCt，从而产生每个内部时钟的损失和确定性，L∈RT\mathcal{L} \in \mathbb{R}^{T}L∈RT 和 C∈RT\mathcal{C} \in \mathbb{R}^{T}C∈RT。 一个自然的问题出现了：我们应该如何将 L\mathcal{L}L 简化为用于学习的标量损失？ 我们的损失函数旨在优化 CTM 在内部思考维度上的性能。 我们不依赖单个步骤（例如，最后一步），这会激励模型仅在该特定步骤输出，而是动态地聚合来自两个内部时钟的信息：最小损失点和最大确定性点：
- 最小损失点：t1= a r g m i n(L)t_1=\text{argmin}(\mathcal{L})t1=argmin(L)；和
- 最大确定性点：t2= a r g m a x(C)t_2=\text{argmax}({\mathcal{C}})t2=argmax(C)。
这种方法是有利的，因为它意味着 CTM 可以在多个内部时钟执行有意义的计算，自然地促进了课程效果，并使 CTM 能够根据问题的难度定制计算。 最终损失计算为： L=Lt1+Lt22. L = \frac{\mathcal{L}^{t_1} + \mathcal{L}^{t_2}}{2}.L=2Lt1+Lt2.
更多信息请参见我们的技术报告。
请查看我们的 技术报告 以获取更多信息。 具体来说，它包括有关我们如何使 CTM 能够学习短期与长期时间依赖关系的其他信息。
实验：ImageNet
演示
启用 JavaScript。 视频播放器正在加载。 播放视频 播放跳过向后跳过向前 静音 当前时间 0:00 / 持续时间 -:- 已加载：0.00% 0:00 直播类型 直播 寻找直播，当前落后于直播直播 剩余时间 --:- 1x 播放速度
- 3x
- 2x
- 1.5x
- 1x，已选择
- 0.5x
- 0.1x
章节
- 章节
描述
- 描述已关闭，已选择
字幕
- 字幕设置，打开字幕设置对话框
- 字幕已关闭，已选择
音轨
画中画全屏
这是一个模式窗口。
无法加载媒体，原因是服务器或网络故障，或者不支持格式。
对话窗口开始。 按 Esc 将取消并关闭窗口。
文本颜色白色黑色红色绿色蓝色黄色洋红色青色不透明度不透明半透明文本背景颜色黑色白色红色绿色蓝色黄色洋红色青色不透明度不透明半透明透明字幕区域背景颜色黑色白色红色绿色蓝色黄色洋红色青色不透明度透明半透明不透明
字体大小 50% 75% 100% 125% 150% 175% 200% 300% 400% 文本边缘样式无凸起凹陷统一阴影字体系列比例无衬线字体等宽无衬线字体比例衬线字体等宽衬线字体休闲字体小大写字母
重置将所有设置恢复为默认值完成
关闭模式对话框
对话窗口结束。
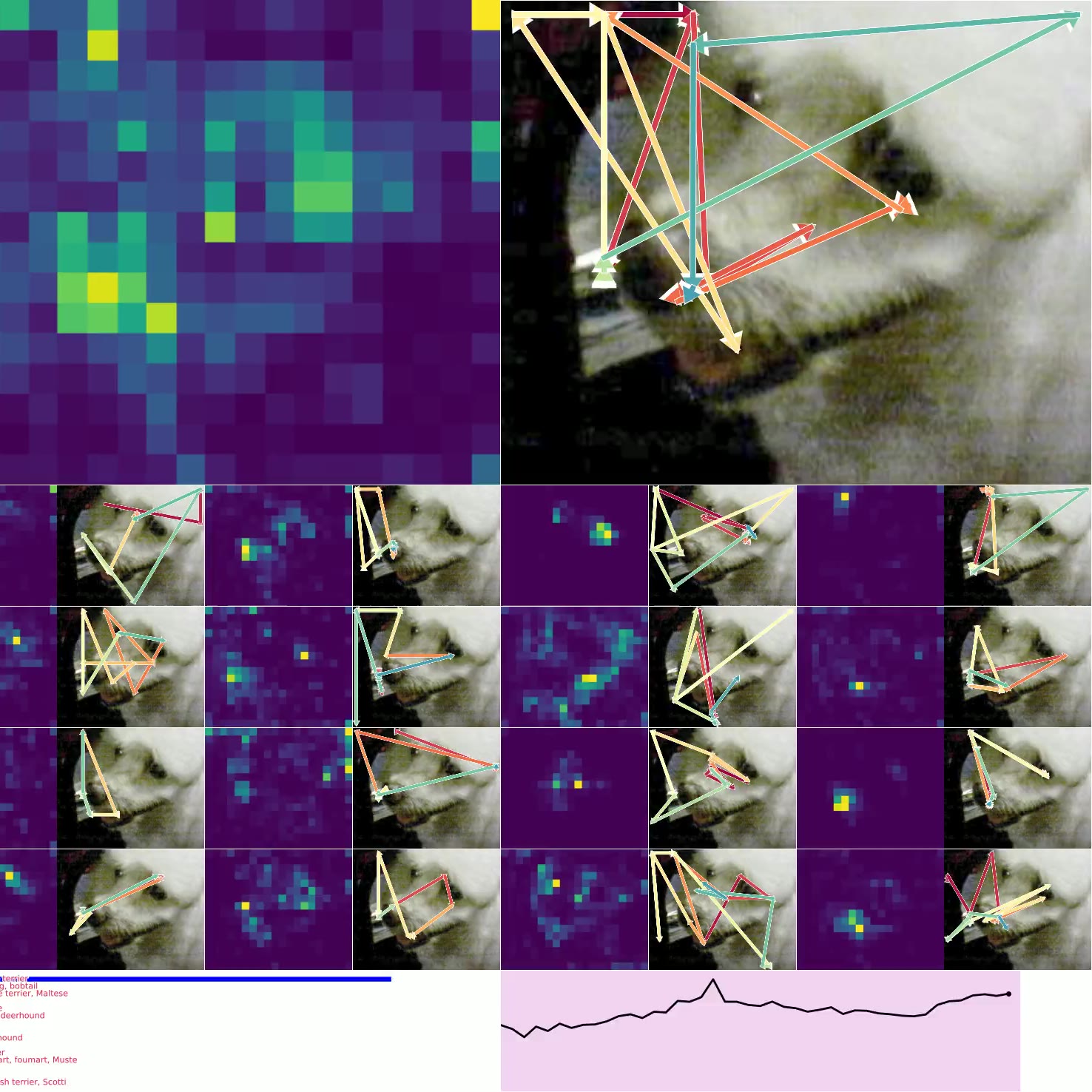
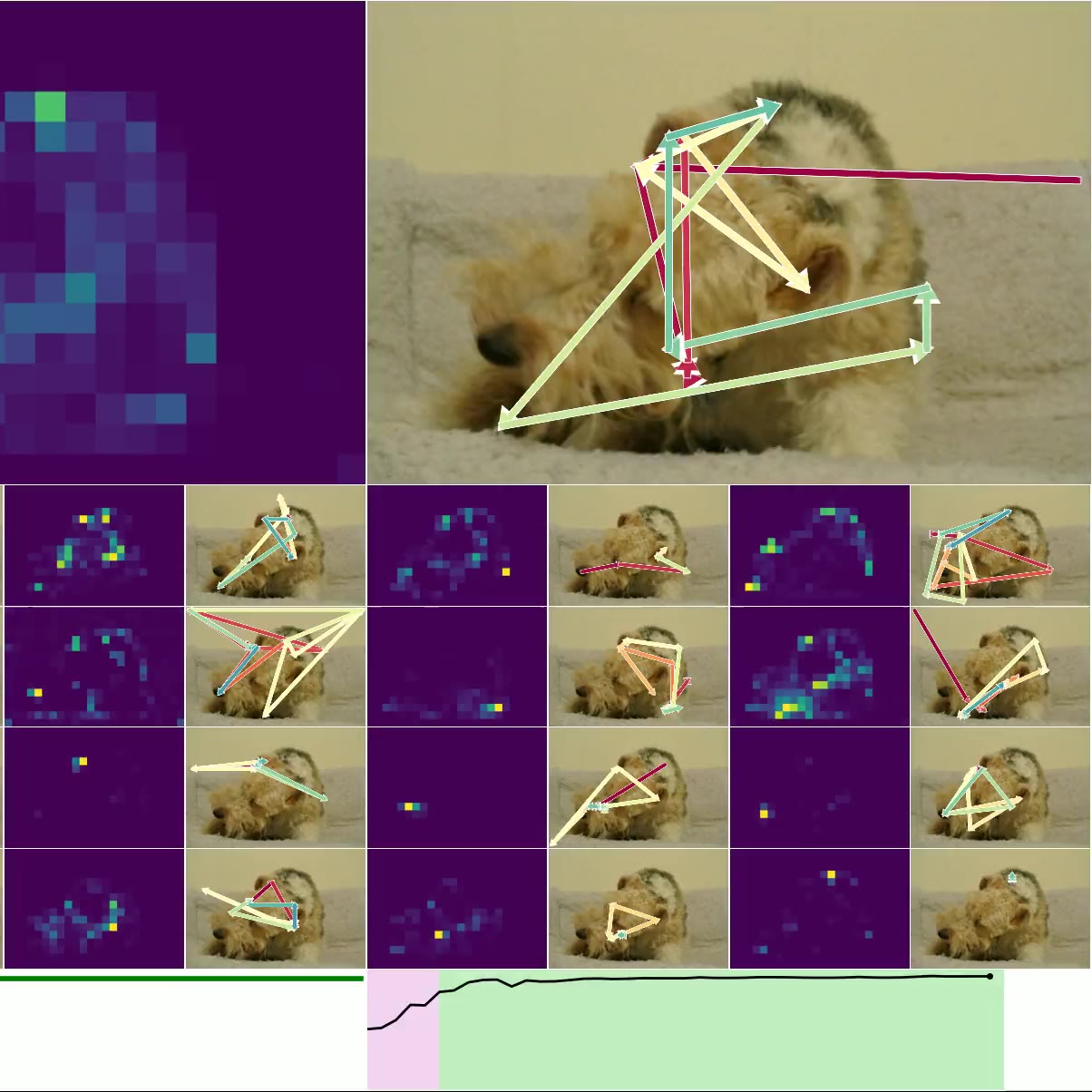
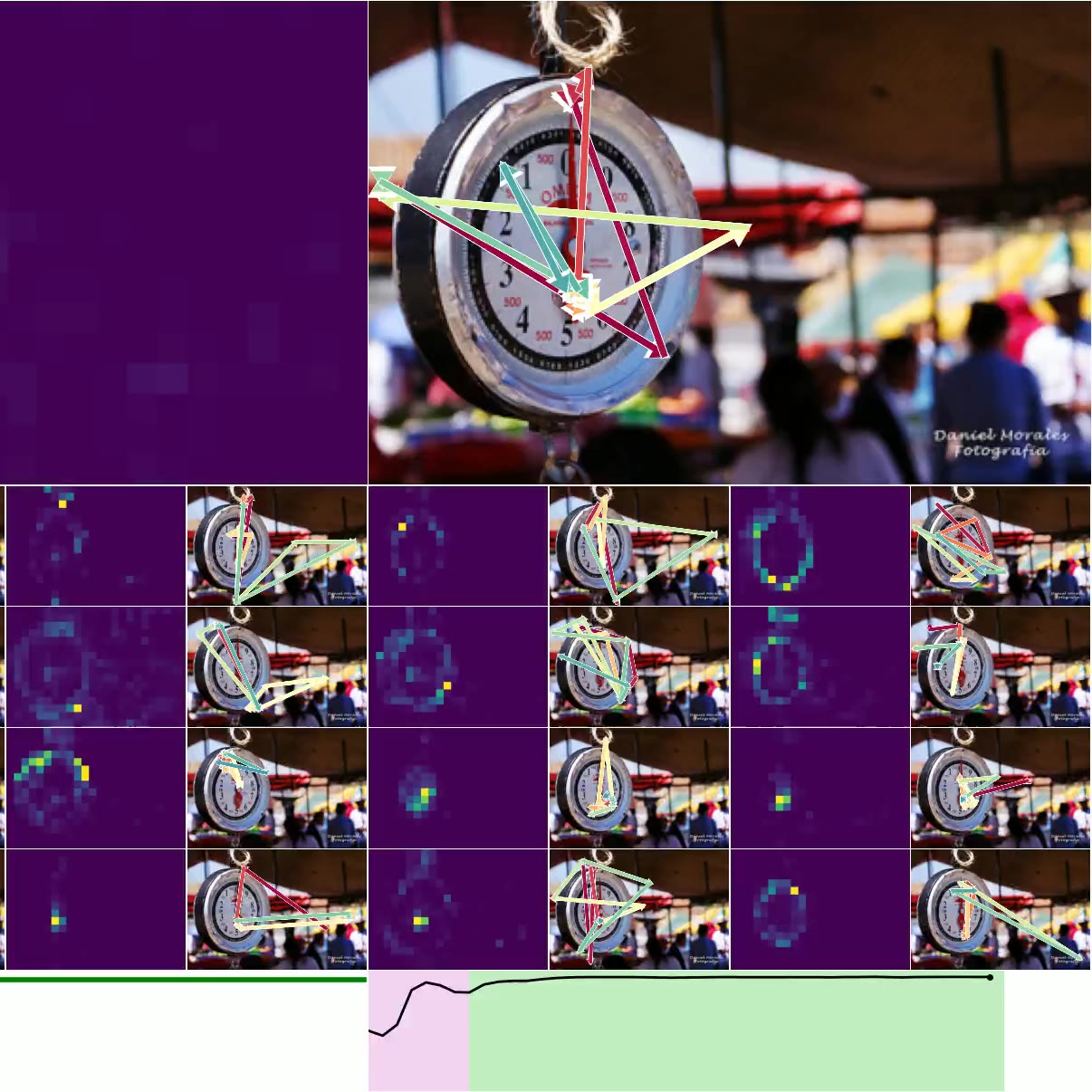
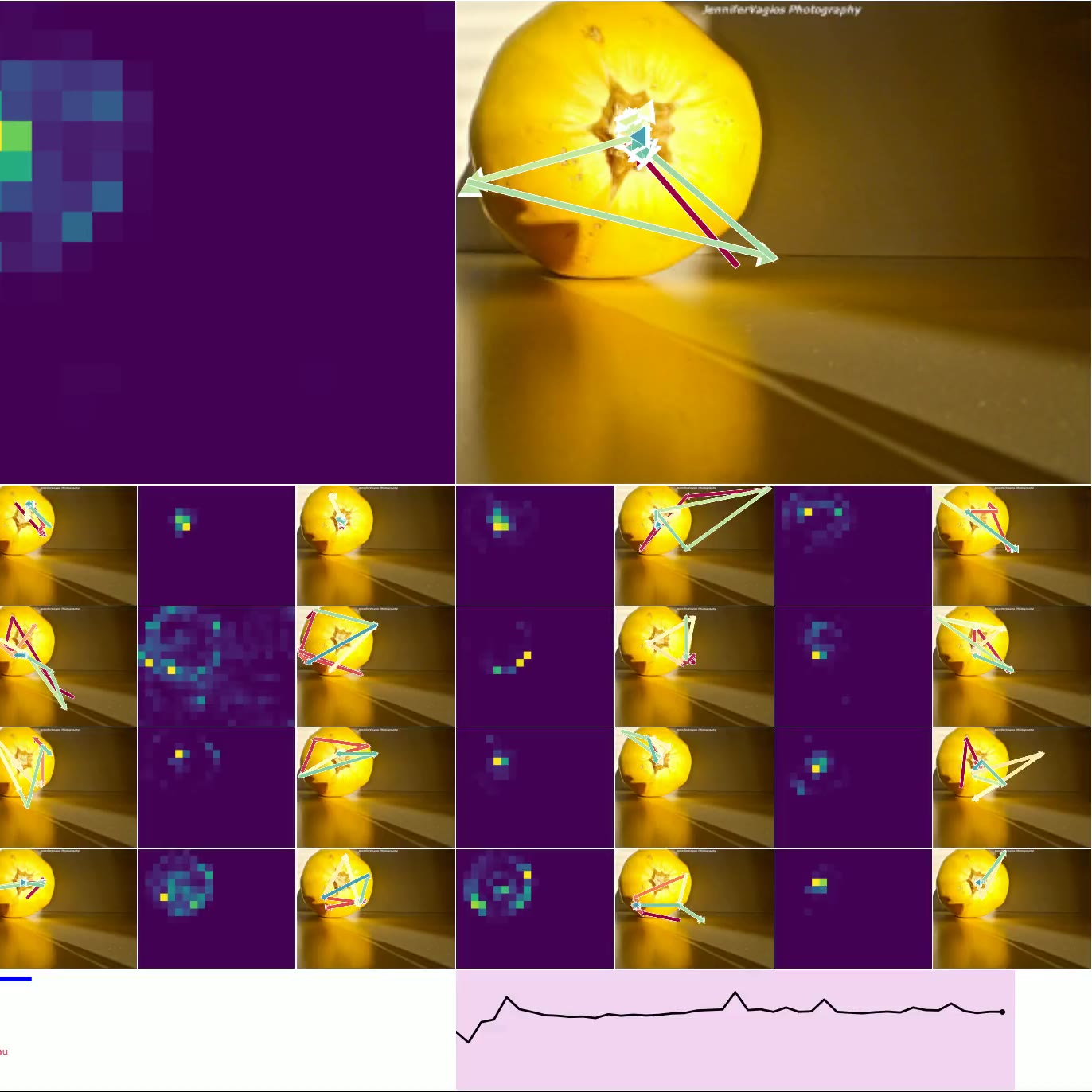
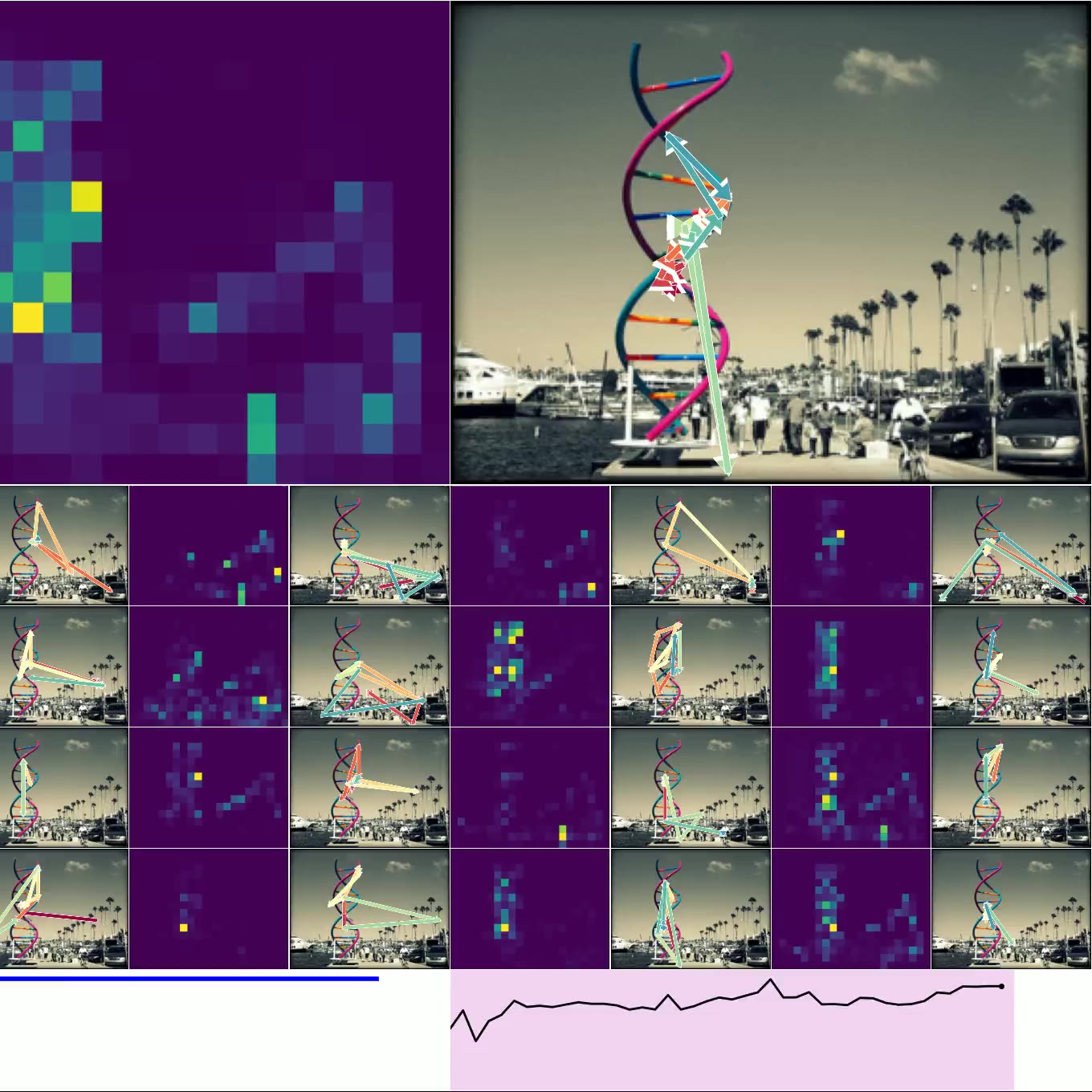
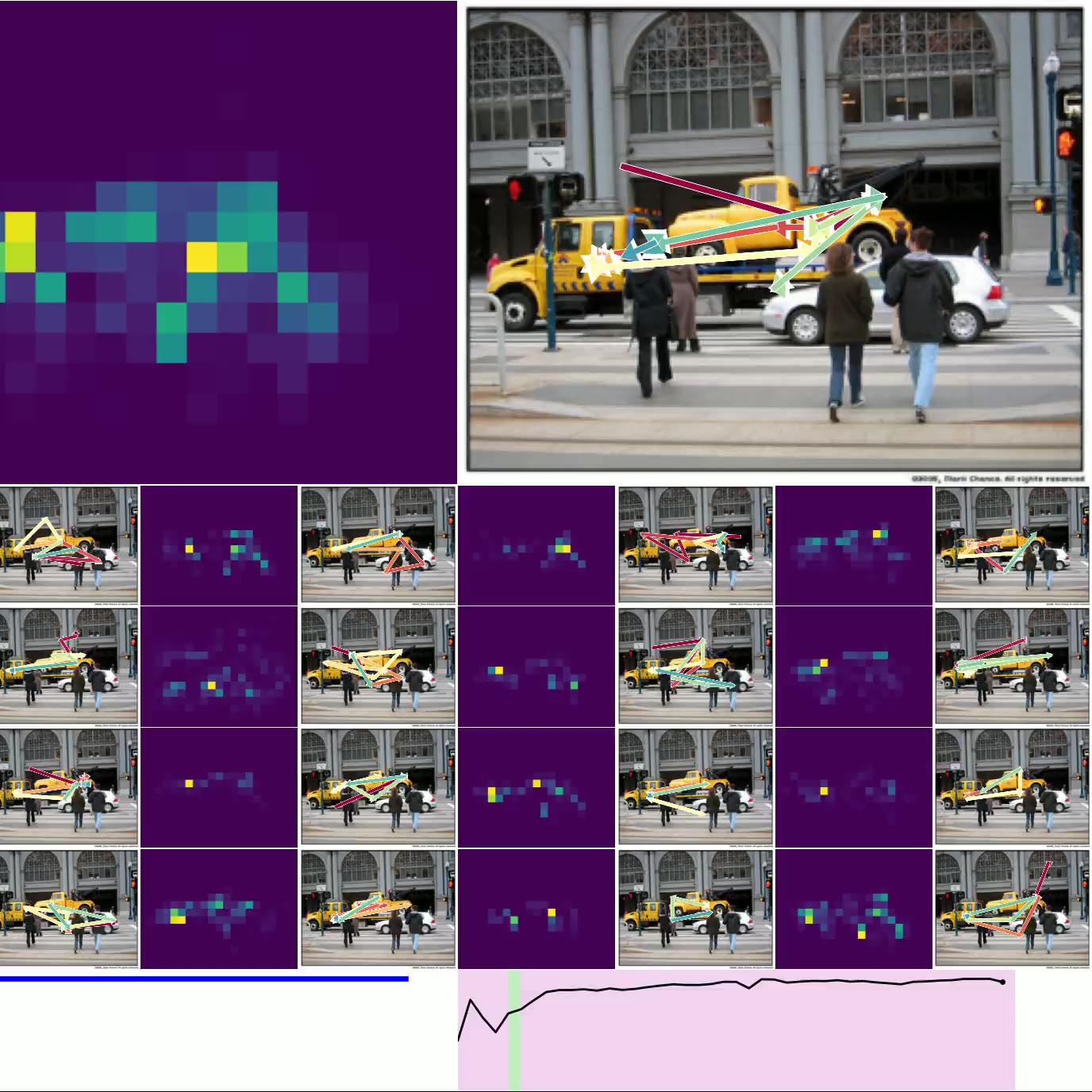
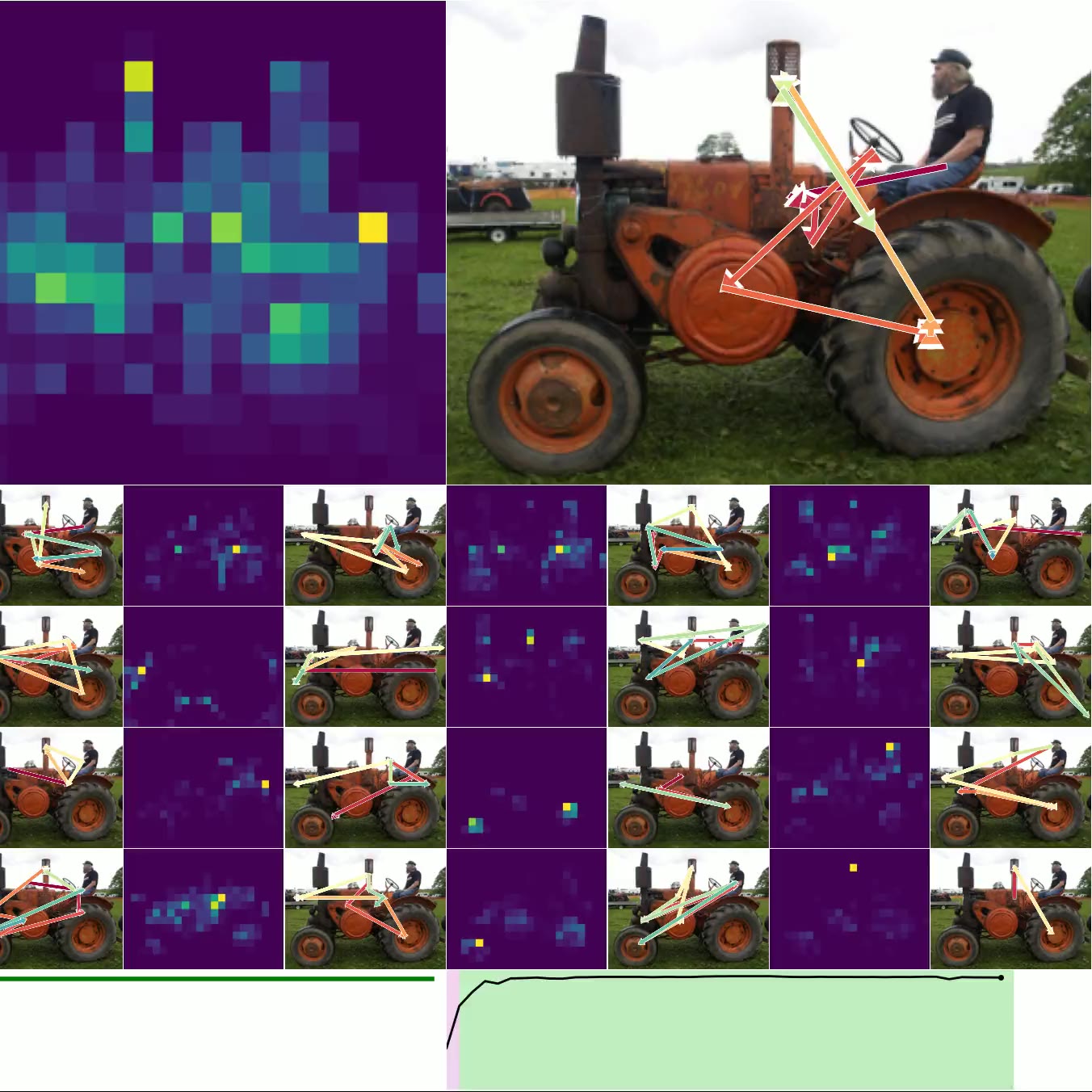
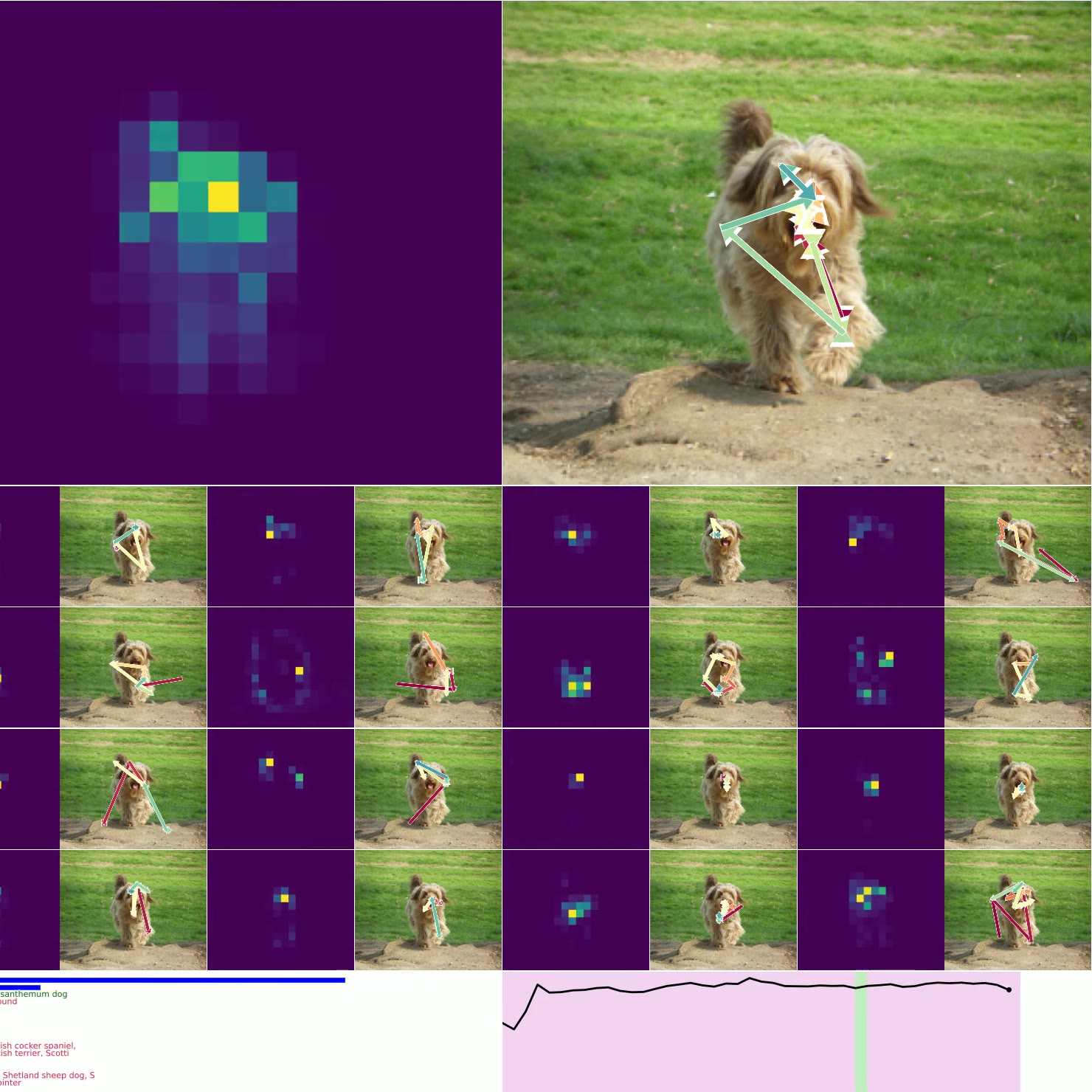图 4. 思考图像：左上方是 CTM 观察右侧图像时的平均注意力加权（显示了 16 个头）。 类预测显示在左下方，确定性显示在右下方（绿色表示正确的预测）。 底部的较小图像是用于加载其他示例的按钮，显示了各种确定性和正确性。
结果
图 5a. Top-5 准确性：使用不同的预测机制，CTM 在每个内部时钟（思考步骤）上获得不同的准确性水平。 在大约 15 个时钟时，考虑确定性是有意义的。 
图 5b. 校准：通常被认为是衡量模型与底层数据分布拟合程度的重要指标，CTM 具有非常好的校准。 
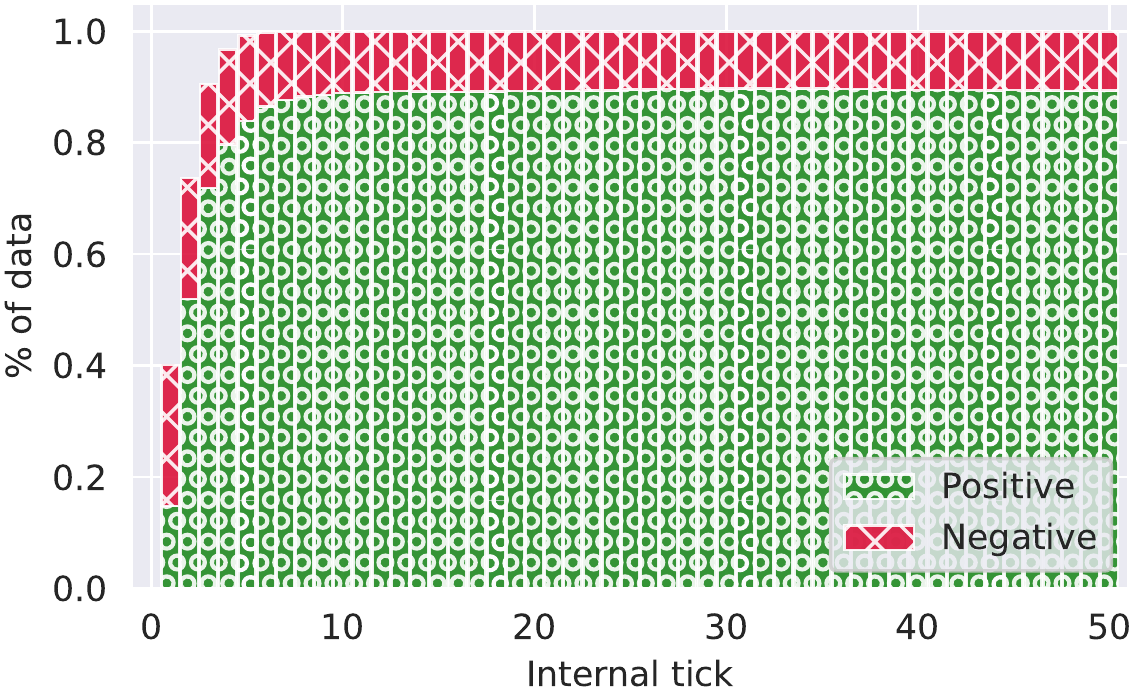图 5c. 确定性阈值=0.5：此确定性阈值下的 top-5 准确性（黑线，左侧视频的右下方）。 
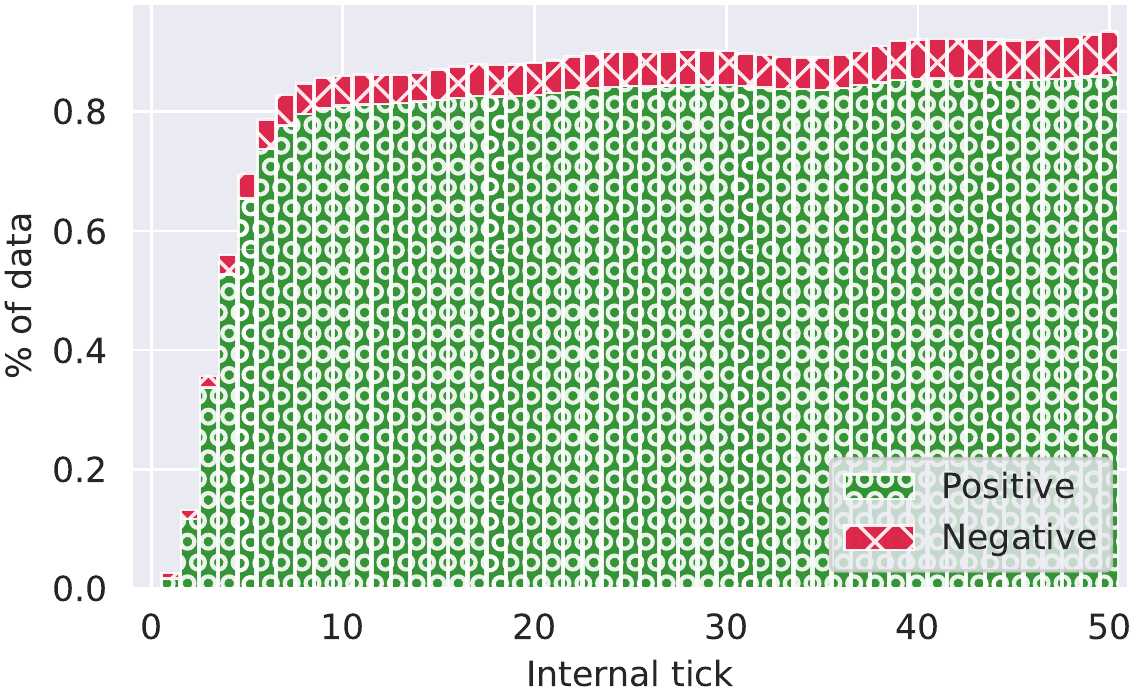图 5d. 确定性阈值=0.9：此确定性阈值下的 top-5 准确性（黑线，左侧视频的右下方）。
这是我们 ImageNet 实验的结果子集（请参阅 技术报告 以获取更多信息）。 至关重要的是，CTM 启用了 Adaptive Compute，其中内部步骤（CTM 对问题投入了多少思考）可以被缩短。 这些图显示了在缩短思考时可以预期什么样的准确性。 超过某个点只能获得边际收益，但仍然可以获得收益。
图 4. 显示了 CTM 在推理数据时所关注的位置。 我们显示了所有 16 个头的 注意力权重，并标出模型在每个头的位置（以及顶部的平均位置）。 预测显示在左下方，随时间的确定性显示在右下方。 图 6. 显示了 神经活动 的可视化，因为 CTM 思考单个图像：请注意多尺度结构以及活动似乎如何“流动”。
图 6. 神经活动：使用 UMAP 投影在 2D 中可视化。 每个神经元都显示为单个点，其大小随着绝对幅度而缩放，颜色随着值而变化（蓝色表示负值，红色表示正值）。 我们在后面的演示中显示了类似的可视化。
讨论
我们从未打算训练一个在 ImageNet 上实现一些显着的新最先进性能的模型。 经过十多年的研究，AI 研究人员已经期望 ImageNet 具有很高的性能。 相反，我们想展示 CTM 与数据的交互 是多么不同和有趣。 左侧/上方的视频演示了 CTM 执行的思考过程，这些图显示了它的好处。 让我们结合上下文来了解这里发生了什么：CTM 正在查看这些图像，同时通过直接使用 神经活动同步 作为表示来建立其预测。 我们之前展示的 神经动力学 实际上是 CTM 观察 ImageNet 的动力学示例！ 迷宫演示 中 CTM 输出的路径类似于此处进行的类预测。
缺失的成分：时间
在许多情况下，生物智能仍然优于 AI [24, 25, 5, 26]。 生物大脑解决任务的方式与传统的神经网络非常不同，这可能解释了为什么会出现这种情况。 可能是 生物智能以现代 AI 根本不使用的方式关注时间。 在这项工作中，我们的目标是开发一种模型，该模型以更符合生物大脑的方式解决问题，强调神经动力学的精确时序和相互作用的核心作用。 我们在视频演示中指出的可解释且直观的结果非常令人兴奋，因为它表明 CTM 确实正在利用时间的优势来推理数据。 有关模型超参数的详细信息，请参见 技术报告。
实验：解决 2D 迷宫 - 以困难的方式进行
原因和方式
解决迷宫对于机器来说是一项具有挑战性的任务 [27, 20, 28]，只有当前的 [最先进的模型才能在相当简单的 迷宫 上表现良好](https://pub.sakana.ai/ctm/https:/openai.com/index/thinking-with-images/)。 即使如此，现有方法要么需要仔细设计数据/目标