从零开始实现 Llama (2023): 无痛复现论文指南

Llama from scratch (2023)

Source | HN Comments

文章分享了从零开始实现 Llama 模型的经验和技巧，主要围绕以下几点展开： 1. **迭代开发：** 从小处着手，逐步构建，先实现辅助函数和简单模型，再分解论文，逐个实现并测试。 2. **验证层的功能：** 频繁使用 `.shape`、`assert` 和 `plt.imshow` 检查张量形状和计算结果，进行测试以确保每一层按预期工作。 3. **Llama 架构修改：** 逐步添加 RMSNorm、旋转嵌入和 SwiGLU 激活函数等 Llama 的关键改进，并进行测试。

Brian Kitano

首页博客

从零开始实现 Llama (或者说如何才能不崩溃地实现一篇论文)

_ 2023 年 8 月 9 日 _

从零开始实现 Llama

我想分享一些我实现论文的经验技巧。我将介绍我目前在训练用于 TinyShakespeare 的大幅缩减版 Llama 时所获得的技巧。这篇文章深受 Karpathy 的 Makemore series 的启发，我强烈推荐。

我只会大致遵循论文的布局；虽然章节的格式和顺序对于发表来说很有意义，但我们要做的是实现论文。我也会跳过一些显而易见的步骤，比如设置虚拟环境和安装依赖项。

以下是我们最终得到结果的预览：

print(generate(llama, MASTER_CONFIG, 500)[0])
ZELBETH:
Sey solmenter! 'tis tonguerered if berryishdd, and What his stabe, you, and, but all I pilJefals, mode with,
Vurint as steolated have loven OlD the queen'd refore
Are been, good plmp:
Proforne, wift'es swleen, was no bunderes'd a a quain beath!
Tybell is my gateer stalk smen'd as be matious dazest brink thou
lord
Enves were cIUll, afe and whwas seath This a is, an tale hoice his his onety Meall-tearn not murkawn, fase bettizen'd her,
To belacquesterer? baxewed wupl usweggs yet tall
An

关键要点

始终迭代工作：从小处着手，保持确定性，逐步构建。

我实现论文的方法是：

创建所有定量测试模型所需的辅助函数（数据分割、训练、绘制损失）。
在你甚至还没看论文之前，选择一个你过去做过的、小的、简单的和快速的模型。然后创建一个辅助函数来定性地评估模型。
首先分解论文的不同组成部分，然后逐个实现它们，并在进行过程中进行训练和评估。

确保你的层执行了你认为应该执行的操作。

经常使用 .shape 。assert 和 plt.imshow 也是你的好朋友。
首先不使用矩阵乘法计算出结果，然后在之后使用 torch 函数使其高效。
进行测试以确认你的层是正确的。例如，RoPE 嵌入具有你可以测试的特定属性。对于 Transformer，你可以通过查看注意力图来测试注意力是否正常工作。
在各种批量大小、序列长度和嵌入维度上测试你的层。即使它适用于一种大小，也可能不适用于其他大小，这将在推理时导致问题。

关于 Llama

Llama 是一个基于 Transformer 的语言建模模型。Meta AI 今年夏天开源了 Llama，它受到了很多关注（双关语）。在阅读介绍时，他们清楚地表明了他们的目标：使模型更便宜地运行推理，而不是优化训练成本。

现在，我们只需加载我们的库并开始。

importtorch
fromtorchimport nn
fromtorch.nnimport functional as F
importnumpyasnp
frommatplotlibimport pyplot as plt
importtime
importpandasaspd

设置我们的数据集

虽然在 Llama 中他们训练了 1.4T 个 token，但我们的数据集 TinyShakespeare，即莎士比亚所有作品的集合，大约有 1M 个字符。

lines = open('./input.txt', 'r').read()
vocab = sorted(list(set(lines)))
itos = {i:ch for i, ch in enumerate(vocab)}
stoi = {ch:i for i, ch in enumerate(vocab)}
print(lines[:30])

First Citizen:
Before we proce

他们使用 SentencePiece 字节对编码分词器，但我们将只使用一个简单的字符级分词器。

# simple tokenization by characters
defencode(s):
  return [stoi[ch] for ch in s]
defdecode(l):
  return ''.join([itos[i] for i in l])
print('vocab size:', len(vocab))
decode(encode("hello"))

vocab size: 65


'hello'

由于我们的数据集足够小，我们不需要担心如何将其存储在内存中等问题。

第一个技巧：我正在创建一个 config 对象，用于存储一些基本的模型参数。它可以使我们的代码更具可读性，并从代码中删除常量和幻数。我不会使用类型提示，因为我希望现在保持灵活性，并且能够稍后添加更多参数。

MASTER_CONFIG = {
  "vocab_size": len(vocab),
}

dataset = torch.tensor(encode(lines), dtype=torch.int8)
dataset.shape

torch.Size([1115394])

让我们创建一个方法来生成我们用于批次的训练数据和标签。我们将对验证和测试数据使用相同的方法。请注意，我喜欢在定义函数的同一代码块中测试我的函数，以确保它们在继续操作之前按预期工作。

defget_batches(data, split, batch_size, context_window, config=MASTER_CONFIG):
  train = data[:int(.8 * len(data))]
  val = data[int(.8 * len(data)): int(.9 * len(data))]
  test = data[int(.9 * len(data)):]
  
  batch_data = train
  if split == 'val':
    batch_data = val
  if split == 'test':
    batch_data = test
  
  # pick random starting points
  ix = torch.randint(0, batch_data.size(0) - context_window - 1, (batch_size,))
  x = torch.stack([batch_data[i:i+context_window] for i in ix]).long()
  y = torch.stack([batch_data[i+1:i+context_window+1] for i in ix]).long()
  return x, y
MASTER_CONFIG.update({
  'batch_size': 8,
  'context_window': 16
})
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
[(decode(xs[i].tolist()), decode(ys[i].tolist())) for i in range(len(xs))]

[(', or banishment,', ' or banishment, '),
 ('do what hands do', 'o what hands do;'),
 ("? If thou'lt see", " If thou'lt see "),
 ('and could put br', 'nd could put bre'),
 ("hath deliver'd.\n", "ath deliver'd.\nI"),
 ('ing by: whereof ', 'ng by: whereof I'),
 (' blows! Despisin', 'blows! Despising'),
 ('ng of blood, who', 'g of blood, whos')]

实现论文的有趣之处在于，模型工作有两个方面：编译（你的张量是否从一层到另一层都匹配），以及训练（损失是否降低）。弄清楚如何确保你的每个组成部分都在工作是以可预测的、以工程思维的方式开发你的模型的关键。

这就是为什么我们还要定义评估模型的方法。我们希望在甚至定义模型之前就做到这一点，因为我们希望能够使用它来评估我们正在训练的模型。

@torch.no_grad() # don't compute gradients for this function
defevaluate_loss(model, config=MASTER_CONFIG):
  out = {}
  model.eval()
  for split in ["train", "val"]:
    losses = []
    for _ in range(10):
      xb, yb = get_batches(dataset, split, config['batch_size'], config['context_window'])
      _, loss = model(xb, yb)
      losses.append(loss.item())
    out[split] = np.mean(losses)
  model.train()
  return out

设置一个可工作的基本模型

这是一个带有嵌入的基本前馈神经网络。它是我们将要从之开始的基本模型，然后逐步替换其中的部分，直到我们最终得到 Llama 中描述的模型。

classSimpleBrokenModel(nn.Module):
  def__init__(self, config=MASTER_CONFIG):
    super().__init__()
    self.config = config
    self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
    self.linear = nn.Sequential(
      nn.Linear(config['d_model'], config['d_model']),
      nn.ReLU(),
      nn.Linear(config['d_model'], config['vocab_size']),
    )
    print("model params:", sum([m.numel() for m in self.parameters()]))
  defforward(self, idx, targets=None):
    x = self.embedding(idx)
    a = self.linear(x)
    logits = F.softmax(a, dim=-1)
    if targets is not None:
      loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
      return logits, loss
    else:
      return logits
MASTER_CONFIG.update({
  'd_model': 128,
})
model = SimpleBrokenModel(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)

model params: 33217

在这一点上，我们必须开始担心张量的形状并使索引匹配。查看我们模型定义中的这一行：

loss = F.cross_entropy(logits.view(-1, config['vocab_size']), targets.view(-1))

我们必须重塑 logits 和 targets 张量，以便它们的维度在比较时匹配。我们使用 view 方法来做到这一点。-1 参数表示“从其他维度推断此维度”。因此，在这种情况下，我们说的是“重塑 logits 和 targets 以具有相同数量的行，以及使之发生所需的任意数量的列”。这是处理批量数据时的一种常见模式。

好的，让我们训练我们的 SimpleBrokenModel 以确保梯度流动。在我们确认之后，我们可以替换其中的部分以匹配 Llama，再次训练并跟踪我们的进度。正是在这个时候，我开始保存我的训练运行日志，这样我就可以轻松地返回到之前的运行，以防我搞砸了什么。

MASTER_CONFIG.update({
  'epochs': 1000,
  'log_interval': 10,
  'batch_size': 32,
})
model = SimpleBrokenModel(MASTER_CONFIG)
optimizer = torch.optim.Adam(
  model.parameters(), 
)
deftrain(model, optimizer, scheduler=None, config=MASTER_CONFIG, print_logs=False):
  losses = []
  start_time = time.time()
  for epoch in range(config['epochs']):
    optimizer.zero_grad()
    
    xs, ys = get_batches(dataset, 'train', config['batch_size'], config['context_window'])
    logits, loss = model(xs, targets=ys)
    loss.backward()
    optimizer.step()
    
    if scheduler:
      scheduler.step()
    
    if epoch % config['log_interval'] == 0:
      batch_time = time.time() - start_time
      x = evaluate_loss(model)
      losses += [x]
      if print_logs:
        print(f"Epoch {epoch} | val loss {x['val']:.3f} | Time {batch_time:.3f} | ETA in seconds {batch_time*(config['epochs']-epoch)/config['log_interval']:.3f}")
      start_time = time.time()
      if scheduler:
        print("lr: ", scheduler.get_lr())
  print("validation loss: ", losses[-1]['val'])
  return pd.DataFrame(losses).plot()
train(model, optimizer)

model params: 33217
validation loss: 3.942167806625366


<Axes: >

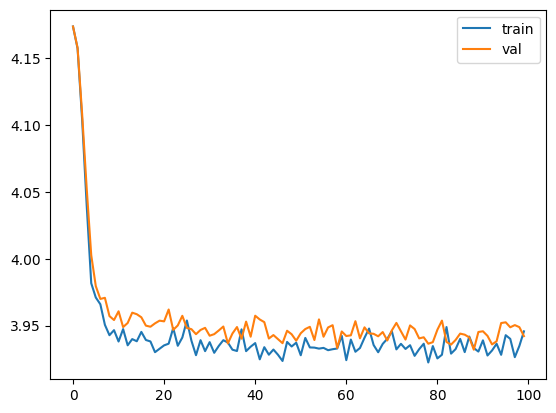png 请注意，我们获得的训练曲线会下降，但几乎没有下降。我们怎么知道它几乎没有训练？我们必须使用第一性原理。训练前的交叉熵损失为 4.17，1000 个 epoch 后为 3.93。我们如何直观地理解它？

在这种情况下，交叉熵指的是我们有多大可能选错单词。因此， H(T,q)=−∑i=1N1Nlogq(xi) 其中 q(xi) 是模型估计的挑选正确单词的概率。如果 q(xi) 接近 1，则 logq 接近 0；类似地，如果 q 很小，则 logq 是一个很大的负数，因此 −logq 将是一个很大的正数。现在建立直觉：首先，−logq=4.17，因此 q=0.015，或约为 164.715。回想一下，词汇量的大小 |V|=65，所以我们基本上在这里说的是，该模型在选择下一个字母方面与从我们的词汇表中随机挑选一样好。训练后，−logq=3.93，因此我们现在基本上是在 50 个字母之间进行选择。这是一个非常小的改进，所以可能出了问题。

要了解损失与模型性能之间的关系，请考虑模型在 V~ 个 token 之间进行选择；当 V~ 很小时，模型更有可能猜对。此外，我们知道 maxV~=V，这可以帮助我们了解我们的模型是否在学习。 V~=exp(L) 让我们尝试调试发生了什么。请注意，在我们的模型中，我们正在 logits 上使用 softmax 层，该函数接受一个数字向量并将它们压缩为概率分布。但是对于使用内置的 F.cross_entropy 函数，我们需要直接传入未归一化的 logits。因此，让我们从我们的模型中删除它并重试。

classSimpleModel(nn.Module):
  def__init__(self, config):
    super().__init__()
    self.config = config
    self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
    self.linear = nn.Sequential(
      nn.Linear(config['d_model'], config['d_model']),
      nn.ReLU(),
      nn.Linear(config['d_model'], config['vocab_size']),
    )
    print("model params:", sum([m.numel() for m in self.parameters()]))
  defforward(self, idx, targets=None):
    x = self.embedding(idx)
    logits = self.linear(x)
    if targets is not None:
      loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
      return logits, loss
    else:
      return logits
model = SimpleModel(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer)

model params: 33217
validation loss: 2.5058052778244018


<Axes: >

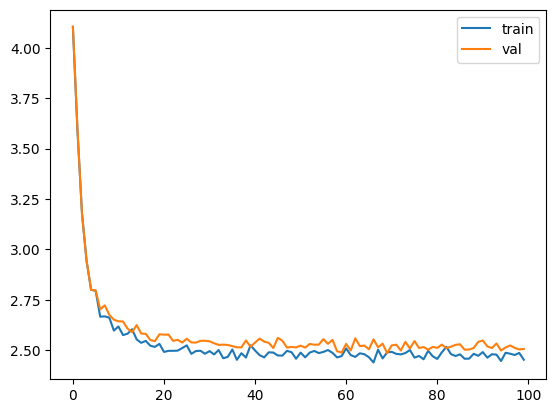png 太好了，现在我们的损失为 2.54，因此我们从 12.67 个字符中进行选择。这比我们开始时的 65 个好多了。让我们向我们的模型添加一个生成方法，以便我们直观地看到我们模型的结果。

defgenerate(model, config=MASTER_CONFIG, max_new_tokens=30):
  idx = torch.zeros(5, 1).long()
  for _ in range(max_new_tokens):
    # call the model
    logits = model(idx[:, -config['context_window']:])
    last_time_step_logits = logits[
      :, -1, :
    ] # all the batches (1), last time step, all the logits
    p = F.softmax(last_time_step_logits, dim=-1) # softmax to get probabilities
    idx_next = torch.multinomial(
      p, num_samples=1
    ) # sample from the distribution to get the next token
    idx = torch.cat([idx, idx_next], dim=-1) # append to the sequence
  return [decode(x) for x in idx.tolist()]
generate(model)

['\nFind!\nD:\nAr t,\nLis sthte o t l',
 '\nAnd ronnot ar\nBE:\nKINRDYOrspr;',
 '\nI t athe momyengthend thanswal',
 '\nFis t bp he\nLacarn.\nA:\nYOMI wi',
 '\nWh ly sck\nB-de pll t\nHERIns ou']

它不算太坏，但也不算太好。但是现在我们有一个可以训练到验证损失的工作模型。因此，在这里我们将迭代我们的模型，使其更接近 Llama。

Llama 细节

Llama 描述了对原始 Transformer 的三个架构修改：

用于预归一化的 RMSNorm
旋转嵌入
SwiGLU 激活函数

我们将一次向我们的基本模型添加一个，并进行迭代。

RMSNorm

在 Vaswani 2017 中，原始 transformer 使用 BatchNormalization。在 Llama 中，作者使用 RMSNorm，在这种情况下，你可以通过方差缩放 bector 而无需将其居中。此外，虽然 Vaswani 将归一化应用于注意力层的输出（后归一化），但 Llama 将其应用于之前的输入（预归一化）。

classRMSNorm(nn.Module):
  def__init__(self, layer_shape, eps=1e-8, bias=False):
    super(RMSNorm, self).__init__()
    self.register_parameter("scale", nn.Parameter(torch.ones(layer_shape)))
  defforward(self, x):
"""
    assumes shape is (batch, seq_len, d_model)
    """
    # frob norm is not the same as RMS. RMS = 1/sqrt(N) * frob norm
    ff_rms = torch.linalg.norm(x, dim=(1,2)) * x[0].numel() ** -.5
    raw = x / ff_rms.unsqueeze(-1).unsqueeze(-1)
    return self.scale[:x.shape[1], :].unsqueeze(0) * raw
config = {
  'batch_size': 5,
  'context_window': 11,
  'd_model': 13,
}
batch = torch.randn((config['batch_size'], config['context_window'], config['d_model']))
m = RMSNorm((config['context_window'], config['d_model']))
g = m(batch)
print(g.shape)

torch.Size([5, 11, 13])

我们想要进行测试以确保 RMSNorm 正在执行我们认为应该执行的操作。我们可以通过传统方式：逐行比较来做到这一点。RMSNorm 具有一个属性，即层的范数将是层中元素数量的平方根，因此我们可以检查每个层。

rms = torch.linalg.norm(batch, dim=(1,2)) * (batch[0].numel() ** -.5)
# scaled_batch.var(dim=(1,2))
assert torch.linalg.norm( torch.arange(5).float() ) == (torch.arange(5).float() ** 2 ).sum() ** .5
rms = torch.linalg.norm( torch.arange(5).float() ) * (torch.arange(5).numel() ** -.5)
assert torch.allclose(torch.linalg.norm(torch.arange(5).float() / rms), torch.tensor(5 ** .5))
ff_rms = torch.linalg.norm(batch, dim=(1,2)) * batch.shape[1:].numel() ** -.5
# RMS for sure
ffx = torch.zeros_like(batch)
for i in range(batch.shape[0]):
  ffx[i] = batch[i] / ff_rms[i]
assert torch.allclose(torch.linalg.norm(ffx, dim=(1,2)) ** 2, torch.tensor(143).float())
assert torch.allclose(ffx, g)

好的，这就是 RMSNorm，看起来它正在工作。再次，让我们测试一下。

classSimpleModel_RMS(nn.Module):
  def__init__(self, config):
    super().__init__()
    self.config = config
    self.embedding = nn.Embedding(config['vocab_size'], config['d_model'])
    self.rms = RMSNorm((config['context_window'], config['d_model']))
    self.linear = nn.Sequential(
      nn.Linear(config['d_model'], config['d_model']),
      nn.ReLU(),
      nn.Linear(config['d_model'], config['vocab_size']),
    )
    print("model params:", sum([m.numel() for m in self.parameters()]))
  defforward(self, idx, targets=None):
    x = self.embedding(idx)
    x = self.rms(x) # rms pre-normalization
    logits = self.linear(x)
    if targets is not None:
      loss = F.cross_entropy(logits.view(-1, self.config['vocab_size']), targets.view(-1))
      return logits, loss
    else:
      return logits
model = SimpleModel_RMS(MASTER_CONFIG)
xs, ys = get_batches(dataset, 'train', MASTER_CONFIG['batch_size'], MASTER_CONFIG['context_window'])
logits, loss = model(xs, ys)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer)

model params: 35265
validation loss: 2.5015316724777223


<Axes: >

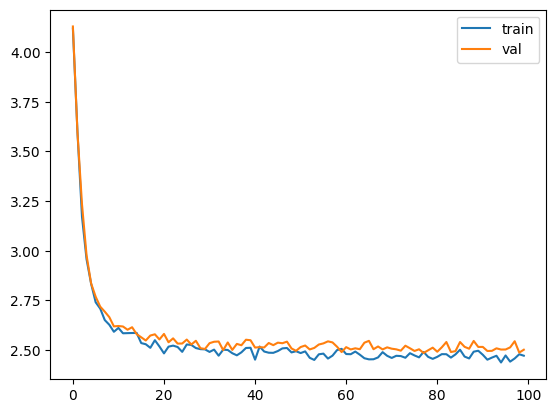png 因此 RMSNorm 有效，并且使我们的损失降低了一小部分。

旋转嵌入

RoPE 是 transformer 的一种位置编码。在 Attention is All You Need 中，作者提出了两种位置编码，学习的和固定的。在 RoPE 中，作者建议通过旋转嵌入来嵌入 token 在序列中的位置，每个位置都有不同的旋转。

defget_rotary_matrix(context_window, embedding_dim):
  R = torch.zeros((context_window, embedding_dim, embedding_dim), requires_grad=False)
  for position in range(context_window):
    for i in range(embedding_dim//2):
      theta = 10000. ** (-2.*(i - 1) / embedding_dim)
      m_theta = position * theta
      R[position, 2*i,2*i] = np.cos(m_theta)
      R[position, 2*i,2*i+1] = - np.sin(m_theta)
      R[position, 2*i+1,2*i] = np.sin(m_theta)
      R[position, 2*i+1,2*i+1] = np.cos(m_theta)
  return R

K = 3
config = {
  'batch_size': 10,
  'd_model': 32,
  'n_heads': 8,
  'context_window': K**2,
}
batch = torch.randn(1, config['context_window'], config['d_model'])
R = get_rotary_matrix(config['context_window'], config['d_model'])
fig, ax = plt.subplots(K, K, figsize=(K * 3, K * 4))
for i in range(K):
  for j in range(K):
    ax[i, j].imshow(R[i * K + j, :, :].detach().numpy())
    ax[i, j].set_title(f'rotation at {i*K+j}')

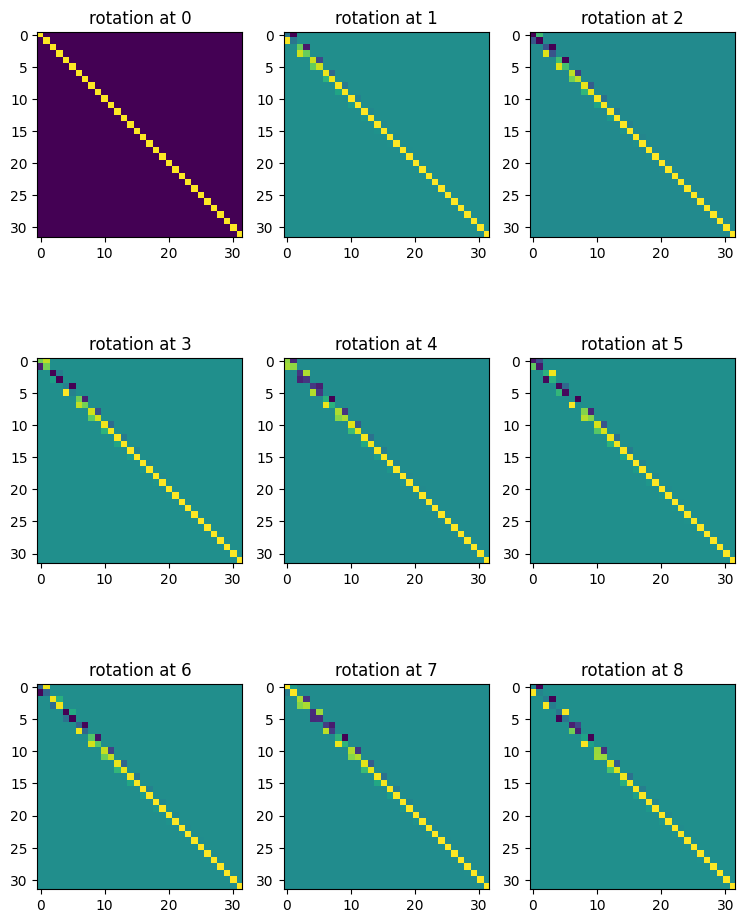png 让我们确保这些有效。它们应该表现出以下质量： qmTkn=(RΘ,mdWqxm)T(RΘ,ndWkxn)=xTWqRΘ,n−mdWkxn.

config = {
  'd_model': 128,
  'context_window': 16,
}
R = get_rotary_matrix(config['context_window'], config['d_model'])
x = torch.randn(config['d_model'])
y = torch.randn(config['d_model'])
m = 3
n = 13
x_m = R[m,:,:] @ x
x_n = R[n,:,:] @ y
assert torch.isclose(x_m @ x_n, x @ R[n-m,:,:] @ y)

因此 RoPE 旋转按预期工作。

config = {
  'batch_size': 10,
  'd_model': 512,
  'n_heads': 8,
  'context_window': 16,
}
classRoPEAttentionHead(nn.Module):
  def__init__(self, config):
    super().__init__()
    self.config = config
    self.w_q = nn.Linear(config['d_model'], config['d_model'], bias=False)
    self.w_k = nn.Linear(config['d_model'], config['d_model'], bias=False)
    self.w_v = nn.Linear(config['d_model'], config['d_model'], bias=False)
    self.R = get_rotary_matrix(config['context_window'], config['d_model'])
  defget_rotary_matrix(context_window, embedding_dim):
    R = torch.zeros((context_window, embedding_dim, embedding_dim), requires_grad=False)
    for position in range(context_window):
      for i in range(embedding_dim//2):
        theta = 10000. ** (-2.*(i - 1) / embedding_dim)
        m_theta = position * theta
        R[position, 2*i,2*i] = np.cos(m_theta)
        R[position, 2*i,2*i+1] = - np.sin(m_theta)
        R[position, 2*i+1,2*i] = np.sin(m_theta)
        R[position, 2*i+1,2*i+1] = np.cos(m_theta)
    return R
  
  defforward(self, x, return_attn_weights=False):
    b,m,d = x.shape
    
    q = self.w_q(x)
    k = self.w_k(x)
    v = self.w_v(x)
    q_rotated = (torch.bmm(q.transpose(0,1), self.R[:m])).transpose(0,1)
    k_rotated = (torch.bmm(k.transpose(0,1), self.R[:m])).transpose(0,1)
    activations = F.scaled_dot_product_attention(
      q_rotated,k_rotated,v,dropout_p =.1
    )
    if return_attn_weights:
      attn_weights = torch.bmm(q_rotated, k_rotated.transpose(1,2)) / np.sqrt(d)
      attn_weights = F.softmax(attn_weights, dim=-1)
      return activations, attn_weights
    return activations
layer = RoPEAttentionHead(config)
batch = torch.randn((config['batch_size'], config['context_window'], config['d_model']))
output, attn_weights = layer(batch, return_attn_weights=True)

提示：了解训练时张量维度与推理时张量维度之间的差异。虽然在训练时，你可以期望你的张量维度与你的模型参数紧密匹配，例如 batch.shape = (config['batch_size'], config['context_window'], config['d_model'])，但在推理时，你可能必须处理单个示例，例如 batch.shape = (1, 1, config['d_model'])。因此，你需要确保在 forward 传递中进行索引时，你是使用从输入派生的形状进行索引，而不一定是模型参数。

让我们确保它执行了我们认为它执行的操作。对于这一层，我们将要测试三件事：

它以我们认为的方式旋转嵌入
用于因果注意力的注意力掩码正常工作。

x = torch.randn((config['batch_size'], config['context_window'], config['d_model']))
q = layer.w_q(x)
k = layer.w_k(x)
v = layer.w_v(x)
q_rotated = torch.zeros_like(x)
k_rotated = torch.zeros_like(x)
v_rotated = torch.zeros_like(x)
for position in range(config['context_window']):
  q_rotated[:,position,:] = torch.matmul(q[:,position,:], layer.R[position,:,:])
  k_rotated[:,position,:] = torch.matmul(k[:,position,:], layer.R[position,:,:])
  v_rotated[:,position,:] = torch.matmul(v[:,position,:], layer.R[position,:,:])
q_rotated = (torch.bmm(q.transpose(0,1), layer.R)).transpose(0,1)
k_rotated = (torch.bmm(k.transpose(0,1), layer.R)).transpose(0,1)
v_out = (torch.bmm(v.transpose(0,1), layer.R)).transpose(0,1)
assert torch.allclose(q.transpose(0,1)[0], q[:,0,:])
assert torch.allclose(q.transpose(0,1)[0] @ layer.R[0], q[:,0,:] @ layer.R[0])
assert torch.allclose(q_rotated, q_rotated)

config = {
  'batch_size': 1,
  'd_model': 2,
  'n_heads': 2,
  'context_window': 3,
}
layer = RoPEAttentionHead(config)
batch = torch.ones((config['batch_size'], config['context_window'], config['d_model']))
output, attn_weights = layer(batch, return_attn_weights=True)
m = 0
x_q = batch[0, m]
q = layer.R[m,:,:] @ layer.w_q(x_q)
assert torch.allclose(layer.w_q(x_q), layer.w_q.weight @ x_q)
assert torch.allclose(q, layer.R[m, :, :] @ layer.w_q.weight @ x_q)
n = 2
x_k = batch[0, n]
k = layer.R[n,:,:] @ layer.w_k(x_k)
assert torch.allclose(layer.w_k(x_k), layer.w_k.weight @ x_k)
assert torch.allclose(k, layer.R[n, :, :] @ layer.w_k.weight @ x_k)
assert q.T @ k == q @ k # transpose is redundant
assert torch.allclose(q @ k, x_k.T @ layer.w_k.weight.T @ layer.R[n, :, :].T @ layer.R[m, :, :] @ layer.w_q.weight @ x_q)
assert torch.allclose(q @ k, x_k.T @ layer.w_k.weight.T @ layer.R[n-m, :, :].T @ layer.w_q.weight @ x_q)

/var/folders/w4/2j887mvs097bkhhjpgfzjlyr0000gn/T/ipykernel_52564/2062321511.py:26: UserWarning: The use of `x.T` on tensors of dimension other than 2 to reverse their shape is deprecated and it will th