墙上挂了 12 年的分形:一个 Linear Algebra 的视角
Chris K. W.
计算机相关的东西
Home Doodles Stuff About

墙上挂了 12 年的分形:一个 Linear Algebra 的视角
May 21, 2025 内容警告: 数学,胡说八道
中学时,我花了很多时间涂鸦,而不是做其他中学生应该做的事情。在画“Cool S”和 Penrose 三角形之间,我偶然发现了一种通过重复组合和复制正方形来填充方格纸的巧妙方法。我怀疑涂鸦还有更多的东西,但不太确定如何分析它。我决定委托给一个懂得更多数学的未来版本的我,于是我把它贴在书桌后面的墙上,它从高中到大学再到今天一直跟着我。
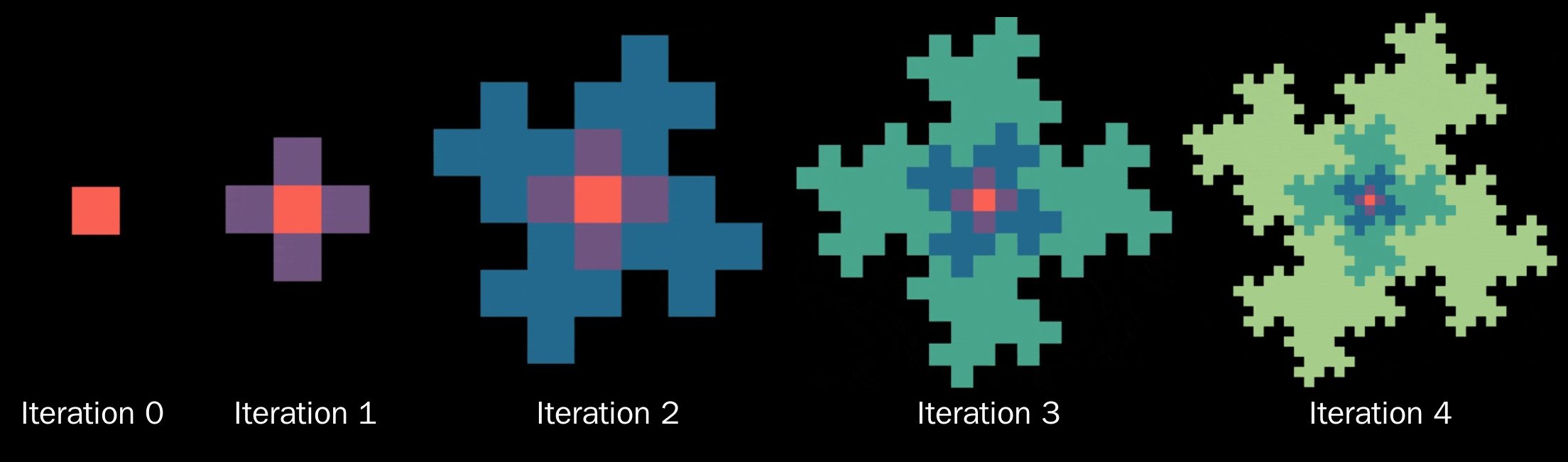
总之,经过一系列偶然事件,我现在是那个被预言的、懂得更多数学的未来版本的我。由于其花瓣状的绽放结构,以及用透明胶带贴在我墙上的悠久历史,我将亲切地称这个分形为“wallflower(墙花)”,尽管在下文中我们会看到它与一些著名的分形密切相关。为了开始研究它,回顾一下中学时的我最初是如何绘制它的可能会有所帮助:
- 从一个正方形开始。
- 将当前状态的四个副本平铺到当前状态的左侧、右侧、顶部和底部。
- 将当前状态的四个副本以略微倾斜(顺时针方向约 27 度)的角度平铺到当前状态的左侧、右侧、顶部和底部。
- 在步骤 2 和步骤 3 之间交替,直到用完方格纸。
动画形式:
 感谢 manim 和 3Blue1Brown 使这个和许多其他可视化成为可能!
感谢 manim 和 3Blue1Brown 使这个和许多其他可视化成为可能!
与 Gosper Curve 类似,可以重复运行这些步骤以最终覆盖平面的任何部分,并且每个中间状态都可以平铺平面。如果您有方格纸和空闲时间,您可以自己尝试这些步骤——翻译和跟踪先前状态的轮廓,并看着事物像拼图一样锁定到位,这很有趣。或者,一年多前我意识到可以使用 L-System 生成轮廓。规则很简单,仅包含 90 度右转 (\(R\)) 和左转 (\(L\)):
- 从 4 个右转开始:\(RRRR\)
- 每次迭代运行以下替换:\(R \rightarrow RLR, L \rightarrow RLL\)
例如,在应用第一次迭代的替换后,您应该得到 \(RLRRLRRLRLR\)。以下图像演示了该规则的前几次应用:
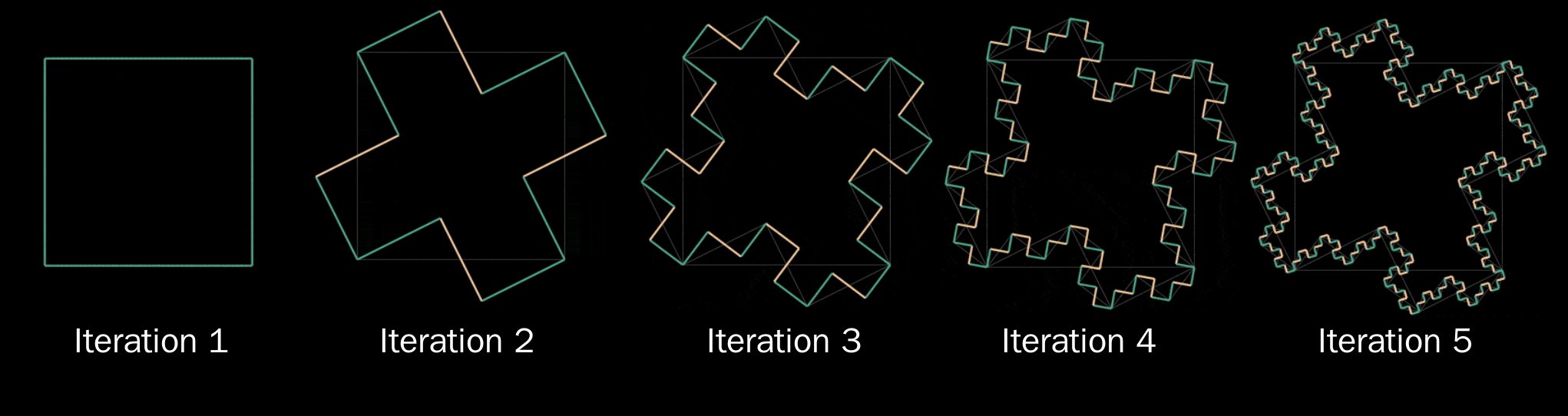 黄色=下一次转弯(顺时针方向)将向左,蓝色=向右
动画形式:
黄色=下一次转弯(顺时针方向)将向左,蓝色=向右
动画形式:
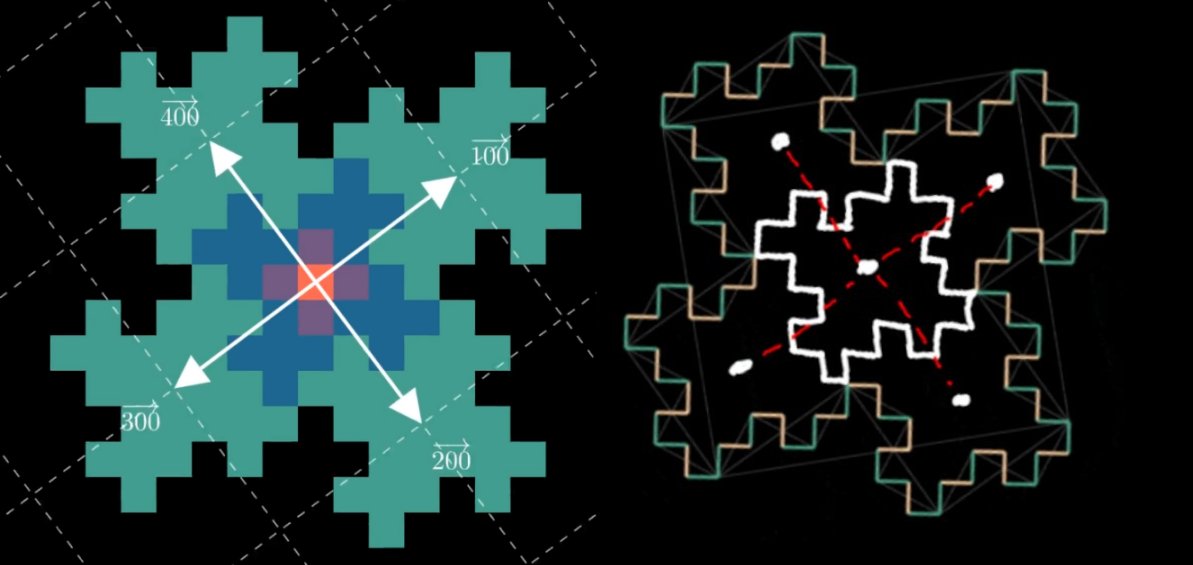
 两种方法最终都会生成等效的…等等!一年前我第一次尝试 L-System 方法时,我 以为 它生成的轮廓与 wallflower 相同。换句话说,我试图徒手绘制第四次迭代及其许多直角,然后半途而废,心想“好吧,它在前 3 次迭代中有效,因此它通常有效 \(\text{Q.E.D.}\)” 直到我开始为这篇文章制作动画时,我才意识到两者并不完全匹配。比较每种方法的第 4 次迭代:
两种方法最终都会生成等效的…等等!一年前我第一次尝试 L-System 方法时,我 以为 它生成的轮廓与 wallflower 相同。换句话说,我试图徒手绘制第四次迭代及其许多直角,然后半途而废,心想“好吧,它在前 3 次迭代中有效,因此它通常有效 \(\text{Q.E.D.}\)” 直到我开始为这篇文章制作动画时,我才意识到两者并不完全匹配。比较每种方法的第 4 次迭代:
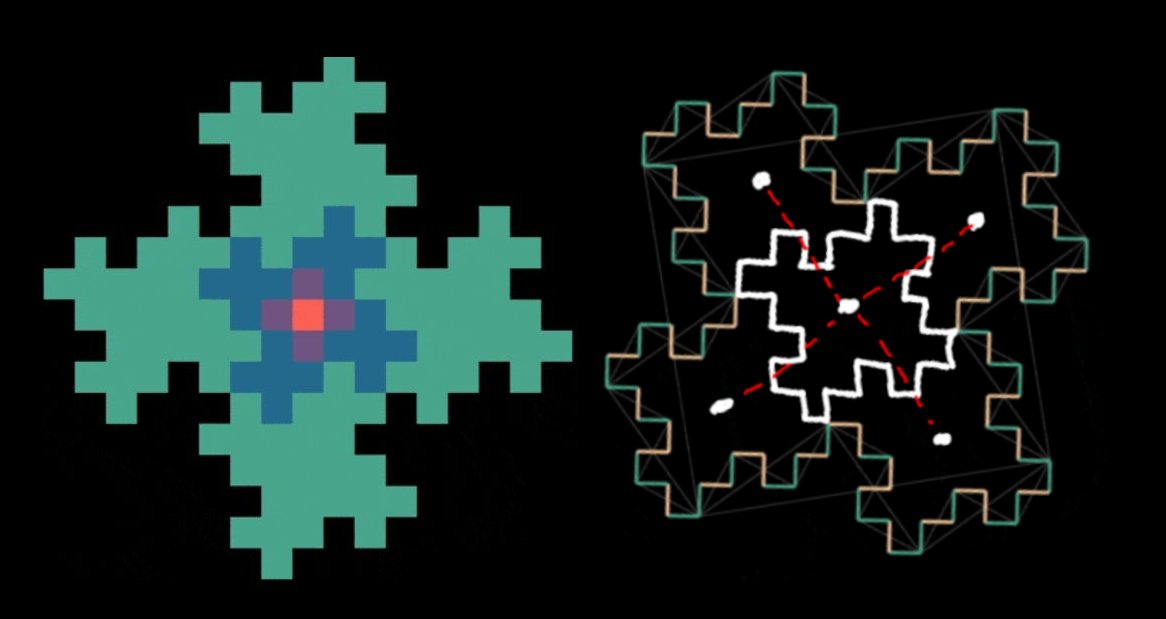 并排比较,两者之间的主要区别在于第三次迭代的“副本”围绕中心原始迭代的放置方式。“拖放”的第一种方法将副本直接放置在中心的上方、下方等,而 L-System 方法将它们对角放置。L-System 方法产生的轮廓已经记录在几个地方:
并排比较,两者之间的主要区别在于第三次迭代的“副本”围绕中心原始迭代的放置方式。“拖放”的第一种方法将副本直接放置在中心的上方、下方等,而 L-System 方法将它们对角放置。L-System 方法产生的轮廓已经记录在几个地方:
- List of fractals 的 Wikipedia 文章(列为“Quadratic von Koch island”)
- Koch snowflake 的 Wikipedia 文章(列为“Quadratic Flake”,文件名为“Karperien Flake”)
- Minkowski Sausage 的 Wikipedia 文章
- Jeffrey Ventrella 的 Mandelbrot’s Quartet 生成器
同时,通过 Google 图片搜索和 Wikipedia 冲浪,我找不到任何地方出现通过拖放方法制作的变体。为什么一种方法比另一种方法更常见?经过一番摸索,我找到了生成墙上分形版本的规则 (\(L \rightarrow RLR, R \rightarrow LLR\)),但是它们有一个奇怪的效果,似乎在每个步骤都“翻转”了您绘制轮廓的方向,例如,第一步从 \(RRRR\)(大多数是右转)变为 \(LLRLLRLLRLLR\)(大多数是左转)。另一个自然的问题是,如果原始 L-System 没有将副本与轴对齐,那么它将它们放置在什么角度?事实证明,“翻转”行为、L-System 的角度以及一开始看似任意的“大约 27 度”以一种令人惊讶的方式联系在一起。但在我们开始讨论这个问题之前,让我们先回顾一个重要的主题:
如何计数
拖延了十多年,让我有很多机会以新的视角看待分形,因为我接触了新的数学分支。大学一年级时,我学会了如何使用 Cantor pairing function,通过在笛卡尔平面上“燕尾式”移动来证明自然数 \(\mathbb{N}\) 的基数等于自然数对 \(\mathbb{N}^2\) 的基数。同样,我了解到您可以将自然数映射到螺旋线上以表明 \(\mathbb{N}\) 具有与整数对 \(\mathbb{Z}^2\) 相同的基数。
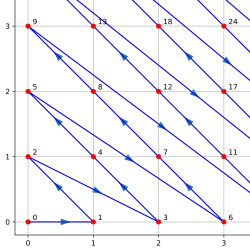
 Cantor pairing function 图像感谢 Wikipedia,螺旋线感谢 UCB CS70
Cantor pairing function 图像感谢 Wikipedia,螺旋线感谢 UCB CS70
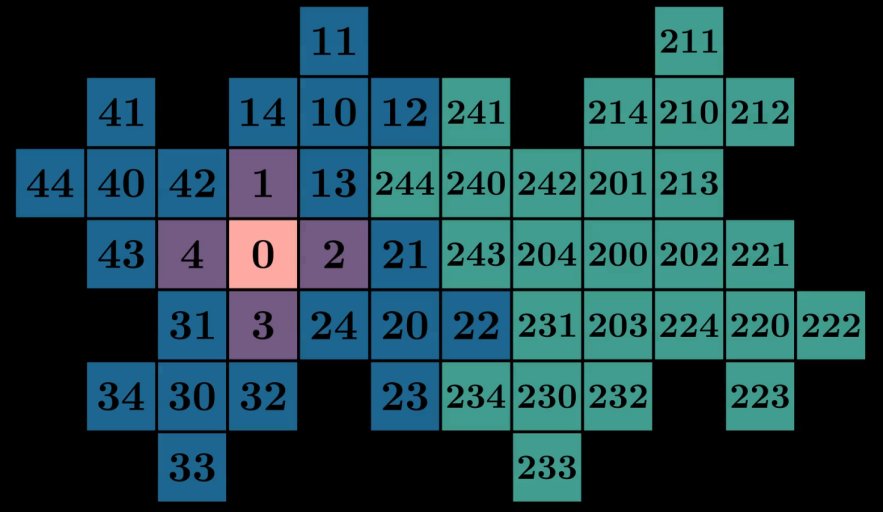
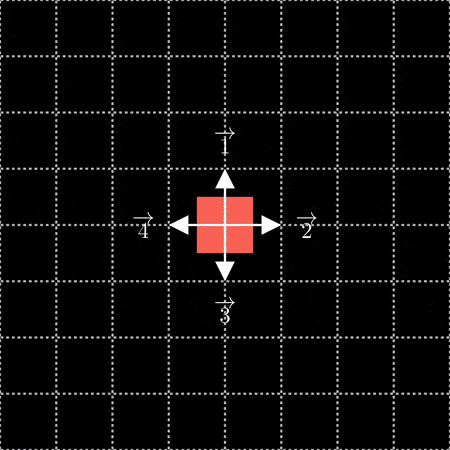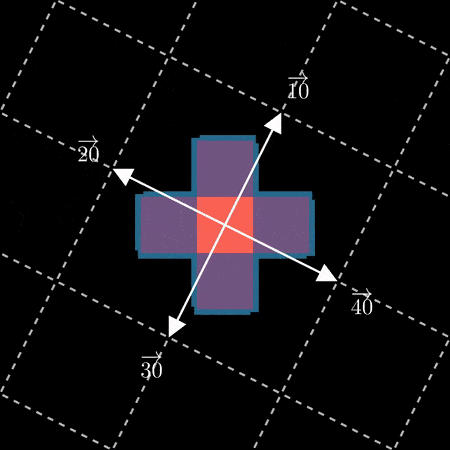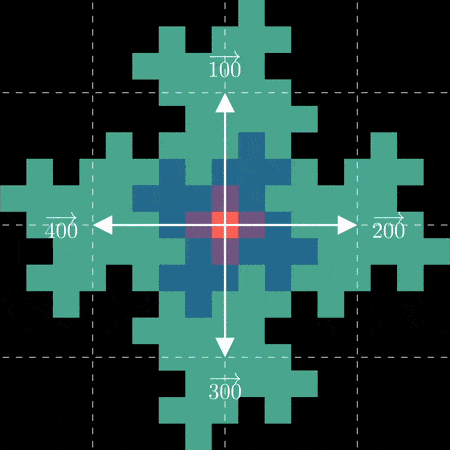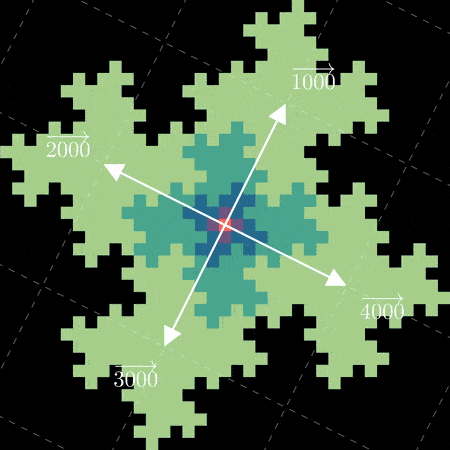
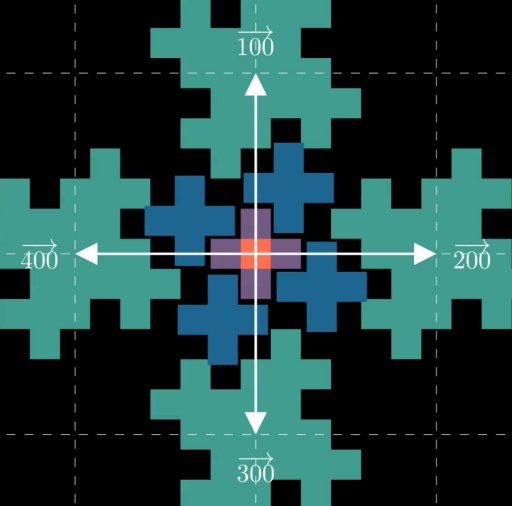
这两个都让我想起了 wallflower 如何通过从原点向外构建来填充笛卡尔平面上的空间。为了使用 wallflower 的结构作为配对函数,我们需要找到一种在放置每个正方形时分配“顺序”的方法,最好是以一种补充其递归构造性质的方式。一个自然的起点是将分形的中心用作 0。从那里,我们可以按顺时针顺序将第一次迭代中添加的周围四个正方形编号为 1、2、3 和 4:
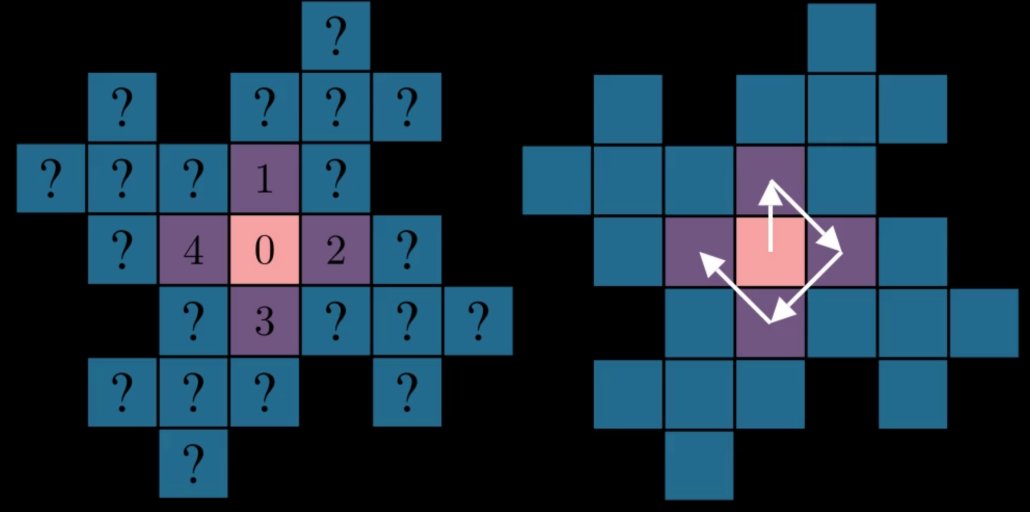
现在我们面临的问题是如何标记下一次迭代的正方形。一种方法是按照它们从上到下、从左到右出现的顺序对它们进行编号:
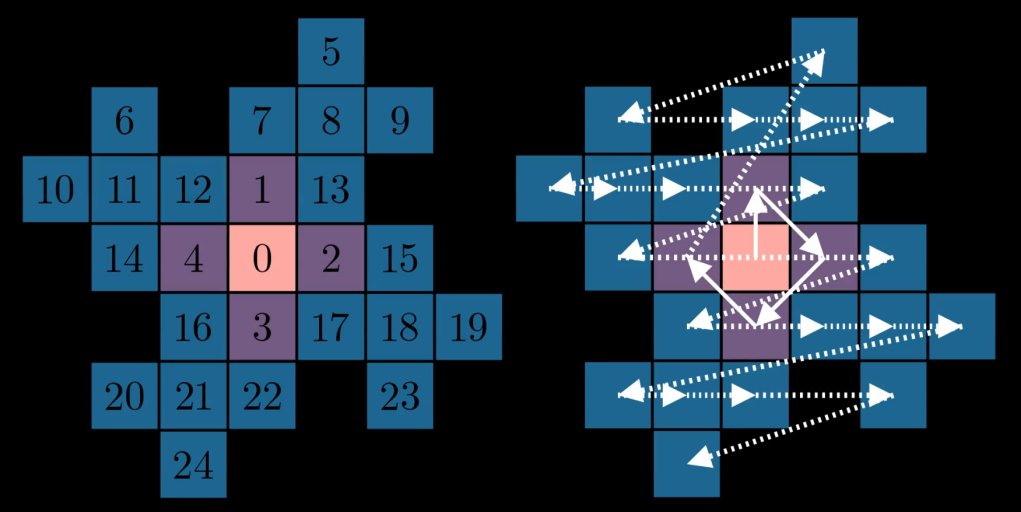 因为缺乏更好的词,所以这感觉不是很分形——这里的顺序似乎与分形的递归结构无关。如果我们尝试重用用于 0 到 4 的“从中间向外”的方法怎么办?毕竟,每个“花瓣”是我们已经给出顺序的第一次迭代的副本。在每个蓝色花瓣中以及 跨 每个蓝色花瓣(虚线)重用从 0 到 4 的顺时针方案:
因为缺乏更好的词,所以这感觉不是很分形——这里的顺序似乎与分形的递归结构无关。如果我们尝试重用用于 0 到 4 的“从中间向外”的方法怎么办?毕竟,每个“花瓣”是我们已经给出顺序的第一次迭代的副本。在每个蓝色花瓣中以及 跨 每个蓝色花瓣(虚线)重用从 0 到 4 的顺时针方案:
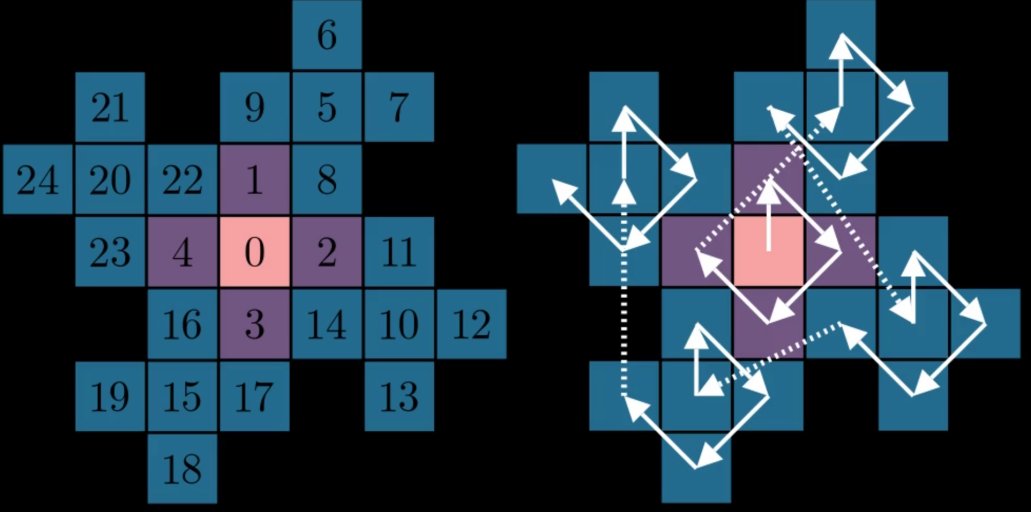 并扩展到下一组花瓣:
并扩展到下一组花瓣:
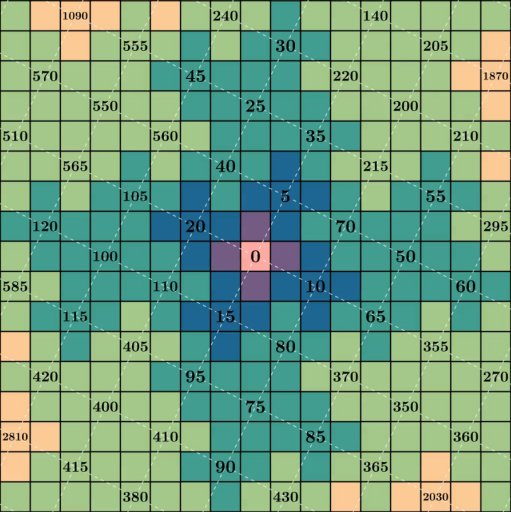
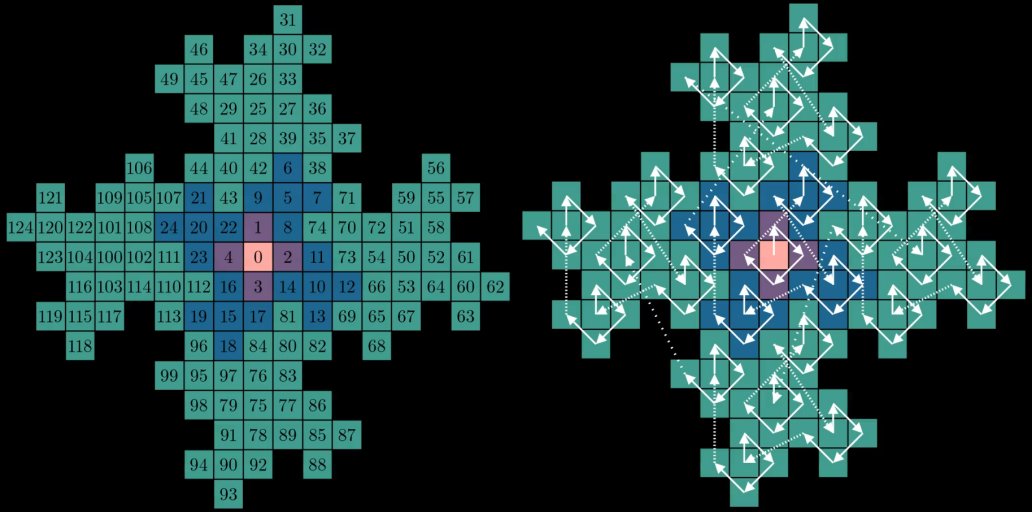 乍一看可能看起来很混乱,但如果我们查看某些数字的位置,就会出现一些有趣的属性。如果我们只将视图隔离到 5 的倍数,则会形成一个按比例放大的网格,顺时针倾斜约 27 度:
乍一看可能看起来很混乱,但如果我们查看某些数字的位置,就会出现一些有趣的属性。如果我们只将视图隔离到 5 的倍数,则会形成一个按比例放大的网格,顺时针倾斜约 27 度:
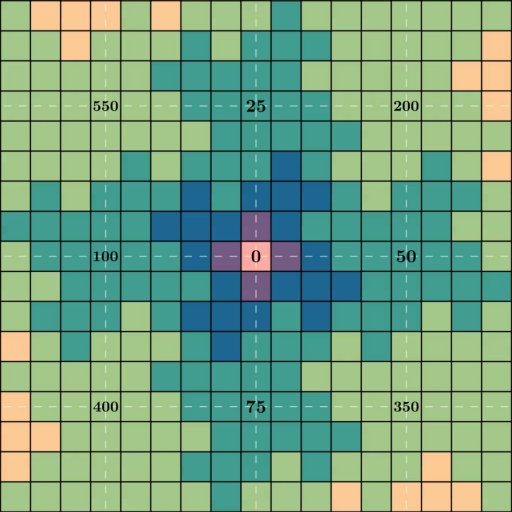
如果我们只看 \(5n + 1\) 形式的数字,我们会得到先前的网格,但向上移动了 1 个正方形:

如果我们只看 25 的倍数,我们会得到另一个网格,进一步放大:
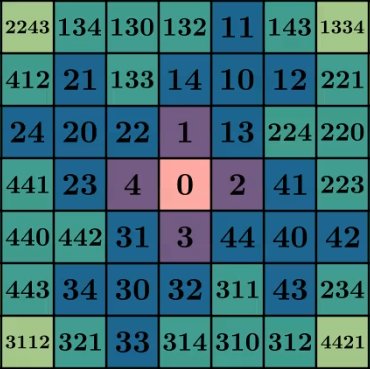
数字 5 似乎与分形有特殊的关系。如果您查看每次迭代中正方形的数量,原因就会显而易见。第 0 次迭代是单个正方形,第一次迭代有 5 个,第二次迭代有 25 个,第三次迭代有 125 个,依此类推……由于每次迭代都是通过获取先前的状态并添加 4 个附加副本来构造的,因此每一步都按 5 的因子放大。鉴于与 5 的倍数和 5 的幂的特殊关系,很容易重做标签,同时以 5 为基数而不是以 10 为基数进行计数。这样做,我们得到这个:
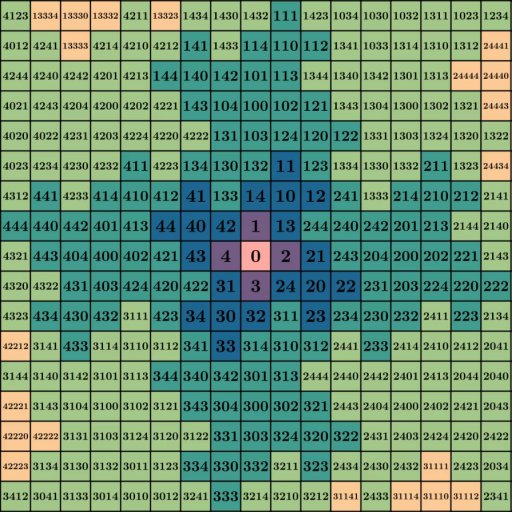
这里有很多信息,但如果我们专注于迭代 3 模式及其右侧的副本,您可能会注意到一些有趣的事情:
如何相加
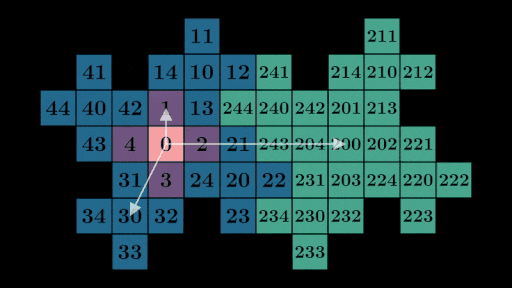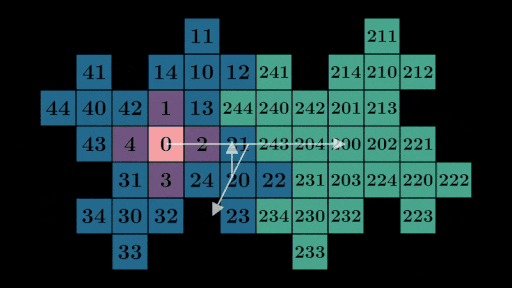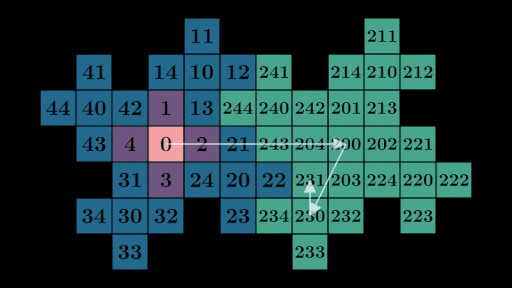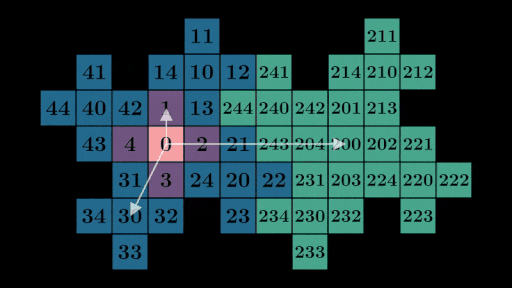
如果您取左侧的任何数字并检查右侧 5 个空格,您会发现它在青色花瓣上的副本。比较单元格之间的数字,它们似乎总是原始值加上 200。例如,44 右侧 5 个空格,您会找到 244,而 3 右侧 5 个空格是 203。在某种意义上,加上 200 似乎编码了“向右移动”5 个空格。这种“移动”属性并非 200 独有:考虑 0、1、2、3 和 4 相对于 30、31、32、33 和 34 的位置。
如果您凝视足够长的时间,您可能会注意到通过展开任何数字,例如 231 = 200 + 30 + 1,我们可以使用展开形式中的每个数字来找到它在网格上的位置。在这种情况下,我们可以在网格上找到对应于 200、30 和 1 的向量并将它们加在一起以获得 231 的位置:
您可以使用将数字分解为其 1 位数、10 位数、100 位数等位置并添加向量的相同策略来测试其他数字。假设这通常有效,我们只需要知道展开形式中每个数字的位置即可找到网格上任何数字的位置,然后将它们加在一起。让我们 ~~滥用~~ 引入一些表示法,将 \(\vec{n}\) 定义为指向数字 \(n\) 在网格上的位置的向量。以我们的 1 位数值为例: \(\begin{align} \overrightarrow{0} &= \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{1} &= \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{2} &= \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{3} &= \begin{bmatrix} -1 \\ 0 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{4} &= \begin{bmatrix} 0 \\ -1 \\ \end{bmatrix} \end{align}\)
有了这种新的表示法,我们可以凝视“10 的幂”的行为方式: \(\begin{align} \overrightarrow{1} &= \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{10} &= \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{100} &= \begin{bmatrix} 0 \\ 5 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{1000} &= \begin{bmatrix} 5 \\ 10 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{10000} &= \begin{bmatrix} 0 \\ 25 \\ \end{bmatrix} \end{align},\)\(\begin{align} \overrightarrow{100000} &= \begin{bmatrix} 25 \\ 50 \\ \end{bmatrix} \end{align}\)
仔细观察,您可能会发现模式:
\[\begin{equation} \overrightarrow{(10^n)} = \begin{cases} 5^n \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix} & \text{if } n \text{ is even} \\ 5^{(n-1)} \begin{bmatrix} 1 \\ 2 \\ \end{bmatrix} & \text{if } n \text{ is odd} \end{cases} \end{equation}\]
这个条件公式是我最初编写可视化代码的方式。然而,它提出了一个问题:是否有一种更优雅的方法来计算这些值而不需要条件?理想情况下,我们想要一种可以根据 \(n\) 的值重复应用以缩放和旋转向量的变换,即矩阵的 \(n\) 次幂。经过一番摸索,我们可以找到矩阵 \(M\) 及其幂:
\(M = \begin{bmatrix} -2 & 1 \\ 1 & 2\\ \end{bmatrix},\)\(M^2 = \begin{bmatrix} 5 & 0 \\ 0 & 5\\ \end{bmatrix},\)\(M^3 = \begin{bmatrix} -10 & 5 \\ 5 & 10\\ \end{bmatrix},\)\(M^4 = \begin{bmatrix} 25 & 0 \\ 0 & 25\\ \end{bmatrix}, \text{etc...}\)
这方便地匹配了我们期望的值,而无需 在等式中使用条件:
\[\overrightarrow{(10^n)} = M^n\overrightarrow{1} = \begin{bmatrix} -2 & 1 \\ 1 & 2\\ \end{bmatrix}^n\begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}\]
同样,我们可以为其他可能的数字设置方程式:
\[\begin{align} \overrightarrow{(2 \cdot 10^n)} &= M^n\overrightarrow{2} = \begin{bmatrix} -2 & 1 \\ 1 & 2\\ \end{bmatrix}^n\begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} \newline \overrightarrow{(3 \cdot 10^n)} &= M^n\overrightarrow{3} = \begin{bmatrix} -2 & 1 \\ 1 & 2\\ \end{bmatrix}^n\begin{bmatrix} 0 \\ -1 \\ \end{bmatrix} \newline \overrightarrow{(4 \cdot 10^n)} &= M^n\overrightarrow{4} = \begin{bmatrix} -2 & 1 \\ 1 & 2\\ \end{bmatrix}^n\begin{bmatrix} -1 \\ 0 \\ \end{bmatrix} \end{align}\]
如果你因为诅咒的符号而流泪而模糊了双眼,你可能会发现它与以 5 为基数或以 10 为基数等数字系统的联系。类似于以 10 为基数时,数字 1234 将展开为:
\[\begin{aligned} 1234 &= 10^3 \cdot 1 + 10^2 \cdot 2 + 10^1 \cdot 3 + 10^0 \cdot 4 \newline 1234 &= 1000 + 200 + 30 + 4 \end{aligned}\]
以 5 为基数时:
\[\begin{aligned} 1234_5 &= 5^3 \cdot 1 + 5^2 \cdot 2 + 5^1 \cdot 3 + 5^0 \cdot 4 \newline 1234_5 &= 1000_5 + 200_5 + 30_5 + 4_5 \end{aligned}\]
我们可以使用矩阵 \(M\) 作为我们的基,并使用向量作为我们的数字来编码分形中的位置:
\[\begin{aligned} \overrightarrow{1234} &= M^3\overrightarrow{1} + M^2\overrightarrow{2} + M^1\overrightarrow{3} + M^0\overrightarrow{4} \newline \overrightarrow{1234} &= \overrightarrow{1000} + \overrightarrow{200} + \overrightarrow{30} + \overrightarrow{4} \end{aligned}\]
我们偶然发现了一个具有矩阵基和向量数字的数字系统,而不是标量!从 0 开始计数,我们可以感受到数字系统如何连接到分形的结构:
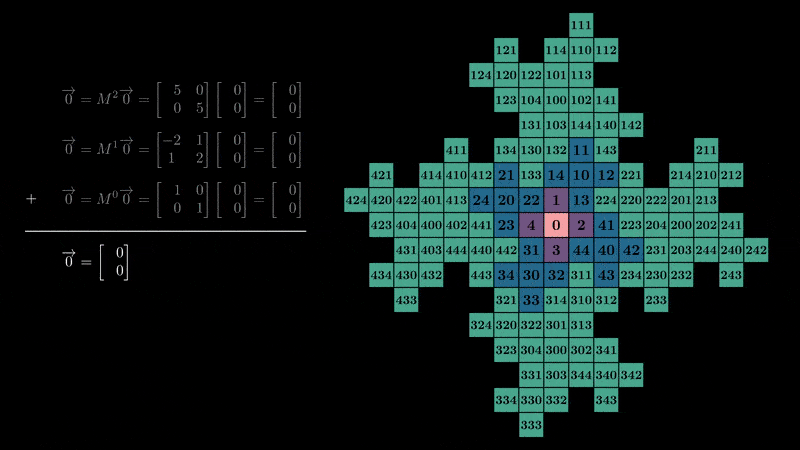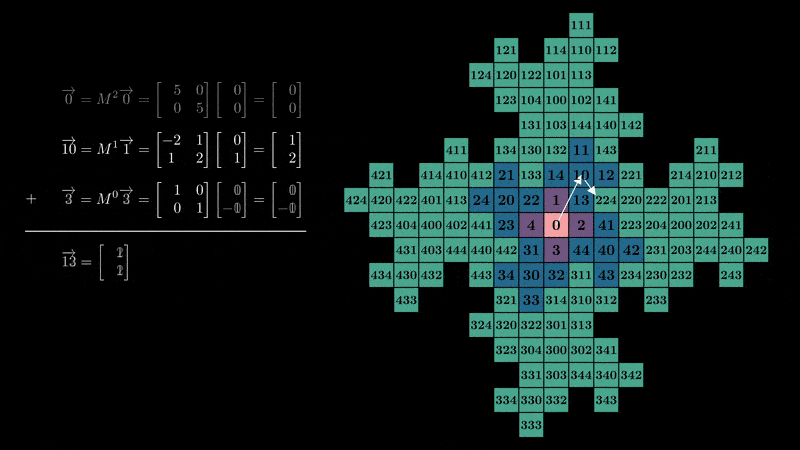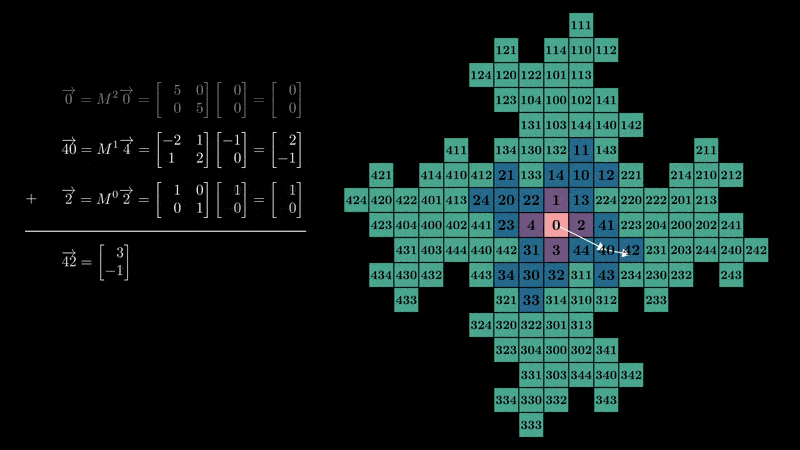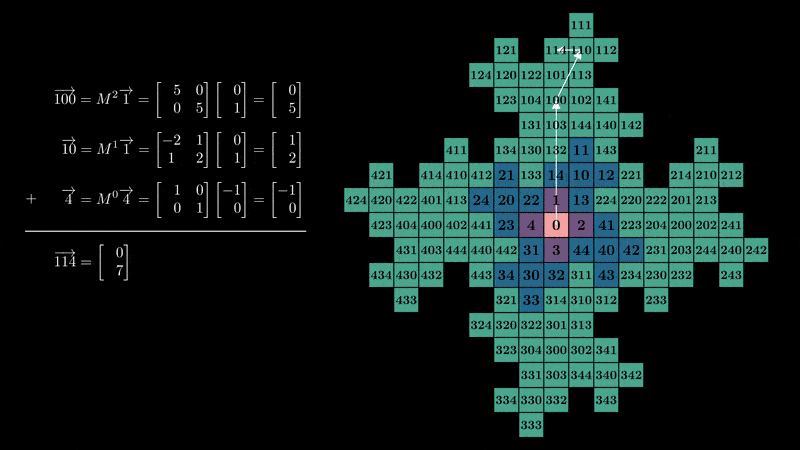
行列式
您可能已经注意到 \(20\) 和 \(40\) 与我们原始的编号相比切换了位置。这是因为我们选择的 \(M\) 具有负行列式 \(\det(M) = -5\),这意味着它具有在每次迭代中“翻转”空间方向的副作用。现在我们知道我们的分形与线性代数相关联,我们可以通过叠加缩放的网格来可视化连接,这些网格表示 \(M\) 的幂如何作用于我们的“数字向量”\(\vec{1}\)、\(\vec{2}\)、\(\vec{3}\) 和 \(\vec{4}\),如 3Blue1Brown 中所示。
为了避免翻转行为,我们需要选择一个具有正行列式的矩阵,例如:
\[M^\prime = \begin{bmatrix} 2 & 1 \\ -1 & 2\\ \end{bmatrix}\] \[\det(M^\prime) = 5\]
可视化这种新的矩阵选择:
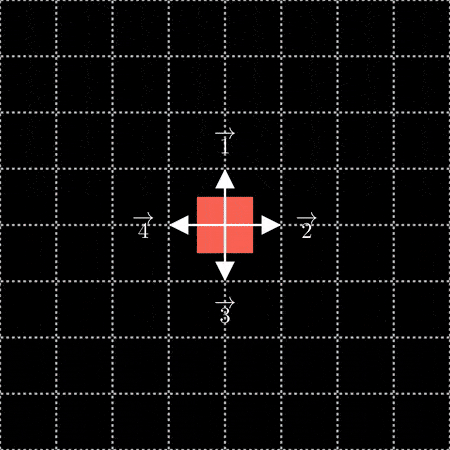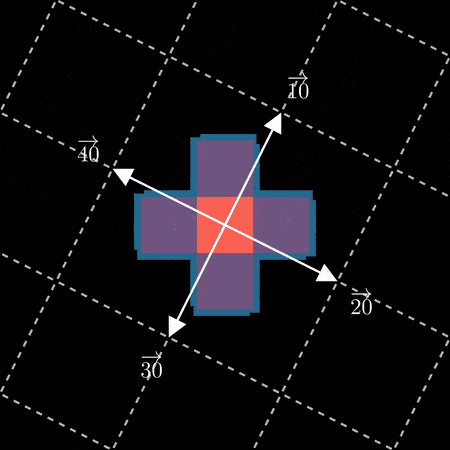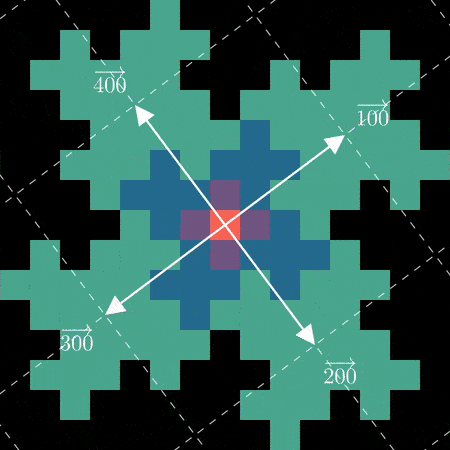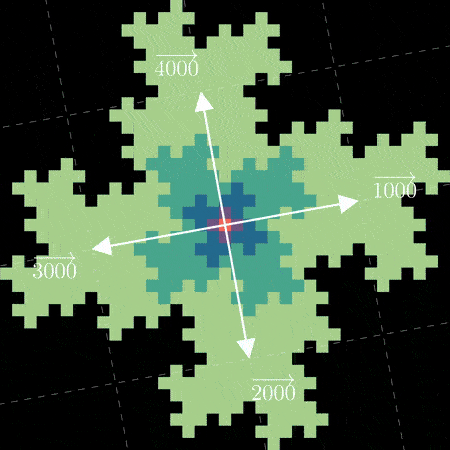
这种基的选择不是每隔一次迭代就“翻转”并与轴重新对齐,而是不断顺时针旋转我们的“数字向量”。等等,我们不是在一开始就用 L-System 看到过一个这样的分形版本吗?当然,使用 \(M^\prime\) 作为我们的基会重现 L-System 版本。
谜团解开了!这两个分形 几乎 相同,但我墙上的那个是使用 \(M\) 生成的,其中 \(\det(M) = -5\),而更常见的分形是从 \(M^\prime\) 生成的,其中 \(\det(M^\prime) = 5\)。矩阵的选择也揭示了看似任意的“大约 27 度”来自哪里。您可能已经注意到两个行列式的绝对值都是 \(5\),这方便地匹配了分形每次迭代都按 5 的因子增大的方式。如果我们选择一个具有更大行列式的矩阵,我们的“数字向量”会增长得太快,并在每次迭代中留下“空空间”。例如,调整 \(M\) 使其行列式为 \(-6\) 会导致:
同时,如果我们选择一个具有较小行列式的矩阵,我们的“数字向量”会增长得太慢,并且迭代会重叠。调整 \(M\) 使其行列式为 \(-4\):

因此,表面上我们想要一个行列式为 \(\pm 5\) 的矩阵基。此外,我们希望我们的矩阵具有整数条目,以确保它始终将我们的数字向量映射到整数坐标。恰好向量 \(\left\langle 1, 2 \right\rangle\) 具有整数条目并且大小为 \(\sqrt{5}\),这意味着我们可以使用它及其 90 度旋转之一作为我们矩阵的列来满足行列式和整数约束。计算该向量的角度,我们得到 \(\arctan{\frac{2}{1}} \approx 63.43^\circ\),即偏离 y 轴“大约 27 度”。
如何加法,第二部分
您可能已经注意到向量加法在大多数情况下都会惨败,除了展开形式的情况,例如 \(\vec{2} + \vec{2} \neq \vec{4}\)。这是预料之中的,因为选择 \(2\) 和 \(4\) 是为了帮助建立与以 5 为基数的数字系统的联系,但与向量指向的实际方向无关。将 1 到 4 称为上 (\(\vec{1}\))、右 (\(\vec{2}\))、下 (\(\vec{3}\)) 和左 (\(\vec{4}\)) 可能更合适。正如您可能期望的那样,相反的方向会相互抵消,即 \(\vec{1} + \vec{3} = \vec{2} + \vec{4} = \vec{0}\)。但是其他加法组合呢?通过仔细查看以 5 为基数的编号并跟踪单位向量的组合指向的位置:
我们可以根据单位向量的总和似乎会落到的位置来构建一个表格: \(+\) | \(\overrightarrow{0}\hspace{5pt}\) | \(\overrightarrow{1}\hspace{5pt}\) | \(\overrightarrow{2}\hspace{5pt}\) | \(\overrightarrow{3}\hspace{5pt}\) | \(\overrightarrow{4}\hspace{5pt}\) ---|---|---|---|---|--- \(\overrightarrow{0}\hspace{5pt}\) | \(\overrightarrow{0}\) | \(\overrightarrow{1}\) | \(\overrightarrow{2}\) | \(\overrightarrow{3}\) | \(\overrightarrow{4}\) \(\overrightarrow{1}\hspace{5pt}\) | \(\overrightarrow{1}\) | \(\overrightarrow{14}\) | \(\overrightarrow{13}\) | \(\overrightarrow{0}\) | \(\overrightarrow{22}\) \(\overrightarrow{2}\hspace{5pt}\) | \(\overrightarrow{2}\) | \(\overrightarrow{13}\) | \(\overrightarrow{41}\) | \(\overrightarrow{44}\) | \(\overrightarrow{0}\) \(\overrightarrow{3}\hspace{5pt}\) | \(\overrightarrow{3}\) | \(\overrightarrow{0}\) | \(\overrightarrow{44}\) | \(\overrightarrow{32}\) | \(\overrightarrow{31}\) \(\overrightarrow{4}\hspace{5pt}\) | \(\overrightarrow{4}\) | \(\overrightarrow{22}\) | \(\overrightarrow{0}\) | \(\overrightarrow{31}\) | \(\overrightarrow{23}\)
该表在对角线上对称,这意味着加法是可交换的,这对于向量加法来说是预期的。更重要的是,几个加法会导致 2 位数值。虽然这可能看起来没什么大不了的,但这意味着在进行更大的加法时,我们必须担心将值结转到下一位。例如,如果我们想找到 22 正上方的数字,我们可以计算 \(\overrightarrow{22} + \overrightarrow{1}\)。使用传统的长加法和结转表示法: \[\begin{array}{cccc} & \overset{1}{\vphantom{0}} & \overset{1}{2} & 2 \\ + & & & 1 \\ \hline & 1 & 3 & 3 \\ \end{array}\] 如果您有点困惑,请记住 \(\overrightarrow{2} + \overrightarrow{1} = \overrightarrow{13}\)。如果您惊讶于这完全可行,请加入俱乐部!由于这是一篇博客文章而不是证明,我将检查这个加法方案是否普遍有效的任务留给读者。
中场休息:相关主题
由于 Balanced Ternary 使用 \(-1\)、\(0\) 和 \(1\) 作为数字,并以 \(3\) 为基数,因此在数字系统中使用 \(\mathbb{N}\) 之外的事物的概念并非完全陌生。如果您想象平衡三进制沿 x 轴是一维的,那么可以通过添加两个新的数字来考虑 wallflower 作为其二维模拟,以考虑 y 轴的正向和负向。已经存在 generalized balanced ternary 的替代方案,并使用 permutahedrons 的晶格推广到任何维度(至少从我能够挖掘到的信息来看)。在二维中,这最终成为六边形晶格:
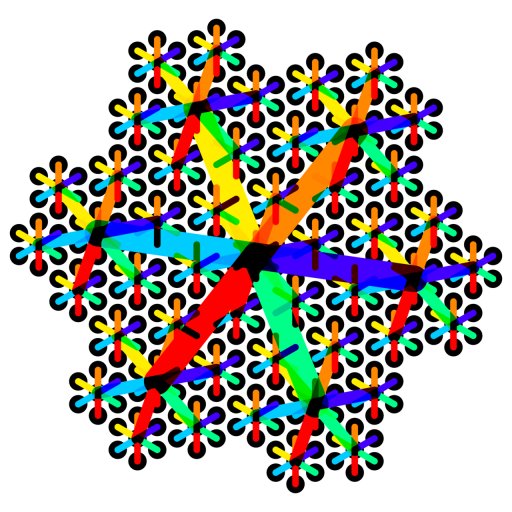 来自 Wikipedia 的使用六边形的二维广义平衡三进制的可视化。另请参见 Gosper Curve,它就像一个六边形的墙花。
另一个奇异的数字系统是 Quater-imaginary Base,它使用虚数值 \(2i\) 作为其基,并使用 \(0\)、\(1\)、\(2\) 和 \(3\) 作为数字。如果您将复数想象为向量,并将 \(2i\) 想象为执行缩放和旋转的矩阵,我们可以将此数字系统转换为我们的诅咒表示法:
\(M_{2i} = \begin{bmatrix} 0 & -2 \\ 2 & 0\\ \end{bmatrix},\)\(\overrightarrow{0} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{1} = \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{2} = \begin{bmatrix} 2 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{3} = \begin{bmatrix} 3 \\ 0 \\ \end{bmatrix}\)
来自 Wikipedia 的使用六边形的二维广义平衡三进制的可视化。另请参见 Gosper Curve,它就像一个六边形的墙花。
另一个奇异的数字系统是 Quater-imaginary Base,它使用虚数值 \(2i\) 作为其基,并使用 \(0\)、\(1\)、\(2\) 和 \(3\) 作为数字。如果您将复数想象为向量,并将 \(2i\) 想象为执行缩放和旋转的矩阵,我们可以将此数字系统转换为我们的诅咒表示法:
\(M_{2i} = \begin{bmatrix} 0 & -2 \\ 2 & 0\\ \end{bmatrix},\)\(\overrightarrow{0} = \begin{bmatrix} 0 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{1} = \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{2} = \begin{bmatrix} 2 \\ 0 \\ \end{bmatrix},\)\(\overrightarrow{3} = \begin{bmatrix} 3 \\ 0 \\ \end{bmatrix}\)
或者,我们可以将之前的正行列式矩阵 \(M^\prime\) 转换为其复数等效项,以获得一个基数为 \(2+i\) 的数字系统。Timothy James McKenzie Makarios 的 Balanced base 2+i (and some gratuitous fractals) 探讨了这个概念。我在 Google 图片上寻找四分之一虚数基的可视化效果时遇到了这个问题,结果发现早在 2016 年就已经建立了这种联系。令人尴尬的是,我在制作了开头的动画后才发现这一点,结果发现作者也已经抢在我前面了,尽管使用的是分形的 \(M^\prime\) 版本而不是 \(M\)(据我所知,\(M\) 不能编码为复数)。
当我意识到矩阵基数数字系统完全有效时,我开始四处搜索,看看是否还有其他人建立了分形、镶嵌、线性代数和数字系统之间的联系。挖掘:
- Attila Kovács 领导的 Project BinSys 专注于寻找行列式为 2 的矩阵基,用于二元数的广义形式。
- Andrew Vince 的 Replicating Tesselations 进行了所有严格的数学运算,以形式化我一直试图通过大力挥手描述的内容,并推广到任何晶格,而不仅仅是 \(\mathbb{Z}^2\)。
- 在这里您还可以找到将平衡三进制推广到更高维度的替代方法的证明。
说到挥手:下一节现在完全属于“我开始思考一周前的事情,什么时候开始写这个”,因此来自多年思考问题的任何严谨性都消失了。相反,我将依靠我对线性代数的心理模型,即“如果听起来是真的并且看起来是真的,那么它可能就是真的”。
更进一步超越
中学时的我非常喜欢 Minecraft,所以很自然地我一直想知道:分形是否适用于立方体?具体来说,是否有一种通过从立方体开始并向外复制成六个一组来形成“3D 加号”来创建分形的 3D 版本的方法?这主要归结为我们希望在推广到 3x3 矩阵时包含哪些属性。以太坊召唤我的那些是:
- 矩阵中的所有条目都必须是整数。这是必需的,因此当我们应用矩阵基数到我们的向量数字(位于轴上的 6 个单位向量)时,它们仍然具有每个分量的整数值。在 Vince 论文中,这被形式化为“\(\Lambda\) 的内同态”,即从晶格 \(\Lambda = \mathbb{Z}^3\) 到自身的映射。
- 矩阵中的每个列向量与原点的 Hamming 距离应为 3。此约束确保我们在第二次迭代中创建的“3D 加号”的 6 个副本不会与以原点为中心的原始加号重叠,但距离足够近,仍然与其相邻。
- 我们想要一个行列式为 \(\pm\)7 的矩阵。由于分形的每次迭代都添加 6 个新副本,因此我们每次都将分形的大小增加 7 倍。如果我们想有效地“打包”这些副本,我们需要确保我们应用的矩阵也将输入放大 7 倍。
通过蛮力搜索具有 Hamming 距离为 3 的向量三元组,我们得到了这个漂亮的 3x3 矩阵,它检查了所有条件:
\[\begin{bmatrix} 2 & -1 & 0 \\ -1 & 0 & 2 \\ 0 & -2 & 1 \\ \end{bmatrix}\]
可视化给了我们:
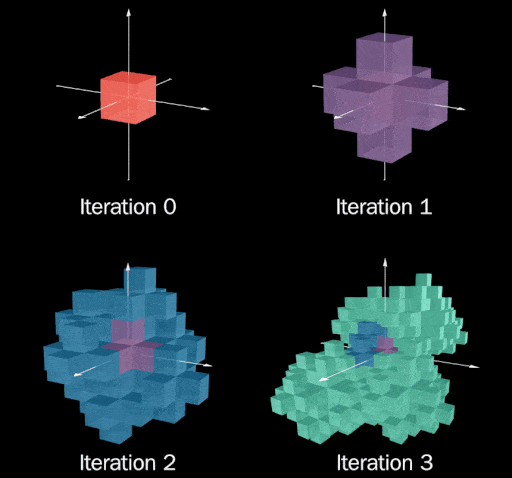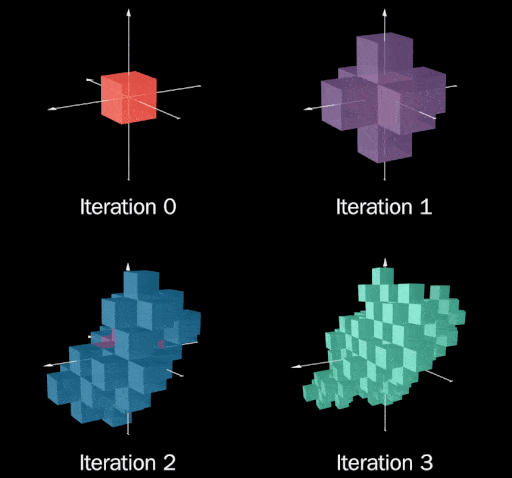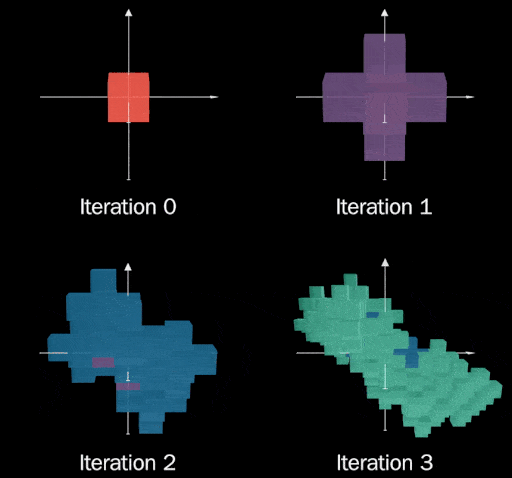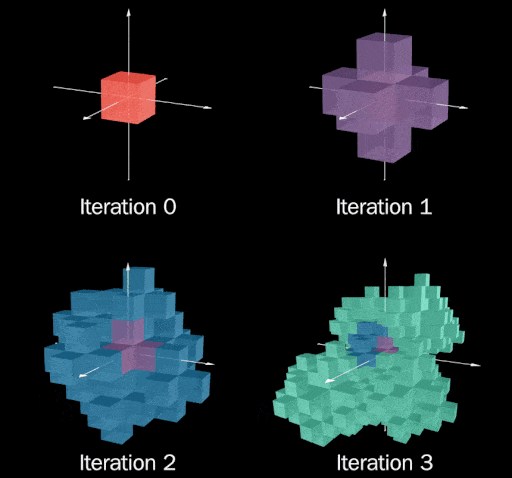
哇,看起来糟透了!一个立即突出的问题是,后来的迭代似乎被“压扁”了,导致先前迭代暴露出来的斑点。仔细观察迭代 2,您可能会注意到我们可以通过在 \(\left\langle 1, 1, 1\right\rangle\) 和 \(\left\langle-1, -1, -1\right\rangle\) 上添加两个“3D 加号”来梳
