main page / research / cv / github

如何通过灌铅骰子在《卡坦岛拓荒者》中作弊 (并用 p-value 证明)

发表于 2017-12-14

tl;dr 这篇文章展示了如何制作灌铅骰子，以及如何使用这些骰子在每局《Settlers of Catan》游戏中获得额外的 5-15 张资源卡。 令人惊讶的是，我们将证明标准的科学测试不足以确定骰子是否不公平。 这实际上意味着你的对手不可能科学地证明你在作弊。 这种不可能源于当前科学实践中的方法论缺陷，我们将重点介绍一些正在进行的工作来解决这些缺陷。

灌铅骰子

我的《Settlers of Catan》游戏配有两个普通的木制骰子。为了给这些骰子灌铅，我把它们放在一小盘水中过夜，使 6 的一面朝上。

浸没的区域吸收了水分，变得更重。 我希望掷骰子时，较重的湿面更有可能面朝下，而较轻的干面更有可能面朝上。 因此，通过将 6 暴露在外，我希望制造出更经常掷出 6 的骰子。

这种效应被称为骰子的 bias（偏差）。 为了测量这种偏差，我和我的妻子在接下来的 7 天里，一边吃晚饭一边掷骰子。（她一定非常爱我！）

总共，我们掷了 4310 次骰子。 原始结果如下所示。

1 | 2 | 3 | 4 | 5 | 6 ---|---|---|---|---|--- number of rolls (掷骰次数) | 622 | 698 | 650 | 684 | 666 | 812 probability (概率) | 0.151 | 0.169 | 0.157 | 0.165 | 0.161 | 0.196

查看数据，“显而易见”我们的骰子是有偏差的：6 被掷出的次数比任何其他数字都多。 然而，在我们正式证明这种偏差之前，让我们设计一个策略，在玩《Settlers of Catan》时利用这种偏差。

灌铅骰子的策略

在《Settlers of Catan》中获胜的关键是获得大量资源。 我们想知道使用我们有偏差的骰子可以获得多少额外资源。

首先，让我们快速回顾一下规则。 每个定居点都放置在三个地块的角落，每个地块都有一个数字标记。 每次掷骰子时，如果它们加起来等于标记上的数字之一，你就会收集相应的资源卡。 例如：

一个好的定居点将放置在经常掷出的数字旁边。

为了使制定策略更容易，游戏设计师在每个数字标记的下方都放置了有用的点。 这些点计算了使用两个骰子掷出该标记数字的方式。

我们可以使用这些点来计算掷出每个数字的概率。 例如，4 可以通过三种方式掷出。 如果我们命名我们的两个骰子为 A 和 B，那么可能的组合是 (A=1,B=3), (A=2,B=2), (A=3,B=1)。 为了计算掷出 4 的概率，我们计算每个掷出的概率并将它们加在一起。 对于公平的骰子，每个掷出的概率是相同的 (1/6)，因此计算公式为：

Pr(A+B=4)=Pr(A=1)Pr(B=3)+Pr(A=2)Pr(B=2)+Pr(A=3)Pr(B=1)=(1/6)(1/6)+(1/6)(1/6)+(1/6)(1/6)=1/12≈0.08333

对于我们有偏差的骰子，每个掷出的概率是不同的。 使用上表中的数字，我们得到：

Pr(A+B=4)=Pr(A=1)Pr(B=3)+Pr(A=2)Pr(B=2)+Pr(A=3)Pr(B=1)=(0.151)(0.157)+(0.169)(0.169)+(0.157)(0.151)=0.07597

因此，使用我们有偏差的骰子掷出 4 的可能性现在较小。 对每个可能的数字执行此计算，我们得到以下图表。

所有小于 7 的数字现在可能性较小，而大于 7 的数字现在可能性更大。 这种变化很小，但具有重要的战略意义。

考虑以下两个初始定居点位置。

狡猾的玩家知道骰子是有偏差的，并将她的定居点放在数字高的位置，但友好的玩家不知道骰子是有偏差的，并将她的定居点放在数字低的位置。 请注意，如果骰子是公平的，那么两个定居点位置同样好，因为它们具有相同数量的点。

以下公式计算玩家每次掷骰子获得的平均卡牌数量：

expected cards per roll (每次掷骰子期望获得的卡牌数量)=∑adjacent tokensPr(A+B=token value)

替换适当的值，我们得到以下结果。

expected cards per roll (每次掷骰子期望获得的卡牌数量)

naughty (狡猾的玩家) | nice (友好的玩家) fair dice (公平的骰子) | 0.500 | 0.500 biased dice (有偏差的骰子) | 0.543 | 0.457

因此，狡猾的玩家和友好的玩家之间的差异是每次掷有偏差的骰子 0.086 张卡牌。 一个典型的《Settlers》游戏包含大约 60 次掷骰子（在 4 人游戏中，每位玩家大约 15 轮），因此这会导致狡猾的玩家多获得 0.086*60=5.16 张卡牌。

而这仅仅考虑了两个起始定居点。 随着游戏的进行，将建造更多的定居点，一些定居点将升级为城市（每次掷骰子收到两张卡牌而不是一张）。 计算这些额外卡牌来源的确切效果很困难，因为这些改进将在整个游戏中的随机时间点建造。 我们将不得不做出一些额外的假设。

如果我们假设狡猾的玩家每次掷骰子每个定居点/城市比友好的玩家多获得 0.043 张卡牌（这个确切的数字会因定居点的质量而异），并且两个玩家都在第 10,20,25,30,35,40,45 和 50 回合建造定居点/城市，那么狡猾的玩家平均将比友好的玩家多获得 15.050 张卡牌。

总而言之，狡猾的玩家将收到大约 5 到 15 张额外的资源卡，具体取决于他们未来的定居点和城市的建造方式。 这种优势不能保证胜利，但肯定会有所帮助。

科学分析

现在我们将进行一些简单的统计来证明两件事：

  1. 骰子确实是有偏差的。 因此，6 被掷出的次数比其他数字多的事实并非仅仅是由于随机机会造成的。
  2. 在《Settlers》游戏中掷骰子的次数不足以让我们的对手科学地证明骰子是有偏差的。 因此，我们的对手在科学上不可能知道我们在作弊。

为了表明骰子是有偏差的，我们将使用一种称为null hypothesis significance testing (零假设显著性检验)的标准科学技术。 我们首先假设一个我们想要 推翻 的假设。 在我们的例子中，我们假设骰子 没有 偏差。 换句话说，我们假设骰子上的每个数字都有 1/6≈0.166 的机会被掷出。 我们的目标是表明，在这种假设下，上面掷出的 6 的数量非常不可能。 因此，我们得出结论，我们的假设也不太可能，并且骰子可能实际上是有偏差的。

更正式地说，我们令 X 为一个随机变量，它表示如果我们用公平的骰子重复我们的初始实验，我们将掷出的 6 的总数。 那么 X 服从一个 binomial distribution (二项分布)，其密度绘制如下。 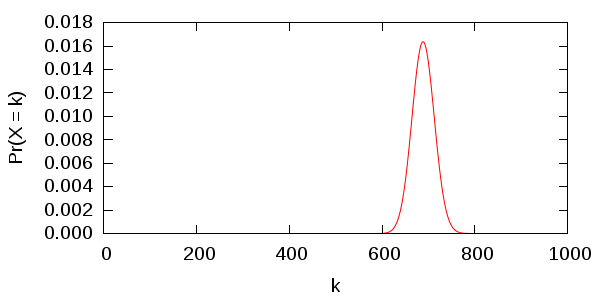我们的实验的 p-value (p 值) 被非正式地定义为，如果骰子 没有 偏差，则获得与我们观察到的结果相似的结果的概率。 正式定义和公式为 p-value=Pr(X≥k)=1−k∑i=0(nk)qi(1−q)n−i,

其中 n 是掷骰子的总次数 (4310)，k 是实际掷出的 6 的数量 (812)，q 是假设掷出 6 的概率 (1/6)。 替换这些数字，我们得到 p-value=Pr(X≥k)≈0.0000884。 换句话说，如果我们用公平的骰子重复这个实验一百万次，我们预计只会得到 88 次与我们实际得到的结果相似的结果。 由于这太不可能了，我们得出结论，我们最初的假设（即骰子没有偏差）可能是错误的。 大多数科学课程都教授 p-value 小于 0.05 是“显著的”。 我们远低于该阈值，因此我们的结果是“非常显著的”。

我们的 p-value 非常低，因为我们进行的试验次数非常多 (n=4310)。 然而，在典型的《Settlers》游戏中，试验次数会少得多。 这使得我们的对手很难证明我们在作弊。

我们之前说过，在典型的游戏中会掷骰子 60 次。 由于我们有两个骰子，这意味着 n=120。 为了使数学计算简单，我们将假设我们掷出平均数量的 6。 也就是说，游戏中掷出的 6 的数量是 k=812⋅1204310≈23。 替换到我们的 p-value 公式中，我们得到 p-value=P(X≥k)≈0.265。 换句话说，这意味着如果骰子实际上是公平的，那么我们仍然会在 26.5% 的时间内掷出这个数量的 6。 由于这个概率很高，标准的科学协议告诉我们得出结论，我们没有“显著”的证据表明骰子是有偏差的。（请注意，这与有证据表明骰子没有偏差略有不同！ 混淆这两个陈述是一个常见的错误，即使对于训练有素的博士科学家也是如此，尤其是对于医生来说。）

那么我们可以玩多少场游戏而不会被抓住？ 事实证明，如果我们玩 6 场游戏（因此 n=6*120=720，并且 k=812⋅(720/4310)≈136），那么得到的 p-value 是 0.05。 换句话说，只要我们玩少于 6 场游戏，那么我们的对手就没有足够的数据来得出结论，他们对有偏差骰子的测量是“显著的”。 标准的科学方法无法证明我们在作弊。

p-value 和“显著性”的一些缺陷

上面的 p-value 参数是大多数科学家目前测试其假设的方式。 但这种方法存在一些重大缺陷。 例如：

  1. p-value 测试没有使用所有可用的信息。 特别是，我们的对手可能有其他理由相信骰子是灌铅的。 如果你仔细观察骰子，你会注意到一些轻微的变色，因为它浸没在水中。

这种变色是由于水扩散了骰子面上的墨水造成的。 如果你在游戏中的骰子上看到类似的变色，那么对骰子的偏差保持额外的怀疑是有道理的。

不幸的是，没有办法将这种怀疑纳入我们上面进行的 p-value 分析中。 一种称为 bayes factor (贝叶斯因子)的 p-value 替代方法可以纳入这种先前的证据。 因此，如果我们的对手使用贝叶斯因子分析，他们可能能够确定我们在作弊。 然而，贝叶斯因子比 p-value 更复杂，因此它没有被广泛地教授给本科科学专业的学生。 它甚至很少在博士级别的科学出版物中使用，并且许多统计学家都在呼吁更多地使用这些更复杂的分析技术。

  1. p-value 测试的另一个弱点是 false positives (假阳性) 非常普遍。 使用 p≤0.05 的标准显著性阈值意味着每 100 场游戏中将有 5 场游戏具有“显著”的证据表明骰子有偏差，可以掷出 6。 然而，常识告诉我们，在《Settlers of Catan》中作弊几乎肯定不常见，因为大多数人只是不想作弊。 但是当你运行许多实验时，其中一些实验会仅仅通过随机机会给出“显著”的结果。 这是科学家得出结论大多数已发表的研究都是错误的的原因之一。 人们认为这种效应是 extra sensorial perception (ESP) (超感官知觉)的证据继续在科学期刊上发表的原因之一。 一些不太谨慎的科学家利用这种缺陷，通过一种称为 p-hacking (p 值操纵) 的过程来使他们的研究看起来更重要。

为了缓解假阳性的问题，一群统计学家正在提议一个新的显著性阈值 p≤0.005，以便结果符合“显著”的条件。 虽然这降低了假阳性的风险，但也使得检测真实效应变得更加困难。 在这个新标准下，我们将不得不玩 16 场游戏（对于 n=1920 次骰子掷骰）才能获得具有统计学意义的证据表明骰子是有偏差的。

此时，你可能会对统计分析的复杂性感到不知所措。 而这仅仅是为了检测游戏中灌铅骰子的玩具问题。 现实世界中的问题，例如评估化疗药物的有效性，要复杂得多，因此需要进行更复杂的统计分析。 做科学很难！

同行评审后的编辑： Vijay Lulla 发送给我以下消息：

博客提到你掷了 4310 次骰子，你所有的计算都基于它，但频率表加起来是 4312。

哇！ 看起来我搞砸了我的加法。 幸运的是，这个错误很小，不会对文章中的任何数字产生太大影响。

很多人错误地认为同行评审是其他科学家重复实验以测试结论的地方。 但事实并非如此。 同行评审的目的是让像 Vijay 这样的科学家只是对整个过程进行健全性检查，以确保发现像这样的明显错误。 可悲的是，科学中另一个常见的错误是研究人员不发布他们的数据，因此无法执行此类检查。

如果这是科学期刊上的真实出版物，我会重做所有计算。 但由于不是，我将保留这个错误以供后人参考。

编辑 2： reddit 的 /r/statistics 上有一个很好的讨论。 这个讨论提供了比我上面的讨论更细致的关于显著性检验的观点，并且一些用户指出了我可能夸大某些结论的方式。

相关帖子 (查看所有帖子)

fun (乐趣)

my collection of "ancient" hebrew scrolls (我的“古代”希伯来语卷轴收藏) All content is licensed under the creative commons attribution-sharealike. You can contact me at mike@izbicki.me for just about anything.