注解版 Kolmogorov-Arnold 网络 (KAN)

对 Kolmogorov-Arnold 网络的注解指南

作者

隶属关系

Alex Zhang (非常) 近期毕业于 Princeton University

发布日期

2024年7月1日

目录

Introduction Background and Motivation Part I - The Minimal KAN Model Architecture Part II - Model Training Part III - KAN-specific Optimizations Part IV - Applied Example Appendix Citation Footnotes References

如果 LaTeX 未加载，请刷新页面。

这篇文章类似于并深受 Annotated Transformer 的启发，但针对的是 KANs。它作为一个独立的 notebook 完全可用，并提供直观理解以及代码。大多数代码编写得易于理解，并模仿了在 PyTorch 中标准深度学习模型的结构，但某些部分（如训练循环和可视化代码）改编自 原始代码库。我们决定删除原始论文中一些被认为不重要的章节，并且还包括一些额外的工作来激发对这些模型未来研究。

原始论文的标题是 "KAN: Kolmogorov-Arnold Networks"，这篇论文的作者是：Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, 和 Max Tegmark.

Introduction

在过去的十年中，深度神经网络一直是 AI 发展的驱动力。然而，它们目前存在一些已知的问题，例如缺乏可解释性、扩展问题和数据效率低下——换句话说，虽然它们功能强大，但它们并不是完美的解决方案。

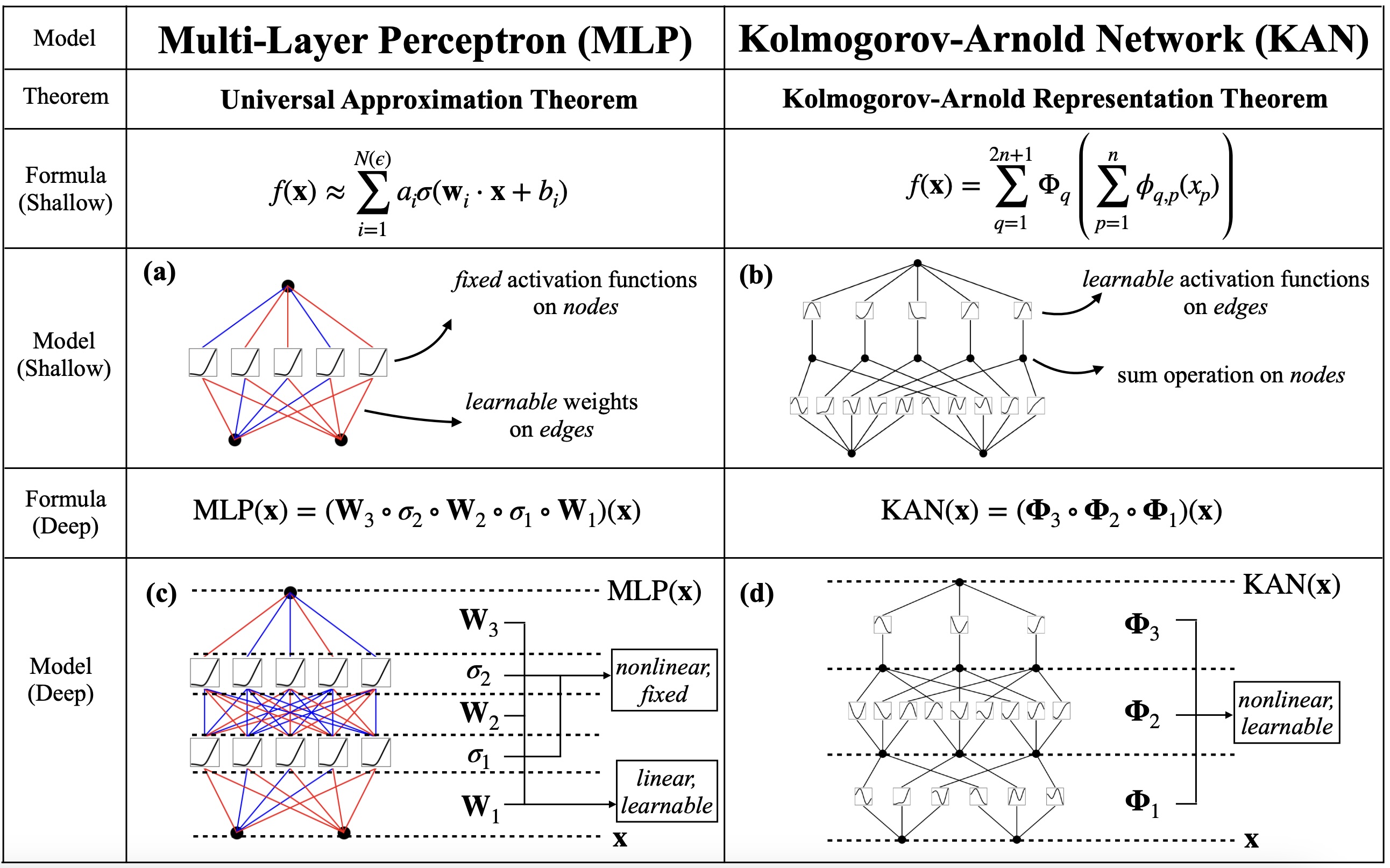从原始 KAN 论文 中截取的预告图。

Kolmogorov-Arnold 网络 (KANs) 是标准多层感知器 (MLPs) 的一种替代表示。简而言之，它们通过将 MLP 的权重矩阵-向量乘法中的“乘法”重新连接到函数应用来参数化激活函数。虽然 KANs 并没有像 MLPs 那样经过验证的成就，但它们是 AI 领域一个令人兴奋的前景，值得花一些时间进行探索。

我将这篇文章分为两个部分。第一部分和第二部分描述了一个最小的 KAN 架构和训练循环，而不强调 B-spline 优化。如果您对 KANs 感兴趣，可以使用 最小 KAN notebook。第三部分和第四部分描述了 B-spline 特定的优化和 KANs 的应用，其中包括 KAN 代码中的一些额外机制。 如果您想继续阅读，可以使用 完整的 KAN notebook。

Background and Motivation

在深入研究实现细节之前，重要的是退后一步，了解为什么人们应该关心这些模型。众所周知，多层感知器 (MLPs) 具有“通用逼近定理”，该定理为 MLP 的存在提供了一个理论保证，该定理可以近似任何函数（通常实际上并非如此）这通常不是真的。一般来说，我们对一类我们实际关心近似的函数有一些可证明的保证，例如 L1 中的函数集或平滑的连续函数集。误差高达 \(\epsilon\)。虽然这种保证很重要，但在实践中，它并没有说明通过例如随机梯度下降优化找到这样的 MLP 有多困难。

KANs 通过 Kolmogorov-Arnold 表示定理承认类似的保证，但有一个警告参见 [堆叠的 KAN 层是通用逼近器吗？] 部分。形式上，该定理指出，对于一组协变量 \((x_1,x_2,...,x_n)\)，我们可以写出任何 连续、平滑的 在这种上下文中，平滑意味着在 C^{\infty} 中，或者无限可微。 函数 \(f(x_1,...,x_n) : \mathcal{D} \rightarrow \mathbb{R}\) 在有界域 \(\mathcal{D}\) 因为它是有界的，所以作者认为我们可以将输入归一化到 [0,1]^{n} 空间，这是原始论文中假设的。形式如下 f(x_1,...,x_n) = \sum_{q=0}^{2n} \Phi_{q} \left( \sum_{p=1}^{n} \Phi_{q,p} (x_p) \right) 其中 \(\Phi_{q,p}, \Phi_{q}\) 是从 \(\mathbb{R}\) 到 \(\mathbb{R}\) 的单变量函数。理论上，我们可以通过优化类似于任何其他深度学习模型的损失函数来参数化和学习这些（可能非平滑和高度不规则的）单变量函数 \(\Phi_{q,p}, \Phi_{q}\)。但如何像参数化权重矩阵一样“参数化”一个函数，这并不是很明显。现在，假设可以参数化这些函数——原始作者选择使用 B-spline，但没有理由局限于此选择。

What is a KAN?

上述定理中的表达式并没有描述一个具有 L 层的 KAN。这是我最初感到困惑的地方。通用逼近保证仅适用于 Kolmogorov-Arnold 表示形式的模型，但目前我们没有“层”或任何可扩展概念。事实上，上述定理中的参数数量是协变量数量的函数，而不是工程师的选择！相反，作者将输入维度为 \(n\) 和输出维度为 \(m\) 的 KAN 层 \(\mathcal{K}{m,n}\) 定义为单变量函数的参数化矩阵，\(\Phi = \{\Phi{i,j}\}_{i \in [m], j \in [n]}\)。

\mathcal{K}{m,n} (\boldsymbol{x}) = \Phi \boldsymbol{x} \quad \quad \text{ where } \quad \quad \forall i \in [m], (\Phi \boldsymbol{x}){i} = \sum_{j=1}^n \Phi_{i,j} (x_j)

作者似乎凭空捏造了这个表达式，但很容易看出 KAN 表示定理可以重写如下。对于一组协变量 \(\boldsymbol{x} = (x_1,x_2,...,x_n)\)，我们可以将任何 连续、平滑的 函数 \(f(x_1,...,x_n) : \mathcal{D} \rightarrow \mathbb{R}\) 在有界域 \(\mathcal{D}\) 中写成以下形式 f(x_1,...,x_n) = \mathcal{K}{1,{2n+1}} \mathcal{K}{2n+1, n} (x_1,...,x_n)

因此，KAN 架构被写成堆叠这些 KAN 层的组合，类似于您组合 MLP 的方式。我想强调的是，除非 KAN 以以上形式书写，否则目前没有 经过验证的 我怀疑可以为深度 KAN 做出一些可证明的保证。MLP 的原始通用逼近定理指的是具有单个隐藏维度的模型，但后来的工作也推导了深度 MLP 的保证。从技术上讲，我们也没有对自我注意机制（至少据我所知）提供非常强大的可证明保证，因此我不认为这对于预测 KAN 的有用性非常重要。 存在 KAN 表示可以近似所需函数的理论保证。

Are Stacked KAN Layers a Universal Approximator?

当第一次听说 KANs 时，我的印象是 Kolmogorov-Arnold 表示定理是 KANs 的类似保证，但这似乎 并非如此。回想一下 Kolmogorov-Arnold 表示定理，我们的保证仅适用于特定的 2 层 KAN 模型。相反，作者证明存在一个使用 B-spline 作为单变量函数 \(\{\Phi_{i,j}\}_{i \in [m], j \in [n]}\) 的 KAN，它可以近似某个 不错的 误差范围内 连续可微函数的组合 这篇文章主要作为概念到代码的指南，所以我不想过多地深入研究理论。作者证明的误差范围非常奇怪，因为常数 C 并不是传统意义上的 真正的 常数（它取决于您正在近似的函数）。此外，他们选择近似的函数族似乎非常普遍，但我实际上不太确定它不能很好地表示哪些类型的函数。我建议您自己阅读定理 2.1，但它主要用于证明该论文使用 B-spline 而不是通用 KAN 网络的合理性。 。他们的主要保证被证明是为了证明使用 B-spline 作为其可学习激活的合理性，但最近也出现了其他作品，提出了不同的可学习激活，如 Chebyshev 多项式、RBFs 和小波函数 。

总结；不，我们尚未表明通用 KAN 模型可以像 MLP 一样充当通用逼近器（尚未）。

Polynomials, Splines, and B-Splines

我们广泛讨论了“可学习的激活函数”，但这个概念可能对一些读者来说并不清楚。为了参数化一个函数，我们必须定义一些使用系数的“基本”函数。在学习该函数时，我们实际上是在学习系数。原始 Kolmogorov-Arnold 表示定理对可学习的单变量激活函数的族没有提出任何条件。理想情况下，我们希望某种参数化的函数族可以近似任何函数，无论它是非平滑的、分形的还是某些其他令人讨厌的属性 在有界域上 不仅原始的 KAN 表示定理是在有界域上，而且通常在大多数实际应用中，我们处理的不是无界域上的数据。。

输入 B-spline。 B-spline 是样条函数的推广，样条函数本身是分段多项式。 \(k\) 阶/次多项式可以写成 \(p(x) = a_0 + a_1x + a_2x^2 + ... + a_kx^k\)，并且可以根据它们的系数 \(a_0,a_1,...,a_k\) 进行参数化。根据 Stone-Weierstrass 定理 ，我们可以保证有界域上的每个连续函数都可以用多项式近似。样条，以及 B-spline，将此保证扩展到有界域上的更复杂的函数。我不想分散对 KAN 的关注，因此要了解更多背景信息，我建议阅读 此资源。

B-spline 函数不是像样条那样显式地分块，而是写成以下形式的基函数的和 B(x) \triangleq \sum_{i=1}^{G} c_i B_{i,k}(x). 其中 \(G\) 表示网格点的数量，因此也表示基函数的数量（我们尚未定义），k 是 B-spline 的阶数，\(c_i\) 是可学习的参数。像样条一样，B-spline 具有一组 G 个网格点 这些也称为节点。 B-spline 由控制点确定，控制点是我们试图拟合的数据点。有时节点和控制点可能相同，但通常节点是预先固定的并且可以调整。 \((t_1,t_2,...,t_G)\)。在 KAN 论文中，他们将这些点增加到 \((t_{-k}, t_{-k+1},...,t_{G+k-1},t_{G+k})\) 以说明 B-spline 的阶数 阅读 https://web.mit.edu/hyperbook/Patrikalakis-Maekawa-Cho/node17.html 以获得更好的解释，说明为什么需要这样做。这主要是为了使基函数得到很好的定义。 给了我们一个增强的网格大小 \(G+2k\)。 网格点最简单的定义是将有界域均匀地分成 G 个等间距的点——从我们对基函数的定义中，您将看到增强的点只需要位于端点。 Cox-de Boor 公式递归地描述了这些基函数如下： \begin{aligned} B_{i,0}(x) &\triangleq \mathbf{1}{\{x \geq t_i\}} * \mathbf{1}{\{x < t_{i+1}\}} \\ B_{i, j}(x) &\triangleq \frac{x - t_i}{t_{i+j} - t_i} B_{i,j-1}(x) + \frac{t_{i+j+1} - x}{t_{i+j+1} - t_{i+1}} B_{i+1,j-1}(x) \end{aligned} 我们可以绘制一个示例，其中 B-spline 的基函数具有 G=5 个网格点，阶数为 k=3。换句话说，增强的网格大小为 G+2k=11：

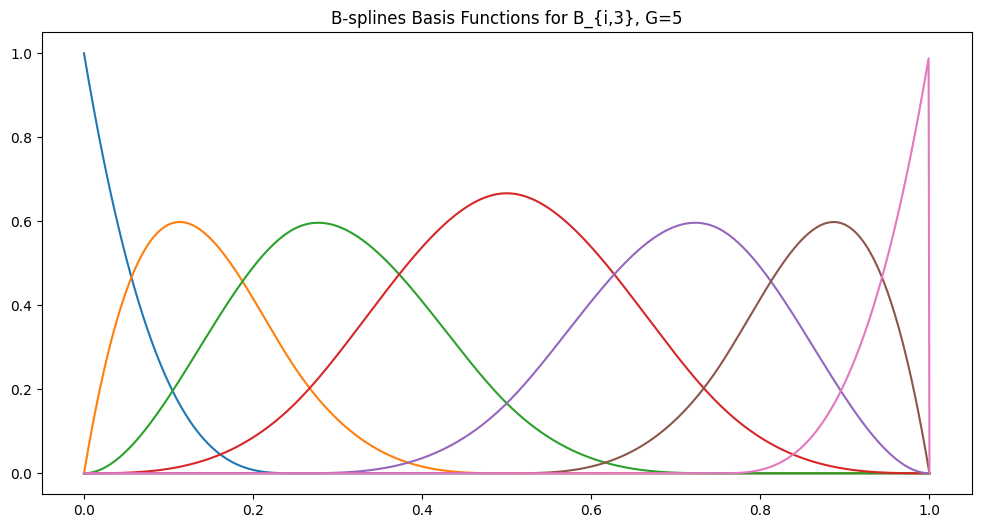B-spline 基函数的 Matplotlib 图。值得注意的是，基函数（如样条多项式）在域的大部分区域上为 0。但与样条不同，它们是重叠的。我通过改编来自 https://github.com/johntfoster/bspline/ 的代码生成了此图。

在为我们的 KAN 实现 B-spline 时，我们对函数 \(f(\cdot)\) 本身不感兴趣，而是关心有效地计算在点 \(f(x)\) 处评估的函数。稍后我们将看到 Cox-de Boor 递归的不错的迭代自下而上的动态编程公式。

Part I: The Minimal KAN Model Architecture

在本节中，我们将描述一个简陋的、最小的 KAN 模型。目标是表明该架构的结构与读者过去最可能见过的深度学习代码非常相似。为了总结这些组件，我们将我们的代码模块化为 (1) 高级 KAN 模块，(2) KAN 层，(3) 参数初始化方案，和 (4) 用于解释模型激活的绘图函数。

Preliminaries

如果您使用的是 Colab，则可以像代码块一样运行以下代码。此实现对 GPU 非常不友好，因此 CPU 就足够了。

# 代码是用 Python 3.11.9 编写的，但大多数可用的 Python 和 torch 版本都足够。
!pip install torch==2.3.1
!pip install numpy==1.26.4
!pip install matplotlib==3.9.0
!pip install tqdm==4.66.4
!pip install torchvision==0.18.1

为了使此代码简陋，我尝试尽可能少地使用依赖项。我还包括了代码的类型注释。

# Python libraries
import os
from typing import List, Dict, Optional, Self
import random
import warnings

# Installed libraries
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

以下配置文件保存了论文中描述的一些预设超参数。大多数这些都可以更改，甚至可能不适用于更通用的 KAN 架构。

class KANConfig:
    """
    Configuration struct to define a standard KAN.
    """
    residual_std = 0.1
    grid_size = 5
    spline_order = 3
    grid_range = [-1.0, 1.0]
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

The KAN Architecture Skeleton

如果您了解 MLP 的工作原理，那么以下架构应该看起来很熟悉。与往常一样，给定一组输入特征 \((x_1,...,x_n)\) 和所需的输出 \((y_1,...,y_m)\)，我们可以将我们的 KAN 视为由权重 \(\theta\) 参数化的函数 \(f : \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}\)。与任何其他深度学习模型一样，我们可以按层方式分解 KAN，并将计算细节卸载到层类。我们将根据整数列表 layer_widths 完全描述我们的模型，其中第一个数字表示输入维度 \(n\)，最后一个数字表示输出维度 \(m\)。

class KAN(nn.Module):
    """
    Standard architecture for Kolmogorov-Arnold Networks described in the original paper.
    Layers are defined via a list of layer widths. This minimal implementation doesn't include
    optimizations used specifically for B-splines.
    """
    def __init__(
        self,
        layer_widths: List[int],
        config: KANConfig,
    ):
        super(KAN, self).__init__()
        self.layers = torch.nn.ModuleList()
        self.layer_widths = layer_widths
        # If layer_widths is [2,4,5,1], the layer
        # inputs are [2,4,5] and the outputs are [4,5,1]
        in_widths = layer_widths[:-1]
        out_widths = layer_widths[1:]
        for in_dim, out_dim in zip(in_widths, out_widths):
            self.layers.append(
                KANLayer(
                    in_dim=in_dim,
                    out_dim=out_dim,
                    grid_size=config.grid_size,
                    spline_order=config.spline_order,
                    device=config.device,
                    residual_std=config.residual_std,
                    grid_range=config.grid_range,
                )
            )

    def forward(self, x: torch.Tensor):
        """
        Standard forward pass sequentially across each layer.
        """
        for layer in self.layers:
            x = layer(x)
        return x

The KAN Representation Layer

每层使用的表示形式非常直观。对于输入 \(x \in \mathbb{R}^{n}\)，我们可以将输出维度为 \(m\) 的标准 MLP 层与等效的 KAN 层直接进行比较： \begin{aligned} h_{MLP} = \sigma (W \boldsymbol{x} + b) \quad \quad &\text{ where } \quad \quad \forall i \in [m], (W\boldsymbol{x}){i} = \sum{k=1}^n W_{i,k} x_k \
h_{KAN} = \Phi \boldsymbol{x} + b \quad \quad &\text{ where } \quad \quad \forall i \in [m], (\Phi \boldsymbol{x}){i} = \sum{k=1}^n \Phi_{i,k} (x_k) \end{aligned}

换句话说，这两个层都可以用广义矩阵-向量运算来编写，其中对于 MLP，它是标量乘法，而对于 KAN，它是某些 可学习的 非线性函数 \(\Phi_{i,k}\)。有趣的是，这两个层看起来非常相似！ 注：作为一名 GPU 爱好者，我应该提到，虽然这两个表达式看起来非常相似，但这种细微的差异会对效率产生巨大影响。将相同的指令（例如乘法）应用于每个操作非常适合用于编写 CUDA 内核的 warp 抽象，而每个操作应用不同的函数会产生许多问题，例如控制发散，从而显着降低性能。

让我们考虑一下我们将如何执行此计算。为了进行分析，我们将忽略批处理维度，因为通常这是一个简单的扩展。假设我们有一个输入维度为 \(n\) 和输出维度为 \(m\) 的 KAN 层 \(\mathcal{K}_{m,n}\)。正如我们之前讨论的那样，对于输入 \((x_1,x_2,...,x_n)\)，

\mathcal{K}{m,n}(x_1,x_2,...,x_n) \triangleq \left(\sum{k=1}^n \Phi_{1,k} (x_k), \sum_{k=1}^n \Phi_{2,k} (x_k),...,\sum_{k=1}^n \Phi_{m,k} (x_k) \right)

以矩阵形式，这可以很好地写成

\begin{bmatrix} \Phi_{1,1} (\cdot) & \Phi_{1,2} (\cdot) & ... & \Phi_{1,n} (\cdot)\
\Phi_{2,1} (\cdot) & \Phi_{2,2} (\cdot) & ... & \Phi_{2,n} (\cdot) \
\vdots & \vdots & ... & \vdots \
\Phi_{m,1} (\cdot) & \Phi_{m,2} (\cdot) & ... & \Phi_{m,n} (\cdot) \
\end{bmatrix} \begin{bmatrix} x_1 \
x_2 \
\vdots \
x_n \end{bmatrix} = \begin{bmatrix} \Phi_{1,1}(x_1) + \Phi_{1,2}(x_2) + ... + \Phi_{1,n}(x_n) \
\Phi_{2,1}(x_1) + \Phi_{2,2}(x_2) + ... + \Phi_{2,n}(x_n) \
\vdots \
\Phi_{m,1}(x_1) + \Phi_{m,2}(x_2) + ... + \Phi_{m,n}(x_n) \
\end{bmatrix}

细心的读者可能会注意到，这看起来与 MLP 中使用的 Wx 矩阵完全一样。换句话说，我们必须计算并实现 为了方便起见，我们将立即实现下面的值矩阵。我怀疑，与矩阵乘法类似，可能有一种方法可以避免立即实现完整的矩阵，但这需要巧妙地选择 \Phi 的函数族。 下面矩阵中的每个项，然后沿行求和。

\text{The terms we need to compute are } \begin{bmatrix} \Phi_{1,1}(x_1), \Phi_{1,2}(x_2), ..., \Phi_{1,n}(x_n) \
\Phi_{2,1}(x_1), \Phi_{2,2}(x_2), ...,\Phi_{2,n}(x_n) \
\vdots \
\Phi_{m,1}(x_1), \Phi_{m,2}(x_2), ..., \Phi_{m,n}(x_n) \
\end{bmatrix}

为了完成抽象 KAN 层（记住，我们还没有定义什么是可学习的激活函数），作者将每个可学习的激活函数 \Phi_{i,j}(\cdot) 定义为可学习的激活函数 s_{i,j}(\cdot) 的函数，以在网络中添加残差连接：

\begin{aligned} \Phi_{i,j}(x) &\triangleq w^{(b)}{i,j} \cdot \text{SiLU}(x) + w^{(s)}{i,j} \cdot s_{i,j}(x) \quad \quad \forall i \in [m], j \in [n] \
\text{SiLU}(x) &\triangleq \frac{x}{1 + e^{-x}} \end{aligned}

我们可以将上面的操作模块化为一个“加权残差层”，该层作用于 \((\text{out_dim}, \text{in_dim})\) 值的矩阵。该层由每个 \(w^{(b)}{i,j}\) 和 \(w^{(s)}{i,j}\) 参数化，因此我们可以将 \(\boldsymbol{w}^{(b)}\) 和 \(\boldsymbol{w}^{(s)}\) 存储为参数化的权重矩阵。该论文还指定了 \(w^{(b)}{i,j} \sim \mathcal{N}(0, 0.1)\) 和 \(w^{(s)}{i,j} = 1\) 的初始化方案。对于下面的所有代码注释，我将 bsz 标注为批量大小。通常，这只是一个额外的维度，可以在分析过程中忽略。

class WeightedResidualLayer(nn.Module):
    """
    Defines the activation function used in the paper, phi(x) = w_b SiLU(x) + w_s B_spline(x) as a layer.
    """
    def __init__(
        self,
        in_dim: int,
        out_dim: int,
        residual_std: float = 0.1,
    ):
        super(WeightedResidualLayer, self).__init__()
        self.univariate_weight = torch.nn.Parameter(
            torch.Tensor(out_dim, in_dim)
        ) # w_s in paper
        # Residual activation functions
        self.residual_fn = F.silu
        self.residual_weight = torch.nn.Parameter(
            torch.Tensor(out_dim, in_dim)
        ) # w_b in paper
        self._initialization(residual_std)

    def _initialization(self, residual_std):
        """
        Initialize each parameter according to the original paper.
        """
        nn.init.normal_(self.residual_weight, mean=0.0, std=residual_std)
        nn.init.ones_(self.univariate_weight)

    def forward(self, x: torch.Tensor, post_acts: torch.Tensor):
        """
        Given the input to a KAN layer and the activation (e.g. spline(x)), compute a weighted residual.
        x has shape (bsz, in_dim) and act has shape (bsz, out_dim, in_dim)
        """
        # Broadcast the input along out_dim of post_acts
        res = self.residual_weight * self.residual_fn(x[:, None, :])
        act = self.univariate_weight * post_acts
        return res + act

有了这些用数学表示的操作，我们有足够的信息来编写一个基本的 KAN 层，方法是抽象出可学习激活 \(s_{i,j}(\cdot)\) 的选择。请注意，在下面的代码中，变量 spline_order、grid_size 和 grid_range 特定于 B-spline 作为激活，并且仅通过构造函数传递。您可以暂时忽略它们。总而言之，我们将首先计算矩阵

\begin{bmatrix} s_{1,1}(x_1), s_{1,2}(x_2), ..., s_{1,n}(x_n) \
s_{2,1}(x_1), s_{2,2}(x_2), ...,s_{2,n}(x_n) \
\vdots \
s_{m,1}(x_1), s_{m,2}(x_2), ..., s_{m,n}(x_n) \
\end{bmatrix}

然后是每个条目的加权残差，最后我们将沿行求和以获得我们的层输出。我们还定义了一个 cache() 函数来存储输入向量 \(\boldsymbol{x}\) 和 \(\Phi \boldsymbol{x}\) 矩阵，以计算稍后定义的正则化项。

class KANLayer(nn.Module):
    "Defines a KAN layer from in_dim variables to out_dim variables."
    def __init__(
        self,
        in_dim: int,
        out_dim: int,
        grid_size: int, # B-spline parameter
        spline_order: int, # B-spline parameter
        device: torch.device,
        residual_std: float = 0.1,
        grid_range: List[float] = [-1, 1], # B-spline parameter
    ):
        super(KANLayer, self).__init__()
        self.in_dim = in_dim
        self.out_dim = out_dim
        self.grid_size = grid_size
        self.spline_order = spline_order
        self.device = device

        # Define univariate function (splines in original KAN)
        self.activation_fn = KANActivation(
            in_dim,
            out_dim,
            spline_order,
            grid_size,
            device,
            grid_range,
        )
        # Define the residual connection layer used to compute \phi
        self.residual_layer = WeightedResidualLayer(in_dim, out_dim, residual_std)
        # Cache for regularization
        self.inp = torch.empty(0)
        self.activations = torch.empty(0)

    def cache(self, inp: torch.Tensor, acts: torch.Tensor):
        self.inp = inp
        self.activations = acts

    def forward(self, x: torch.Tensor):
        """
        Forward pass of KAN.
        x is expected to be of shape (bsz, in_dim) where in_dim is the number of input scalars
        and the output is of shape (bsz, out_dim).
        """
        # Compute each s_{i,j}, shape: [bsz x out_dim x in_dim]
        spline = self.activation_fn(x)
        # Form the batch of matrices phi(x) of shape [bsz x out_dim x in_dim]
        phi = self.residual_layer(x, spline)
        # Cache activations for regularization during training.
        self.cache(x, phi)
        # Really inefficient matmul
        out = torch.sum(phi, dim=-1)
        return out

KAN Learnable Activations: B-Splines

回想一下 关于 B-spline 的部分，每个激活 s_{i,j}(\cdot) 都是 G + k 个可学习系数和基函数的乘积之和 我们可以等效地将其视为两个向量之间的点积 \langle c_{i,j}, B_{i,j} (x_j) \rangle。 \(\sum_{h=1}^{G} c^{h}{i,j}, B^h{i,j} (x_j)\)，其中 G 是网格大小。 B-spline 基函数的递归定义要求我们定义网格点 (t_1,t_2,…,t_G) 以及增强的网格点 \((t_{-k},t_{-k+1},...,t_{-1},t_{G+1},....,t_{G+k})\) 在原始论文中，您可能已经注意到一个 G + k - 1 项。我在这里没有定义 t_0，并且选择不为了索引的目的而包含它，但是您基本上可以将所有内容都移动 1 来达到相同的效果。 。现在，我们将它们定义为有界区间 [low_bound, up_bound] 上的 G+1 个等大小间隔的端点 我之前提到过这一点，但是您可能会注意到，增强的网格点超出了有界域。这只是为了方便起见，但是只要它们在边界或以正确的方向在边界之外，它们是什么都没关系。您也可以只将它们设置为边界点。 但您也可以选择/学习网格点位置。最后，我们注意到，我们需要在计算每个激活 s_{i,j}(x) 时使用网格点，因此我们将其广播到 3D 张量中。

def generate_control_points(
    low_bound: float,
    up_bound: float,
    in_dim: int,
    out_dim: int,
    spline_order: int,
    grid_size: int,
    device: torch.device,
):
    """
    Generate a vector of {grid_size} equally spaced points in the interval [low_bound, up_bound]
    and broadcast (out_dim, in_dim) copies. To account for B-splines of order k, using the same spacing,
    generate an additional k points on each side of the interval. See 2.4 in original paper for details.
    """
    # vector of size [grid_size + 2 * spline_order + 1]
    spacing = (up_bound - low_bound) / grid_size
    grid = torch.arange(-spline_order, grid_size + spline_order + 1, device=device)
    grid = grid * spacing + low_bound
    # [out_dim, in_dim, G + 2k + 1]
    grid = grid[None, None, ...].expand(out_dim, in_dim, -1).contiguous()
    return grid

再次回顾一下 之前的 Cox-de Boor 递归。作为一个普遍的经验法则，我们希望避免在模型的前向传递中编写递归函数。一个常见的技巧是将我们的递归变成动态编程解决方案，我们通过以数组符号编写使其清晰： \begin{aligned} B_x[i][0] &\triangleq [x \geq t[i]] * [x < t[i+1]] \
B_{x}[i][j] &\triangleq \frac{x - t[i]}{t[i+j] - t[i]} B_{x}[i][j-1] + \frac{t[i+j+1] - x}{t[i+j+1] - t[i+1]} B_{x}[i+1][j-1] \end{aligned}

Computing the B-Spline Basis Functions

棘手的部分是用张量符号编写它 我建议您自己绘制出来。没有可视化很难解释，但推理起来很简单。 。我们利用 PyTorch/Numpy 中的广播规则在需要时复制张量。回想一下，为了实现我们的激活矩阵 \(\{s_{i,j}(x_j)\}_{i \in [m], j \in [n]}\)，我们需要计算每个激活的基，即 \