CRDTs #2: 一直都是 Semilattice(海龟理论的应用)
CRDTs #2: 一直都是 Semilattice(海龟理论的应用)
May 22, 2025 • 11 min read

在一次关于宇宙学的讲座之后,William James 受到一位怀疑论者的挑战: “你的理论是不正确的。地球 resting on a turtle。” “And what holds up the turtle?” James 问道。 “Another turtle,” 回答道。 “And what holds that up?” James 追问。 这位怀疑论者毫不气馁:“You can't fool me, sir. It’s turtles all the way down.” — Anecdote attributed to William James (via J.R. Ross, 1967)
这是我关于 CRDTs 的 4 篇系列文章的第 2 篇。请参阅介绍性文章以了解上下文。
现代分布式系统通常看起来 resting on a stack of turtles。对于我们做出的每一个保证,我们似乎都依赖于一个较低层次的假设。最终我们不禁要问:到底什么是底层的基石?
CRDTs — Conflict-Free Replicated Data Types — 经常被宣传为我们可以最终信任的基础。它们承诺跨机器的状态收敛,_而无需_完美的时钟、全局操作排序或因果消息传递……它们通过数学来实现这一点。
但是许多 CRDTs 偷偷地引入了不属于它们本身的假设。那不是坚实的基础。那不是数学。而是 turtles。
在这篇文章中,我们将展示如何正确地设计 CRDT 的内部结构:
- ✅ 始终以 semilattice 结构为基础。
- ✅ 始终采用清晰的代数推理,没有隐藏的依赖关系。
- ✅ 在需要时始终包含显式的 causality lattices。
这将确保我们始终使用谨慎的推理。
正确的 CRDTs 是底层的 semilattices。 这是你可以信赖的数学。
🐢 CRDTs 的原则:一直都是 Semilattices
每个设计良好的 CRDT 都是一个 semilattice。
- ✅ 一个 semilattice 定义了信息如何增长和
merge。 - ✅ 它通过清晰的代数,通过构造来提供收敛性。
如果你读到过关于所谓的 "state-based" 与 "op-based" CRDTs 之间的区别,你现在可以忽略它;这是一种 turtlish 分散注意力的方式,我将在下面补充说明。 重要的是:
一个 semilattice 是:
- 一组状态 SSS
- 一个
join函数 ⊔:S×S→S\sqcup : S \times S \to S⊔:S×S→S,它必须满足 commutativity,associativity 和 idempotence。
join函数会产生一个偏序:x≤y⟺x⊔y=yx \leq y \iff x \sqcup y = yx≤y⟺x⊔y=y。
在讨论 CRDTs 时,人们经常使用术语 merge 而不是 join。
CRDTs 有时会添加额外的 "update" 运算符:
update:U→(S→S): U \to (S \to S):U→(S→S)
update 接受 UUU 类型的输入值,并使用它来直接改变本地 CRDT 的状态。
如果所有节点对最终以 associative、commutative 和 idempotent 的方式 merge 状态,那么 CRDT 的最终收敛是有保证的 — 无需进一步的假设。
🔍 常见的 CRDT 错误:隐藏假设
许多 CRDT 的描述都假设因果消息传递、消息唯一性或可靠的时钟……但未能将这些编码到他们的 semilattices 中。
🚫 这就像把 turtles 再次放在 CRDT 下面!
✔️ 设计规则:
所有需要的假设必须 internalized 在 semilattice 结构中。
- 如果你的算法需要 causality,对其进行编码。
- 如果它会过期或压缩状态,也要在代数上进行建模,并确保它遵守 semilattice 的规则。
- 你总是可以在以后进行优化(参见[下面](https://jhellerstein.github.io/blog/crdt-turtles/<#building-on-an-existing-turtle>)……但数学本身必须是可靠的。
案例研究:Add/Remove Sets
让我们通过一个具体的例子。一个 2-Phase (2P) Set 是一个简单的 CRDT,它跟踪一对基于集合的 lattices (adds, removes),其中 merge 是每个集合的并集:
- adds:
{(id, element)} - removes:
{(id, timestamp)}(有时被称为 tombstones)
2P-Set 是这两个集合 lattices 的一个 free product,也就是说 2P-Set 的 merge 运算符只是 2 个 adds 集合和 2 个 removes 集合的独立 merge:
(a1,r1)⊔(a2,r2)=(a1⊔a2,b1⊔b2)(a_1, r_1) \sqcup (a_2, r_2) = (a_1 \sqcup a_2, b_1 \sqcup b_2)(a1,r1)⊔(a2,r2)=(a1⊔a2,b1⊔b2)
更新很简单:通过插入 adds 来添加一个项目,通过将它的 id 和删除时间放入 removes 来删除一个项目。 一切都很好。
直到……你尝试过期 tombstoned 数据以节省空间。
Observed-Remove (OR) Sets
OR-Set CRDT 扩展了 2P-Sets 以允许 tombstone 过期,但是……这很棘手! 让我们一起看看。
一种用于使 tombstone 过期的简单方案可能如下所示:查看本地挂钟,并从 adds 和 removes 中过期 tombstone 时间戳“旧于”阈值的 id。 事实证明,这将是不好的! 基于本地时间做出此决定可能会导致 non-convergent 行为。
这并不明显(事实上,ChatGPT 愉快地提供了两个方向上的不正确的证明!),所以我通过例子构造了一个证明。 基本思想是:即使在发出所有更新之后,节点也可以无限期地来回传递一个项目作为“hot potato”,并且尽管无限次地通信,但永远不会收敛!
单击以查看一个无限 non-convergent 的 OR-Set 循环。 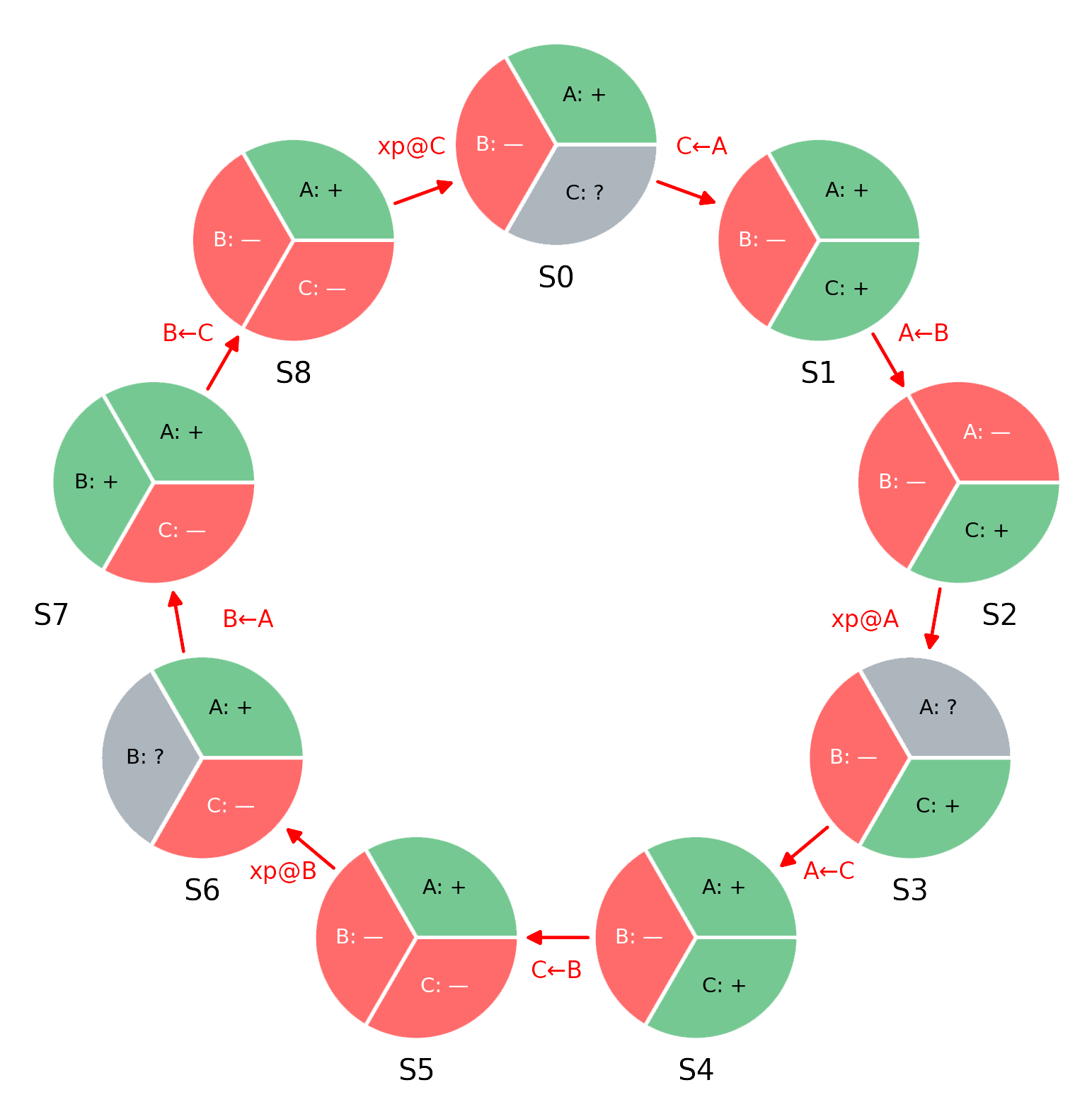
此图显示了一个振荡的状态更改周期 — 一个在 OR-set 中使用简单本地过期且永不收敛的单个项目,只是不断地从一个状态旋转到另一个状态。 每个“pie”代表该项目的 global 状态,跨三个节点 A,B 和 C。在每个状态中,每台机器要么只有在 adds 集合中(+),要么在 adds 和 removes 集合中(—),要么两者都没有(?)。 边缘标有状态转换:xp@A 表示该项目在节点 A 上过期; B <- A 表示节点 B 从节点 A 接收了该项目的一个副本。
如果需要,点击图片进行缩放。
🧯 修复:显式 Causality
这使我们回到了这篇文章的主要观点:我们需要在我们的 OR-set semilattice 中 explicitly 包含信息……在这种情况下,为了支持状态的收敛过期。 具体来说,我们可以使用嵌套的 semilattice 来跟踪 causal context — 例如 version vector — 并使用它来确定何时可以安全地过期项目:
- ✅ 仅在保证每个节点都知道 tombstone 之后才过期 tombstone。
请注意,此约束破坏了上面 non-convergence 图中的循环! 它禁止了边 S2 -> S3,S5 -> S6 和 S8 -> S0:这些边中的每一个都代表一个 tombstone 在至少一个节点处于 green + 状态且不相信该 tombstone 存在时过期!
我们通过将 OR-Set semilattice 制成一个 lexical product semilattice 来强制执行此约束:
(causalContext, (adds, removes))
与我们之前的 free product 不同,lexical product 的 merge 运算符仅在打破第一个字段 causalContext 上的 ties 时查看其第二个字段 (adds, removes):
(cC1,(a1,r1))⊔(cC2,(a2,r2))={(cC1,(a1,r1))if cC1>cC2(cC2,(a2,r2))if cC2>CC1(cC1⊔cC2,(a1⊔a2,b1⊔b2))otherwise(cC_1, (a_1, r_1)) \sqcup (cC_2, (a_2, r_2)) = \begin{cases} (cC_1, (a_1, r_1)) & \text{if } cC_1 > cC_2 \\\ (cC_2, (a_2, r_2)) & \text{if } cC_2 > CC_1 \\\ (cC_1 \sqcup cC_2, (a_1 \sqcup a_2, b_1 \sqcup b_2)) & otherwise \end{cases}(cC1,(a1,r1))⊔(cC2,(a2,r2))=⎩⎨⎧(cC1,(a1,r1))(cC2,(a2,r2))(cC1⊔cC2,(a1⊔a2,b1⊔b2))if cC1>cC2if cC2>CC1otherwise
请注意,causalContext 本身是另一个 semilattice! 它跟踪了系统范围内的哪些操作已被观察到。 这种跟踪可能是陈旧的,但它始终是保守的下限。 如果数据早于我们的 causalContext,我们可以安全地从 OR set 中过期数据。
causalContext 有不同的实现,包括 version vectors 或 causal graphs。 我们将使用 version vectors,因为它们是最常见的。
点击了解 version vectors。
我们首先确保每个节点都维护一个 local clock — 一个计数器,每次节点应用操作或发送消息时该计数器都会递增 1。 (请注意,计数器也是一个 semilattice,其中域 S=NS = \mathbb{N}S=N 是自然数 0、1、2,...,并且 merge 函数是 max。)
一个 version vector 是从 nodeId 到计数器 lattice 中的值的映射:它记录了一个节点从 每个其他节点 听说的最高时钟值。 此映射本身是一个复合 semilattice! 具体来说:
- 域 SSS 是从
nodeId(key)到 lattice (N,(\mathbb{N},(N,max)))(value)中的值的映射 merge函数只是 value latticemerge函数(即,max)的 key-wise 应用。 如果一个 key 在merge的一个输入中丢失,我们只需从另一个输入中获取它的值。
请注意我们在这里所做的事情:我们用非常简单的 semilattice 构建块形成了一个 composite semilattice (causalContext, (adds, removes))。 这些 lattices 的 merge 函数有效地递归地调用了封装的子 lattice merge 函数。
这真的是一直都是 lattices!
使用 Version Vectors 进行安全过期
要使用我们的 version vectors,我们将对我们的 OR-set 设计进行一些小的更改:
- 每个节点在本地维护一个整体 version vector,其中包含到目前为止看到的 所有 version vectors 的
merge:这通常称为 vector clock。 它代表了我们对 global 进度本地知识的高水位线。 - 当一个项目被删除时,它的 tombstone 时间戳设置为本地 vector clock。
我们现在可以安全地进行过期:只有当 tombstone 的时间戳在偏序中低于本地 vector clock 时才会过期:如果是这样,我们可以确定 每个其他节点也知道这个 tombstone,并且最终也会过期它。
关于 Op-Based CRDTs 的说明
如上所述,许多 CRDT 爱好者喜欢谈论两种“不同”的 CRDTs:正常的(“state-based”)semilattice CRDTs,以及被称为“op-based” CRDTs 的东西。 我在这里告诉你,正确的 op-based CRDTs 也是 semilattices;这种区别不是根本的。
“op-based” CRDT 只是 semilattice 的一个特定类别。 op-based CRDT 的状态表示 操作的部分排序日志(不透明命令)。 CRDT 的工作是确保部分排序的日志在节点之间是一致的。
可以通过每个站点使用 causalContext 值标记它生成的每个新 op 来捕获 ops 之间的偏序。 这确保了 (1) 来自节点 nnn 的 ops 的接收者将以与 nnn 相同的方式对它们进行排序,并且 (2) 跨 节点的操作通过 causalContext 进行因果排序。
具体来说,op-based CRDT 的状态 SSS 可以简单地是一个 (causalContext, op) 元组的 集合,其中简单的集合并集作为 merge 函数。 lattice merge 会忽略 causalContext,但将其带走以保留日志的一致偏序。 一个典型的 causalContext 实现是使用 vector clock 时间戳,每个节点为每个 op 和消息递增其在 vector clock 中的条目。
这真的是“op-based” CRDT 的全部内容:它是一个仅增长的因果标记命令集。
通常,op-based CRDT 设计假设每个站点的日志都被“播放”(积极地或懒惰地),通过以其因果偏序执行 ops 以 material 本地状态。 这仅在支持“读取”操作时才需要,因此实际上超出了 CRDT 数学的范围。 因为因果顺序只是一个偏序,所以不同的节点可以以不同的顺序“播放”一些 ops。 因此,op-based CRDT 设计通常要求 ops 本身是 mutually commutative 的。
如果一个 op-based CRDT 已经 quiescent 并传播到每个节点,并且 ops 本身是 mutually commutative 的,那么每个节点都可以“播放”一个尊重偏序的某个 total 顺序的日志,并且所有节点将最终得到一个收敛的结果。
总结一下:op-based CRDT 仍然只是一个简单的集合 semilattice! 唯一的 wrinkles 是:
- op-based CRDT 集合中的项目都带有 causalContext 的标记,以启用因果有序的重放
- 为了使 ops 在重放时有意义,跨站点的 ops 应该是 commutative 的。
🪜 你可以 Build on a Turtle — 但要知道它 Carrying 什么
有时,系统的较低层提供额外的保证,使我们可以跳过一些细节并依赖于我们下面的 turtle。
示例:如果您的网络保证因果传递,则可以安全地删除 CRDT 中的显式因果跟踪。
但请注意:您的 CRDT 现在 resting on that turtle。 如果网络实际上没有像因果 semilattice 一样运行,您的收敛证明就会失效!
📌 要点
- ✅ 每个 CRDT 必须是一个(正确的)semilattice
- ✅ 顺序比较必须尊重由
merge产生的偏序。 - ✅ 在 lattice 内部 建模所有必要的假设。
- ✅ 仅在您确切知道它们可以安全地 Carrying 什么时才 Build on trusted turtles。
当你做完这一切时?
这全是 semilattices。
那是你可以 Build on 的数学。

Joe Hellerstein
CS Prof at Berkeley.Hydro-ologist. Data drives computing.
© 2025 Joseph M. Hellerstein. All rights reserved.
